Beschreibung
Die Albers-Projektion ist eine flächentreue konische Projektion. Sie reduziert mithilfe von zwei Standardparallelen teilweise die Verzerrung einer Projektion mit nur einer Standardparallele. Die Projektion ist am besten für Landmassen geeignet, die sich bei mittleren Breitengraden von Ost nach West erstrecken. Sie wird häufig für Karten der Festlandfläche der Vereinigten Staaten, Europas und Australiens verwendet.
Die Albers-Projektion wurde 1805 von Heinrich C. Albers vorgestellt. Ellipsoidische Gleichungen wurden 1927 von Oscar S. Adams entwickelt. Sie ist in ArcGIS Pro 1.0 und höher sowie in ArcGIS Desktop 8.0.1 und höher verfügbar.
Projektionseigenschaften
In den folgenden Unterabschnitten werden die Eigenschaften der Albers-Projektion beschrieben.
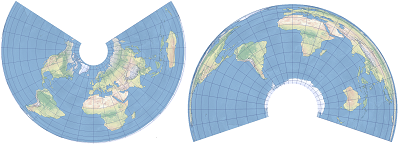
Gradnetz
Albers ist eine konische Projektion. Alle Meridiane sind gerade Linien mit gleichen Abständen, die an einem Punkt zusammenlaufen. Die Parallelen und beide Pole werden als kreisförmige Bögen dargestellt, deren Mittelpunkt der Punkt ist, an dem die Meridiane zusammentreffen. Der Abstand der Parallelen nimmt in Richtung der Pole ab. Wenn die Standardparallelen für die Nordhalbkugel festgelegt sind, ist die Fächerform des Gradnetzes nach oben ausgerichtet (dargestellt im Bild oben links). Wenn die Standardparallelen für die Südhalbkugel festgelegt sind, ist die Fächerform des Gradnetzes nach unten ausgerichtet (dargestellt im Bild oben rechts). Das Gradnetz ist über dem Mittelmeridian symmetrisch.
Verzerrung
Die Albers-Projektion ist eine flächentreue (äquivalente) Projektion. Formen, Richtungen, Winkel und Entfernungen sind im Allgemeinen verzerrt. Maßstab, Richtungen und Entfernungen stimmen nur an den Standardparallelen. Verzerrungswerte nehmen mit wachsender Entfernung von den Standardparallelen zu. Verzerrungswerte sind an einer Parallele identisch und über dem Mittelmeridian symmetrisch.
Verwendung
Diese Projektion ist am besten für die flächentreue Erstellung von Karten für Landmassen in mittleren Breitengraden geeignet, die sich von Ost nach West erstrecken, nicht von Nord nach Süd. Es empfiehlt sich, die Standardparallelen bei einem Sechstel des Breitengradbereichs unter dem oberen Rand und über dem unteren Rand der Fläche, die auf der Karte dargestellt werden soll, zu platzieren. Nach der Entwicklung von ellipsoidischen Gleichungen wurde die Projektion zum Standard für flächentreue Karten der Vereinigten Staaten.
Beschränkungen
Die Standardparallelen können an jedem Breitengrad liegen, nur nicht an gegenüber liegenden Polen.
Parameter
Die Albers-Parameter lauten wie folgt:
- Östlicher Versatz
- Nördlicher Versatz
- Mittelmeridian
- Standardparallele 1
- Standardparallele 2
- Breitengrad des Ursprungs
Besondere Parameterfälle
Wenn beide Standardparallelen auf einen Pol festgelegt sind, ist die resulierende Projektion die azimutale flächentreue Lambert-Projektion in polarer Ausrichtung. Wenn eine der Standardparallelen auf einen Pol festgelegt ist, ist das Ergebnis die konische flächentreue Lambert-Projektion. Die zylindrische flächentreue Projektion wird nur erreicht, wenn die Standardparallelen symmetrisch nördlich und südlich des Äquators festgelegt werden.
Quellen
Snyder, J. P. (1987). Map Projections: A Working Manual. US- Geological Survey Professional Paper 1395. Washington, DC: United States Government Printing Office.
Snyder, J. P. (1993). Flattening the Earth. Two Thousand Years of Map Projections. Chicago and London: University of Chicago Press.
Snyder, J. P. and Voxland, P. M. (1989). An Album of Map Projections. US- Geological Survey Professional Paper 1453. Washington, DC: United States Government Printing Office.