Mit dem Werkzeug Nachbarschaftssummenstatistik lassen sich lokale Summenstatistiken für ein oder mehrere numerische Felder in Punkt- oder Polygon-Feature mithilfe von Nachbarschaften berechnen. Zu den lokalen Statistiken gehören Mittelwert (Durchschnitt), Medianwert, Standardabweichung, Interquartil-Bereich, Schiefe und Quantil-Ungleichheit. Zu den Nachbarschaften gehören Entfernungsband, Anzahl der Nachbarn, Polygonnachbarschaft und Dateien mit räumlicher Gewichtungsmatrix. Alle lokalen Statistiken können mithilfe von Kernels geographisch gewichtet werden.
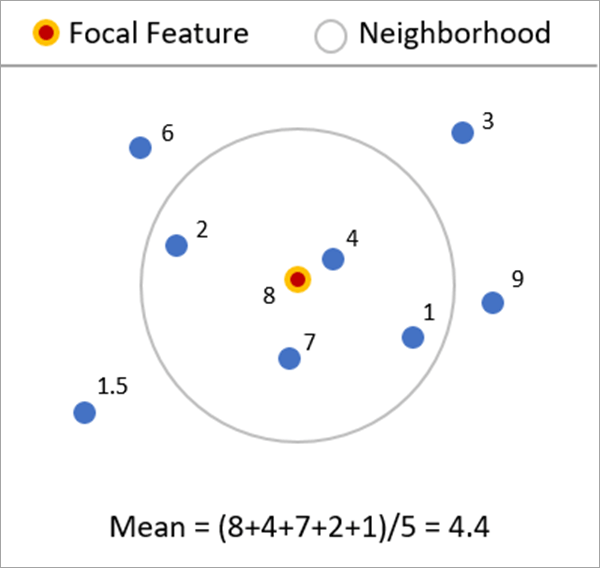
Nachbarschaftstypen
Der Parameter Nachbarschaftstyp bietet sechs Optionen zur Definition der Features, die als Nachbarn für jedes fokale Feature verwendet werden.
- Entfernungsbandband: Alle Features innerhalb einer angegeben Entfernung werden als Nachbar verwendet (maximal 1.000). Die Standardentfernung ist die kürzeste Entfernung, bei der jedes Feature mindestens einen zusätzlichen Nachbarn hat.
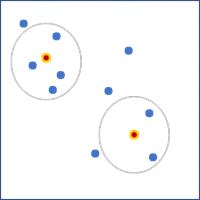
- Anzahl der Nachbarn: Eine feste Anzahl von nächstgelegenen Features, die als Nachbarn verwendet werden.
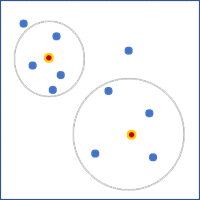
- Nur benachbarte Kanten: Polygone, die eine Kante mit dem fokalen Feature gemeinsam haben, werden als Nachbarn verwendet. Diese Option kann nur für Polygon-Features verwendet werden.
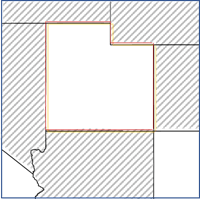
- Benachbarte Kanten/Ecken: Polygone, die eine Kante oder eine Ecke mit dem fokalen Feature gemeinsam haben, werden als Nachbarn verwendet. Diese Option kann nur für Polygon-Features verwendet werden.
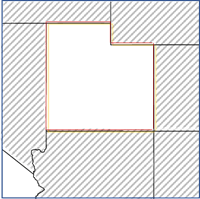
- Delaunay-Triangulation: Nachbarn werden dadurch definiert, dass sie gemeinsame Kanten oder Ecken in ihrer Delaunay-Triangulation haben. Diese Option entspricht dem Werkzeug Thiessen-Polygone erstellen für Punkte und der Option Benachbarte Kanten/Ecken für Thiessen-Polygone. Diese Option kann nur für Punkt-Features verwendet werden.
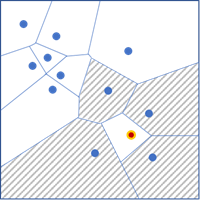
- Räumliche Gewichtungen aus Datei abrufen: Die Nachbarn und Gewichtungen alle Features werden durch eine im Parameter Gewichtungsmatrix-Datei angegebene Datei mit räumlicher Gewichtungsmatrix definiert. Sie können die Dateien mithilfe der Werkzeuge Räumliche Gewichtungsmatrix erstellen und Räumliche Gewichtung des Netzwerkes generieren erstellen.
Summenstatistik
Für jedes Analysefeld können sechs Summenstatistiken berechnet werden, diese werden mit dem Parameter Lokale Summenstatistiken angegeben. Zu den sechs Statistiken gehören Kennzahlen für die Zentralität, Kennzahlen für die Variabilität und die Streuung und Kennzahlen für die Symmetrie. Jede Klasse stellt zwei Statistiken bereit, eine traditionelle und eine robuste Variante. Auf robuste Statistiken hat eine geringe Anzahl von Ausreißern keine Auswirkung.
Standardmäßig wird die Option Alle des Parameters Lokale Summenstatistik zur Berechnung aller sechs Statistiken für die einzelnen Analysefelder verwendet. Die Formeln für die Statistiken werden im Abschnitt Formeln für lokale Statistiken aufgeführt.
Kennzahlen für die Zentralität dienen zur Schätzung des Mittelpunkts einer Verteilung von Werten. Sie können diese Optionen zum Glätten von Werten in verrauschten Daten verwenden. Die Kennzahlen für die Zentralität im Einzelnen:
- Mittelwert (traditionell): Das arithmetische Mittel (Durchschnitt) der Werte in den Analysefeldern.
- Medianwert (robust): Das 50. Perzentil der Werte des Analysefeldes. Die Hälfte der Werte liegt unterhalb und die andere Hälfte oberhalb des Medianwerts.
Kennzahlen für die Variabilität oder die Streuung dienen zum Schätzen des Bereichs der Verteilung ähnlicher Werte. Sie können mit diesem Optionen untersuchen, ob die Variabilität in den Analysefeldern auf der gesamten Karte ähnlich ist (so genannte Stationarität der Varianz) oder ob bestimmte Bereiche eine höhere lokale Variabilität aufweisen als andere. Die Kennzahlen für die Variabilität im Einzelnen:
- Standardabweichung (traditionell): Die Standardabweichung der Werte im Analysefeld.
- Interquartil-Bereich (robust): Der Bereich der mittleren 50 % der Werte im Analysefeld (zwischen dem 75. und dem 25. Perzentil). In diesen Bereich fällt die Hälfte der Daten.
Mit Kennzahlen für die Symmetrie wird gemessen, ob die Form einer Verteilung symmetrisch um den Mittelpunkt verläuft. Sie können mit diesen Optionen die Häufigkeit von hohen oder niedrigen Extremwerten untersuchen. Die Kennzahlen für die Symmetrie im Einzelnen:
- Schiefe (traditionell): Die Schiefe der Werte im Analysefeld.
- Quantil-Ungleichgewicht (robust): Ein Wert im Bereich -1 bis 1, der die Position des Medianwerts relativ zum 25. und 75. Perzentil angibt. Werte nahe -1 zeigen an, dass der Medianwert in der Nähe des 25. Perzentils liegt. Werte nahe 1 zeigen an, dass der Medianwert in der Nähe des 75. Perzentils liegt. Werte nahe 0 bedeuten Symmetrie, d. h. der Medianwert befindet sich genau in der Mitte zwischen dem 25. und dem 75. Perzentil.
Werkzeugausgaben
Die Ausgabe-Features werden in der Karte mit den im Parameter Lokale Summenstatistik angegebenen Statistiken symbolisiert; der Parameter wird für das erste bereitgestellte Analysefeld (oder für die Entfernung zu Nachbarn, wenn keine Analysefelder bereitgestellt werden) berechnet. Wenn Sie für die lokale Summenstatistik die Option Alle auswählen, enthalten die Features die Ergebnisse der Statistik Mittelwert. Die Summenstatistik für alle anderen Analysefelder werden zusammen mit Kopien aller Analysefelder als Felder in den Ausgabe-Features gespeichert. Es gibt auch Felder, die die Anzahl der für jedes Analysefeld verwendeten Nachbarn enthalten.
Geographisch gewichtete Summenstatistiken
Wenn für den Parameter Nachbarschaftstyp die Option Entfernungsband oder Anzahl der Nachbarn angegeben wurde, können alle Statistiken mit dem Parameter Lokales Gewichtungsschema geographisch gewichtet werden. Wenn Sie für den Parameter Nachbarschaftstyp die Option Räumliche Gewichtungen aus Datei abrufen angeben, werden die in der Datei festgelegten Gewichtungen als Gewichtungsschema verwendet. Wenn Sie ein Gewichtungsschema anwenden, werden alle Summenstatistiken gewichtet, sodass Nachbarn, die sich näher am fokalen Feature befinden, in eine höhere Gewichtung erhalten; diese wird mit einer so genannten Kernel-Funktion berechnet und verringert sich mit zunehmender Entfernung vom fokalen Feature. Der Parameter Lokales Gewichtungsschema stellt zwei Kernel-Funktionen bereit.
- Biquadrat
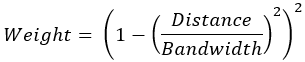
- Gauß'sche
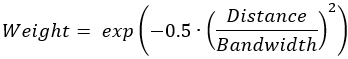
Die Kernel-Funktionen sind abhängig von einer Bandbreite, mit der gesteuert wird, wie schnell sich die Gewichtungen mit zunehmender Entfernung verringern. Die Bandbreite für jede Kernel-Funktion wird im Parameter Kernel-Bandbreite bereitgestellt. Wenn Sie hier keinen Wert angeben, wird zur Laufzeit ein Standardwert geschätzt und als Geoverarbeitungsmeldung angezeigt. Weitere Informationen über die Berechnung der Standardbandbreite finden Sie unter Funktionsweise von "Kerndichte".
Hinweis:
Beim Nachbarschaftstyp "Entfernungsband" entspricht der Standardwert der Kernel-Bandbreite dem Wert des Parameters Entfernungsband.
Formeln für lokale Statistiken
In diesem Abschnitt werden die Formeln für die gewichteten und ungewichteten Versionen aller Summenstatistiken für ein einzelnes fokales Feature vorgestellt. Die Formeln werden für alle Analysefelder auf jedes Eingabe-Feature angewendet.
In allen Formeln sind i = 1, ..., n Nachbarn des fokalen Features (möglicherweise einschließlich des Features selbst); sie sind aufsteigend nach Wert sortiert (xi). Alle Gewichtungen (wi) werden vor Anwendung der Formel auf 1 normalisiert. Die ungewichteten Versionen aller Statistiken werden durch die folgende Einstellung abgeleitet: wi = 1/n für alle Nachbarn i.
Traditionelle Statistiken
Die folgende Tabelle zeigt die gewichteten und ungewichteten Versionen aller traditionellen Summenstatistiken.
| Statistiken | Gewichtete Formel | Ungewichtete Formel |
|---|---|---|
Mittelwert | 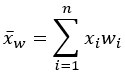 | 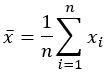 |
Standardabweichung | 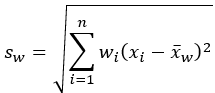 | 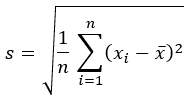 |
Schiefe | 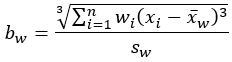 | 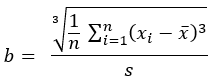 |
Robuste Statistiken
Alle robusten Statistiken hängen von der Definition eines gewichteten p-Quantils ab, wobei p zwischen 0 und 1 liegt. Diese Definition wird für die Berechnung des gewichteten Medianwerts (p=0,5), des gewichteten ersten Quartils (p=0,25) und des gewichteten dritten Quartils (p=0,75) verwendet. Das p-Quantil für einen gegebenen Wert p wird wie folgt definiert:
- Gewichtetes p-Quantil:
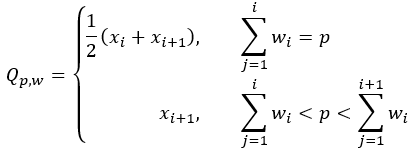
- Ungewichtetes p-Quantil:
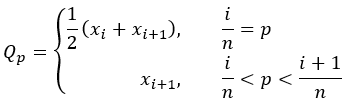
Auf der Grundlage der obigen Definition des p-Quantils zeigt die folgende Tabelle die gewichtete und ungewichtete Version der einzelnen robusten Summenstatistiken.
| Statistiken | Gewichtete Formel | Ungewichtete Formel |
|---|---|---|
Medianwert | 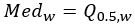 | 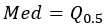 |
Interquartil-Bereich | 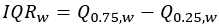 | 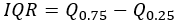 |
Quantil-Ungleichgewicht | 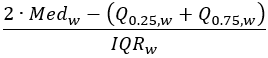 | 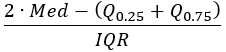 |
Zusätzliche Ressourcen
Weitere Informationen über geographisch gewichtete Summenstatistiken finden Sie in der folgenden Referenzliteratur:
- Brunsdon, C., Fotheringham, A.S., Charlton, M. (2002). "Geographically weighted summary statistics — a framework for localised exploratory data analysis." Computers, Environment and Urban Systems, 26(6), 501-524. ISSN 0198-9715. https://doi.org/10.1016/S0198-9715(01)00009-6.