Beim Werkzeug Geographisch gewichtete Regression kommt die geographisch gewichtete Regression (GWR) zum Einsatz. Es handelt sich um eine von mehreren räumlichen Regressionstechniken, die in der Geographie und anderen Disziplinen eingesetzt werden. Sie dient zur Auswertung eines lokalen Modells der Variablen oder des Prozesses, die bzw. den Sie verstehen oder vorhersagen möchten, indem eine Regressionsgleichung an jedes Feature im Dataset angepasst wird. Diese separaten Gleichungen werden durch Einbeziehung der abhängigen und erklärenden Variablen von Features in der Nachbarschaft der einzelnen Ziel-Features erstellt. Bei Verwendung des Werkzeugs Geographisch gewichtete Regression basieren Form und Ausdehnung jeder analysierten Nachbarschaft auf den Werten der Parameter Nachbarschaftstyp und Auswahlmethode für Nachbarschaften. Als abhängige Variable für das Werkzeug sind kontinuierliche Daten (Gauß), binäre Daten (binomial) sowie Anzahldaten (Poisson) zulässig. Wenden Sie die GWR auf Datasets mit mindestens mehreren hundert Features an.
Hinweis:
Das Werkzeug Geographisch gewichtete Regression (Multiscale) kann verwendet werden, um GWR für Daten mit unterschiedlichen Maßstäben von Beziehungen zwischen den abhängigen und erklärenden Variablen durchzuführen.
Potenzielle Anwendungsbereiche
Das Werkzeug Geographisch gewichtete Regression kann zur Beantwortung verschiedener Fragen herangezogen werden, darunter die folgenden:
- Ist die Beziehung zwischen Bildungsabschluss und Einkommen im gesamten Untersuchungsgebiet konsistent?
- Treten bestimmte Krankheitsfälle in der Nähe von Wasserflächen häufiger auf?
- Was sind die Hauptvariablen, die eine hohe Waldbrandhäufigkeit erklären?
- Welche Lebensräume sollten geschützt werden, um die Wiedereinführung einer gefährdeten Spezies zu fördern?
- In welchen Bezirken erzielen Kinder gute Ergebnisse bei Leistungstests? Welche Eigenschaften scheinen verknüpft zu sein? Wo sind die einzelnen Eigenschaften am wichtigsten?
- Sind die Faktoren, die höhere Krebsraten beeinflussen, im gesamten Untersuchungsgebiet konsistent?
Eingaben
Um das Werkzeug Geographisch gewichtete Regression auszuführen, geben Sie im Parameter Eingabe-Features ein Feld an, das die abhängige Variable darstellt, sowie ein oder mehrere Felder, die die erklärenden Variablen darstellen. Diese Felder müssen numerisch sein und einen Wertebereich aufweisen. Features, bei denen Werte in der abhängigen oder erklärenden Variablen fehlen, werden von der Analyse ausgeschlossen. Sie können jedoch mit dem Werkzeug Fehlende Werte ausfüllen das Dataset vervollständigen, bevor Sie das Werkzeug Geographisch gewichtete Regression ausführen. Als Nächstes müssen Sie auf der Basis der zu analysierenden Daten einen Modelltyp auswählen. Es ist wichtig, ein für die Daten geeignetes Modell zu verwenden. Im Folgenden werden die Modelltypen beschrieben, und Sie erfahren, wie Sie das geeignete Modell für die Daten ermitteln können.
Modelltypen
Das Werkzeug Geographisch gewichtete Regression stellt drei Typen von Regressionsmodellen bereit: kontinuierlich, binär und Anzahl. Diese Regressionstypen werden als Regression der kleinsten Quadrate (Ordinary Least Squares), logistische Regression und Poisson-Regression bezeichnet. Der Wert des Parameters Modelltyp muss für die Analyse darauf basieren, wie die abhängige Variable gemessen oder zusammengefasst wurde und welchen Wertebereich sie umfasst.
Kontinuierlich (Gauß)
Verwenden Sie die Option Kontinuierlich (Gauß), wenn die abhängige Variable einen großen Wertebereich haben kann, z. B. Temperaturen oder Umsätze. Im Idealfall ist die abhängige Variable normal verteilt. Sie können für die abhängige Variable ein Histogramm erstellen, um zu überprüfen, ob es normal verteilt ist. Ist das Histogramm eine symmetrische Glockenkurve, verwenden Sie den Gauß-Modelltyp. Die meisten Werte bilden ein Cluster in der Nähe des Mittelwerts, und es gibt nur wenige Werte, die stark vom Mittelwert abweichen. Auf der linken Seite des Mittelwerts sollten sich ebenso viele Werte befinden wie auf der rechten Seite (Mittel- und Medianwert sind für die Verteilung identisch). Wenn die abhängige Variable nicht normal verteilt ist, haben Sie die Möglichkeit, diese als binäre Variable zu reklassifizieren. Ist die abhängige Variable beispielsweise das durchschnittliche Haushaltseinkommen, können Sie diese in eine binäre Variable umcodieren, wobei 1 angibt, dass der Wert über dem nationalen Durchschnitt liegt, und 0 (Null), dass er unter dem Durchschnitt liegt. Sie können ein kontinuierliches Feld mit der Hilfsfunktion Reklassifizieren des Werkzeugs Feld berechnen als binäres Feld reklassifizieren.
Binär (Logistisch)
Verwenden Sie die Option Binär (Logistisch), wenn die abhängige Variable einen von zwei möglichen Werten annehmen kann, z. B. Erfolg oder Misserfolg, Anwesenheit oder Abwesenheit. Bei dem Feld mit der abhängigen Variable muss es sich um ein numerisches Feld handeln, das nur Einsen und Nullen enthält. Die Ergebnisse lassen sich einfacher interpretieren, wenn Sie das relevante Ereignis, z. B. Erfolg oder die Anwesenheit eines Tieres, als 1 codieren, da die Regression die Wahrscheinlichkeit von 1 modelliert. Sowohl global als auch lokal sollten die Einsen und Nullen in den Daten variieren. Mit dem Werkzeug Nachbarschaftssummenstatistik können Sie Standardabweichungen von lokalen Nachbarschaften berechnen, um Bereiche zu bestimmen, die alle denselben Wert besitzen.
Anzahl (Poisson)
Verwenden Sie die Option Anzahl (Poisson), wenn die abhängige Variable diskontinuierlich ist und die Anzahl eines bestimmten Ereignisses darstellt, z. B. die Anzahl von Straftaten. Anzahlmodelle können auch verwendet werden, wenn die abhängige Variable ein Verhältnis darstellt und es sich bei dem Nenner des Verhältnisses um einen Festwert handelt, z. B. Umsatz pro Monat oder die Anzahl der krebskranken Personen pro 10.000 Einwohner. Die Werte der abhängigen Variable dürfen nicht negativ sein oder Dezimalstellen enthalten.
Nachbarschaftstypen
Eine Nachbarschaft ist das Entfernungsband oder die Anzahl der Nachbarn, das bzw. die für jede lokale Regressionsgleichung verwendet wird. Es handelt sich um den vielleicht wichtigsten Parameter, der beim Werkzeug Geographisch gewichtete Regression berücksichtigt werden sollte, da er den Lokalitätsgrad für die Modellschätzung steuert. Form und Ausdehnung der analysierten Nachbarschaften basieren auf den Werten der Parameter Nachbarschaftstyp und Auswahlmethode für Nachbarschaften.
Sie haben die Wahl zwischen zwei Nachbarschaftstypen: eine feste Anzahl an Nachbarn oder ein Entfernungsband. Bei einer festen Anzahl an Nachbarn hängt die Fläche der Nachbarschaft von der Dichte nahe gelegener Punkte ab: Nachbarschaften sind kleiner, wenn die Features dicht beieinander liegen, und größer, wenn die Features weit auseinander liegen. Wird ein Entfernungsband verwendet, bleibt die Nachbarschaftsgröße für jedes Feature im Untersuchungsgebiet konstant. Dies führt zu mehr Features pro Nachbarschaft, wenn die Features dicht sind, und weniger Features pro Nachbarschaft, wenn diese spärlich vorhanden sind.
Die Auswahlmethode für Nachbarschaften gibt an, wie die Größe der Nachbarschaft bestimmt wird (die tatsächliche Entfernung oder die Anzahl an verwendeten Nachbarn). Die mit der Option Golden Search oder Manuelle Intervalle ausgewählten Nachbarschaften basieren auf der Minimierung des Wertes für das korrigierte Akaike Information Criterion (AICc). Alternativ können Sie mit der Option Benutzerdefiniert eine bestimmte Nachbarschaftsentfernung oder Anzahl der Nachbarn festlegen.
Bei der Auswahlmethode Golden Search ermittelt das Werkzeug mit dem Suchverfahren "Golden Section Search" die besten Werte für das Entfernungsband oder die Anzahl der Nachbarn. Bei dieser Methode werden zunächst die Maximal- und Minimalentfernungen bestimmt; dazwischen wird inkrementell das AICc mit verschiedenen Entfernungen gemessen. Die maximale Entfernung ist die Entfernung, bei der jedes Feature die Hälfte der Anzahl an Eingabe-Features als Nachbarn aufweist; die minimale Entfernung ist die Entfernung, bei der jedes Feature mindestens 5 Prozent der Features im Dataset als Nachbarn aufweist.
Mit den Parametern Minimale Suchentfernung und Maximale Suchentfernung (für Entfernungsband) sowie Minimale Anzahl von Nachbarn und Maximale Anzahl von Nachbarn (für Anzahl der Nachbarn) kann der Suchbereich der Golden Search begrenzt werden.
Hinweis:
Wenn die Nachbarschaftsparameter mehr als 1.000 Nachbarn für eine Nachbarschaft ergeben, werden nur die 1.000 nächstgelegenen Nachbarn verwendet.
Lokales Gewichtungsschema
Der große Vorteil der GWR besteht darin, dass auf die in jeder lokalen Regressionsgleichung verwendeten Features eine geographische Gewichtung angewendet wird. Features, die weiter vom Regressionspunkt entfernt sind, erhalten eine geringere Gewichtung und haben weniger Einfluss auf die Regressionsergebnisse für das Ziel-Feature; Features, die näher daran liegen, haben in der Regressionsgleichung eine höhere Gewichtung. Die Gewichtung wird mithilfe eines Kernels ermittelt. Dies ist eine Funktion, die bestimmt, wie schnell die Gewichtung mit zunehmender Entfernung abnimmt. Das Werkzeug Geographisch gewichtete Regression bietet zwei Kernel-Optionen für den Parameter Lokales Gewichtungsschema: Gauß und Biquadrat.
Das Gauß-Gewichtungsschema weist dem fokalen Feature eine Gewichtung von 1 zu, wobei die Gewichtungen für die benachbarten Features mit zunehmender Entfernung vom fokalen Feature allmählich abnimmt. Liegen zwei Features beispielsweise 0,25 Bandbreiten auseinander, beträgt die daraus resultierende Gewichtung in der Gleichung etwa 0,88. Liegen die Features 0,75 Bandbreiten auseinander, beträgt die daraus resultierende Gewichtung etwa 0,32. Ein Gauß-Gewichtungsschema erreicht nie Null, aber die Gewichtungen für Features, die sehr weit von der Regressionsfunktion entfernt sind, können so klein sein, dass sie praktisch keinen Einfluss auf die Regression haben. Bei Verwendung eines Gauß-Gewichtungsschemas gelten alle anderen Features in den Eingabedaten als benachbarte Features und erhalten deshalb eine Gewichtung. Überschreitet die Anzahl der benachbarten Features jedoch 1000, werden aus Gründen der Recheneffizienz nur die nächsten 1000 in jede lokale Regression aufgenommen. Ein Gauß-Gewichtungsschema stellt sicher, dass jedes Regressions-Feature zahlreiche Nachbarn aufweist, und erhöht die Wahrscheinlichkeit, dass die Werte dieser Nachbarn ausreichend variieren. Auf diese Weise kann ein häufiges Problem der geographisch gewichteten Regression, die so genannte lokale Kollinearität, vermieden werden. Verwenden Sie ein Gauß-Gewichtungsschema, wenn der Einfluss benachbarter Features gleichmäßig und allmählich abnimmt, aber immer vorhanden ist, unabhängig davon, wie weit entfernt die umliegenden Features sind.
Das Gewichtungsschema "Biquadrat" ähnelt dem Gauß-Gewichtungsschema. Es weist dem fokalen Feature eine Gewichtung von 1 zu, wobei die Gewichtungen für die benachbarten Features mit zunehmender Entfernung vom fokalen Feature allmählich abnehmen. Allerdings wird allen Features außerhalb der angegebenen Nachbarschaft die Gewichtung 0 zugewiesen, sodass sie keinen Einfluss auf die lokale Regression für das Ziel-Feature haben. Im Vergleich zu einem Gauß-Gewichtungsschema nehmen die Gewichtungen in einem Biquadrat-Gewichtungsschema mit den gleichen Nachbarschaftsspezifikationen schneller ab. Mit einem Biquadrat-Gewichtungsschema können Sie eine Entfernung angeben, ab der Features keinen Einfluss auf die Regressionsergebnisse mehr haben. Da das Biquadrat-Schema Features ab einer bestimmten Entfernung ausschließt, gibt es keine Garantie, dass genügend Features (bzw. Features mit Einfluss) in der Nachbarschaft vorhanden sind, um eine zuverlässige lokale Regressionsanalyse durchzuführen. Verwenden Sie ein Gauß-Gewichtungsschema, wenn der Einfluss der benachbarten Features allmählich abnimmt und es eine Entfernung gibt, ab der sich dieser Einfluss nicht mehr auswirkt. Beispielsweise wird die Regression häufig zur Modellierung von Immobilienpreisen verwendet, und der Verkaufspreis der umliegenden Häuser ist eine oft verwendete erklärende Variable. Diese umliegenden Häuser werden als Vergleichsobjekte bezeichnet. Kreditinstitute haben zuweilen Regeln, die besagen, dass sich ein vergleichbares Haus innerhalb einer bestimmten Entfernung befinden muss. In diesem Fall kann ein Biquadrat-Gewichtungsschema mit einer Nachbarschaft verwendet werden, die der vom Kreditinstitut vorgegebenen maximalen Entfernung entspricht.
Vorhersage
Mit dem erstellten Regressionsmodell können Sie Vorhersagen für andere Features (Punkte oder Polygone) im selben Untersuchungsgebiet treffen. Geben Sie dazu die Features im Parameter Vorherzusagende Positionen an. Für jede erklärende Variable der Eingabe-Features müssen die vorherzusagenden Positionen übereinstimmende Felder aufweisen. Wenn die Feldnamen der Eingabe-Features und der vorherzusagenden Positionen nicht übereinstimmen, müssen Sie die entsprechenden Felder im Parameter Abzugleichende erklärende Variablen abgleichen. Beim Abgleich müssen die Felder denselben Typ aufweisen (z. B. können Felder vom Typ "Double" nicht mit Feldern vom Typ "Integer" abgeglichen werden).
Koeffizienten-Raster
Im Vergleich zu den meisten Regressionsmodellen ist ein Hauptvorteil der GWR, dass sie es Ihnen ermöglicht, räumlich variierende Beziehungen zu untersuchen. Eine Möglichkeit, wie Sie die variierenden Beziehungen zwischen den erklärenden Variablen und der abhängigen Variablen im Raum visualisieren können, besteht darin, Koeffizienten-Raster zu erstellen. Wenn Sie einen Pfadnamen als Wert für den Parameter Koeffizienten-Raster-Workspace angeben, erstellt das Werkzeug Geographisch gewichtete Regression Koeffizienten-Raster-Oberflächen für das Modell-Intercept und jede erklärende Variable. Die Auflösung der Raster wird mithilfe der Umgebung Zellengröße gesteuert. Eine Nachbarschaft wird basierend auf dem Nachbarschaftstyp und dem Gewichtungsschema um die einzelnen Raster-Zellen herum konstruiert. Ausgehend von der Mitte der Raster-Zelle werden bis zu allen Eingabe-Features, die innerhalb der Nachbarschaft liegen, Gewichtungen berechnet. Diese werden zur Berechnung einer eindeutigen Regressionsgleichung für die jeweilige Raster-Zelle verwendet. Die Koeffizienten variieren von Raster-Zelle zu Raster-Zelle, da sich die Nachbarn und Gewichtungen von Zelle zu Zelle ändern.
Hinweis:
Es herrscht aktuell kein Konsens darüber, wie das Vertrauen in die Koeffizienten aus einem GWR-Modell zu bewerten ist. Zwar wurden t-Tests durchgeführt, um einen Rückschluss darauf zu ermöglichen, ob der geschätzte Wert der Koeffizienten signifikant von Null abweicht, aber die Gültigkeit dieses Ansatzes ist derzeit noch Gegenstand der aktiven Forschung. Ein Ansatz zur informellen Bewertung der Koeffizienten besteht darin, den Koeffizienten durch den für jedes Feature angegebenen Standardfehler zu dividieren, um den Umfang der Schätzung mit dem verbundenen Standardfehler zu skalieren. Diese Ergebnisse können dann visualisiert werden, um nach Clustern mit hohen Standardfehlern relativ zu ihren Koeffizienten zu suchen.
Ausgaben
Das Werkzeug Geographisch gewichtete Regression erzeugt verschiedene Ausgaben. Eine Zusammenfassung des GWR-Modells sowie statistische Zusammenfassungen werden als Meldungen zurückgegeben. Darüber hinaus generiert das Werkzeug eine Ausgabe-Feature-Class, Diagramme sowie optional Vorhersage-Features und Koeffizienten-Raster-Oberflächen. Die Ausgabe-Features sowie verknüpfte Diagramme werden automatisch dem Bereich Inhalt hinzugefügt, wobei ein Hot/Cold-Rendering-Schema zur Modellierung von Residuen angewendet wird. Die generierten Diagnosen und Diagramme sind abhängig vom angegebenen Modelltyp.
Kontinuierlich (Gauß)
Beim Gauß'schen Modelltyp wird davon ausgegangen, dass die Werte der abhängigen Variable kontinuierlich sind.
Ausgabe-Features
Neben Regressionsresiduen umfassen die Ausgabe-Features Felder für beobachtete und vorhergesagte abhängige Variablenwerte, den Bedingungswert, den lokalen R-Squared-Wert, erklärende Variablenkoeffizienten und Standardfehler. In einer Karte werden die Ausgabe-Features als Layer hinzugefügt und basierend auf den standardisierten Residuen symbolisiert. Ein positives standardisiertes Residuum bedeutet, dass der Wert der abhängigen Variable größer ist als der vorhergesagte Wert (Unterschätzung), und ein negatives standardisiertes Residuum bedeutet, dass der Wert kleiner ist als der vorhergesagte Wert (Überschätzung).
Es werden ebenfalls die Werte für Schnittpunkt, Standardfehler des Schnittpunktes, Koeffizienten, Standardfehler für jede der erklärenden Variablen, vorhergesagter Wert, Residuum, standardisiertes Residuum, Einfluss, Cook'sche Distanz, lokaler R-Squared-Wert und Bedingungswert gemeldet. Viele dieser Felder werden unter Funktionsweise der OLS-Regression erläutert. Die Werte für Einfluss und Cook'sche Distanz messen beide den Einfluss des Features auf die Schätzung der Regressionskoeffizienten. Sie können ein Histogramm verwenden, um zu ermitteln, ob wenige Features mehr Einfluss haben als der Rest des Datasets. Diese Features sind häufig Ausreißer, die die Schätzung der Koeffizienten verzerren. Die Modellergebnisse können besser werden, wenn sie entfernt werden und das Werkzeug erneut ausgeführt wird. Der lokale R-Squared-Wert liegt zwischen 0 und 1 und stellt die Stärke der Korrelationen des lokalen Modells des Features dar. Der Bedingungswert ist ein Maß für die Stabilität der geschätzten Koeffizienten. Bedingungswerte über etwa 1000 kennzeichnen eine Instabilität im Modell. Häufig wird sie durch erklärende Variablen verursacht, die eng korrelieren.
Interpretieren von Meldungen und Diagnosen
Die Meldungen enthalten Analysedetails, einschließlich der Anzahl der analysierten Features, der abhängigen und erklärenden Variablen und der Anzahl der angegebenen Nachbarn. Darüber hinaus werden verschiedene Modelldiagnosen gemeldet.
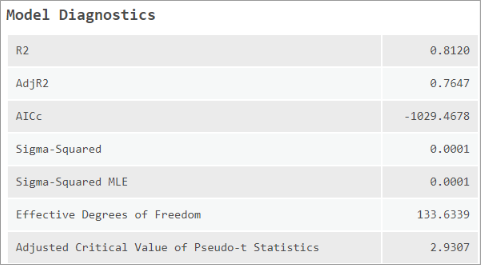
- R2: R-Squared ist ein Maß für die Anpassungsgüte. Der Wert variiert von 0.0 bis 1.0, wobei höhere Werte vorzuziehen sind. Er kann als Anteil der abhängigen Variablenvarianz durch das Regressionsmodell interpretiert werden. Der Nenner für die Berechnung von R2 ist die Summe von abhängigen Variablenwerten im Quadrat. Durch Hinzufügen einer zusätzlichen erklärenden Variable zum Modell wird nicht der Nenner, sondern der Zähler geändert; dadurch entsteht der Eindruck, dass die Modelleignung verbessert wird, was aber möglicherweise nicht der Fall ist. Weitere Informationen finden Sie nachfolgend unter "AdjR2".
- AdjR2: Aufgrund des oben beschriebenen Problems mit dem R2-Wert werden durch Berechnungen des Wertes "Adjusted R-Squared" der Zähler und der Nenner nach ihren Freiheitsgraden normalisiert. Dadurch wird die Anzahl der Variablen in einem Modell ausgeglichen, und folglich ist der angepasste R2-Wert (Adjusted R2) fast immer kleiner als der R2-Wert. Indem Sie diese Anpassung vornehmen, geht jedoch die Interpretation des Werts als Anteil der erläuterten Varianz verloren. Bei der GWR ist die effektive Anzahl von Freiheitsgraden eine Funktion der verwendeten Nachbarschaft, sodass die Anpassung im Vergleich zu einem globalen Modell, wie es im Werkzeug Generalisierte lineare Regression Verwendung findet, möglicherweise stark ausgeprägt. Aus diesem Grund wird AICc zum Vergleichen von Modellen vorgezogen.
- AICc: Hierbei handelt es sich um einen Messwert für die Modell-Performance, der verwendet werden kann, um Regressionsmodelle zu vergleichen. Unter Berücksichtigung der Modellkomplexität bietet das Modell mit dem niedrigeren AICc-Wert eine bessere Übereinstimmung mit den beobachteten Daten. AICc ist kein absolutes Maß für die Anpassungsgüte, ist aber hilfreich für das Vergleichen von Modellen mit unterschiedlichen erklärenden Variablen, solange sie die gleiche abhängige Variable betreffen. Wenn sich die AICc-Werte für zwei Modelle um mehr als 3 unterscheiden, wird das Modell mit dem niedrigeren AICc-Wert als besser betrachtet. Indem Sie den AICc-Wert aus der GWR mit dem AICc-Wert aus der generalisierten linearen Regression (GLR) vergleichen, können Sie beurteilen, ob der Umstieg von einem globalen Modell (GLR) auf ein lokales Regressionsmodell (GWR) von Vorteil ist.
Unter Gollini et al. im Abschnitt Zusätzliche Quellen finden Sie die Formeln, die zum Berechnen der AICc-Werte für alle Modelltypen verwendet wurden.
- Sigma-Squared: Dies ist die Least-Squares-Schätzung der Varianz (Quadrat der Standardabweichung) für die Residuen. Kleinere Werte dieser Statistik sind vorzuziehen. Dieser Wert ist die normalisierte Residuenquadratsumme, wobei die Residuenquadratsumme durch die effektiven Freiheitsgrade der Residuen dividiert wird. Sigma-Squared wird für AICc-Berechnungen verwendet.
- Sigma-Squared – MLE: Dies ist die Maximum-Likelihood-Schätzung (Maximum Likelihood Estimate, MLE) der Varianz (Quadrat der Standardabweichung) für die Residuen. Kleinere Werte dieser Statistik sind vorzuziehen. Zur Berechnung dieses Wertes wird die Restsumme von Quadraten durch die Anzahl der Eingabe-Features dividiert.
- Effektive Freiheitsgrade: Dieser Wert spiegelt einen Kompromiss zwischen der Varianz der angepassten Werte und der Verzerrung in den Koeffizientenschätzungen wider und steht im Zusammenhang mit der ausgewählten Nachbarschaftsgröße. Da sich die Nachbarschaft der Unendlichkeit nähert, nähern sich die geographischen Gewichtungen für jedes Feature dem Wert 1, und die Koeffizientenschätzungen liegen sehr nah an den Schätzungen für ein globales GLR-Modell. Bei sehr großen Nachbarschaften nähert sich die effektive Anzahl von Koeffizienten der tatsächlichen Anzahl. Lokale Koeffizientenschätzungen weisen eine kleine Varianz auf, sind aber verzerrt. Umgekehrt nähern sich die geographischen Gewichtungen für jedes Feature dem Wert 0, wenn die Nachbarschaft kleiner wird und sich 0 nähert, mit Ausnahme des Regressionspunktes. Bei sehr kleinen Nachbarschaften entspricht die effektive Anzahl der Koeffizienten der Anzahl der Beobachtungen. Lokale Koeffizientenschätzungen weisen eine große Varianz, jedoch nur eine geringe Verzerrung auf. Die effektive Anzahl wird verwendet, um zahlreiche andere Diagnosemessungen zu berechnen.
- Angepasster kritischer Wert von Pseudo-T-Statistiken: Dies ist der angepasste kritische Wert, mit dem die statistische Signifikanz der Koeffizienten in einem zweiseitigen T-Test mit einer Konfidenz von 95 Prozent getestet werden. Der Wert entspricht einem Signifikanzniveau (Alpha) von 0,05 geteilt durch die effektiven Freiheitsgrade. Diese Anpassung steuert die familienweise Fehlerrate (FWER) der Signifikanz der erklärenden Variablen.
Ausgabediagramme
Dieses Werkzeug gibt im Bereich Inhalt eine Scatterplotmatrix und ein Histogramm aus. Die Scatterplotmatrix enthält eine abhängige Variable und bis zu 9 erklärende Variablen. Im Histogramm werden das abweichende Residuum und eine Normalverteilungskurve angezeigt.
Binär (Logistisch)
Beim binären Modelltyp wird davon ausgegangen, dass es sich bei den Werten der abhängigen Variable um Binärwerte (0 oder 1) handelt.
Feature-Class und hinzugefügte Felder
Die Ausgabe-Features enthalten Felder für den Schnittpunkt (INTERCEPT), den Standardfehler des Schnittpunktes (SE_INTERCEPT), die Koeffizienten und die Standardfehler jeder erklärenden Variablen. Zudem werden die Wahrscheinlichkeit, dass es sich um den Wert 1 handelt, der vorhergesagte Wert, das abweichende Residuum, GInfluence und die lokale prozentuale Abweichung angegeben.
Interpretieren von Meldungen und Diagnosen
Die Meldungen enthalten Analysedetails, einschließlich der Anzahl der analysierten Features, der abhängigen und erklärenden Variablen und der Anzahl der angegebenen Nachbarn. Darüber hinaus werden die folgenden Diagnosen gemeldet:
- % Abweichung, die durch das globale Modell (nicht räumlich) erklärt wird: Dies ist ein Maß für die Anpassungsgüte, das die Performance eines globalen Modells (GLR) quantifiziert. Der Wert variiert von 0.0 bis 1.0, wobei höhere Werte vorzuziehen sind. Er kann als Anteil der abhängigen Variablenvarianz durch das Regressionsmodell interpretiert werden.
- % Abweichung, die durch das lokale Modell erklärt wird: Dies ist ein Maß für die Anpassungsgüte, das die Performance eines lokalen Modells (GWR) quantifiziert. Der Wert variiert von 0.0 bis 1.0, wobei höhere Werte vorzuziehen sind. Er kann als Anteil der abhängigen Variablenvarianz durch das lokale Regressionsmodell interpretiert werden.
- % Abweichung, die durch das lokale im Vergleich zum globalen Modell erklärt wird: Dieser Anteil ist eine Möglichkeit, die Vorteile des Umstiegs von einem globalen Modell (GLR) auf ein lokales Regressionsmodell (GWR) zu beurteilen, indem die Restsumme von Quadraten des lokalen Modells mit der Restsumme von Quadraten des globalen Modells verglichen wird. Der Wert variiert von 0,0 bis 1,0, wobei höhere Werte angeben, dass das lokale Regressionsmodell besser abgeschnitten hat als ein globales Modell.
- AICc: Hierbei handelt es sich um einen Messwert für die Modell-Performance, der verwendet werden kann, um Regressionsmodelle zu vergleichen. Unter Berücksichtigung der Modellkomplexität bietet das Modell mit dem niedrigeren AICc-Wert eine bessere Übereinstimmung mit den beobachteten Daten. AICc ist kein absolutes Maß für die Anpassungsgüte, ist aber hilfreich für das Vergleichen von Modellen mit unterschiedlichen erklärenden Variablen, solange sie die gleiche abhängige Variable betreffen. Wenn sich die AICc-Werte für zwei Modelle um mehr als 3 unterscheiden, wird das Modell mit dem niedrigeren AICc-Wert als besser betrachtet. Indem Sie den AICc-Wert aus der GWR mit dem AICc-Wert aus der Kleinste-Quadrate-Methode (Ordinary Least Squares, OLS) vergleichen, können Sie beurteilen, ob der Umstieg von einem globalen Modell (OLS) auf ein lokales Regressionsmodell (GWR) von Vorteil ist.
- Sigma-Squared: Dieser Wert ist die normalisierte Residuenquadratsumme, wobei die Residuenquadratsumme durch die effektiven Freiheitsgrade des Residuums dividiert wird. Dies ist die Least-Squares-Schätzung der Varianz (Quadrat der Standardabweichung) für die Residuen. Kleinere Werte dieser Statistik sind vorzuziehen. Sigma-Squared wird für AICc-Berechnungen verwendet.
- Sigma-Squared – MLE: Dies ist die Maximum-Likelihood-Schätzung (Maximum Likelihood Estimate, MLE) der Varianz (Quadrat der Standardabweichung) für die Residuen. Kleinere Werte dieser Statistik sind vorzuziehen. Zur Berechnung dieses Wertes wird die Restsumme von Quadraten durch die Anzahl der Eingabe-Features dividiert.
- Effektive Freiheitsgrade: Dieser Wert spiegelt einen Kompromiss zwischen der Varianz der angepassten Werte und der Verzerrung in den Koeffizientenschätzungen wider und steht im Zusammenhang mit der ausgewählten Nachbarschaftsgröße. Da sich die Nachbarschaft der Unendlichkeit nähert, nähern sich die geographischen Gewichtungen für jedes Feature dem Wert 1, und die Koeffizientenschätzungen liegen sehr nah an den Schätzungen für ein globales GLR-Modell. Bei sehr großen Nachbarschaften nähert sich die effektive Anzahl von Koeffizienten der tatsächlichen Anzahl. Lokale Koeffizientenschätzungen weisen eine kleine Varianz auf, sind aber verzerrt. Umgekehrt nähern sich die geographischen Gewichtungen für jedes Feature dem Wert 0, wenn die Nachbarschaft kleiner wird und sich 0 nähert, mit Ausnahme des Regressionspunktes. Bei sehr kleinen Nachbarschaften entspricht die effektive Anzahl der Koeffizienten der Anzahl der Beobachtungen. Lokale Koeffizientenschätzungen weisen eine große Varianz, jedoch nur eine geringe Verzerrung auf. Die effektive Anzahl wird verwendet, um zahlreiche andere Diagnosemessungen zu berechnen.
- Angepasster kritischer Wert von Pseudo-T-Statistiken: Dies ist der angepasste kritische Wert, mit dem die statistische Signifikanz der Koeffizienten in einem zweiseitigen T-Test mit einer Konfidenz von 95 Prozent getestet werden. Der Wert entspricht einem Signifikanzniveau (Alpha) von 0,05 geteilt durch die effektiven Freiheitsgrade. Diese Anpassung steuert den FWER-Wert der Signifikanz der erklärenden Variablen.
Ausgabediagramme
Eine Scatterplotmatrix sowie Boxplots und ein Histogramm der abweichenden Residuen werden bereitgestellt.
Anzahl (Poisson)
Beim Poisson-Modelltyp wird davon ausgegangen, dass die Werte der abhängigen Variable Anzahlwerte sind.
Feature-Class und hinzugefügte Felder
Die Ausgabe-Features enthalten Felder für den Schnittpunkt (INTERCEPT), den Standardfehler des Schnittpunktes (SE_INTERCEPT), die Koeffizienten und die Standardfehler jeder erklärenden Variablen sowie den vorhergesagten Wert vor der logarithmischen Transformation (RAW_PRED), den vorhergesagten Wert, das abweichende Residuum, GInfluence, die lokale prozentuale Abweichung und den Bedingungswert.
Interpretieren von Meldungen und Diagnosen
Die Meldungen enthalten Analysedetails, einschließlich der Anzahl der analysierten Features, der abhängigen und erklärenden Variablen und der Anzahl der angegebenen Nachbarn. Darüber hinaus werden die folgenden Diagnosen gemeldet:
- % Abweichung, die durch das globale Modell (nicht räumlich) erklärt wird: Dies ist ein Maß für die Anpassungsgüte, das die Performance eines globalen Modells (GLR) quantifiziert. Der Wert variiert von 0.0 bis 1.0, wobei höhere Werte vorzuziehen sind. Er kann als Anteil der abhängigen Variablenvarianz durch das Regressionsmodell interpretiert werden.
- % Abweichung, die durch das lokale Modell erklärt wird: Dies ist ein Maß für die Anpassungsgüte, das die Performance des lokalen Modells (GWR) quantifiziert. Der Wert variiert von 0.0 bis 1.0, wobei höhere Werte vorzuziehen sind. Er kann als Anteil der abhängigen Variablenvarianz durch das lokale Regressionsmodell interpretiert werden.
- % Abweichung, die durch das lokale im Vergleich zum globalen Modell erklärt wird: Dieser Anteil ist eine Möglichkeit, die Vorteile des Umstiegs von einem globalen Modell (GLR) auf ein lokales Regressionsmodell (GWR) zu beurteilen, indem die Restsumme von Quadraten des lokalen Modells mit der Restsumme von Quadraten des globalen Modells verglichen wird. Der Wert variiert von 0,0 bis 1,0, wobei höhere Werte angeben, dass das lokale Regressionsmodell besser abgeschnitten hat als ein globales Modell.
- AICc: Hierbei handelt es sich um einen Messwert für die Modell-Performance, der verwendet werden kann, um Regressionsmodelle zu vergleichen. Unter Berücksichtigung der Modellkomplexität bietet das Modell mit dem niedrigeren AICc-Wert eine bessere Übereinstimmung mit den beobachteten Daten. AICc ist kein absolutes Maß für die Anpassungsgüte, ist aber hilfreich für das Vergleichen von Modellen mit unterschiedlichen erklärenden Variablen, solange sie die gleiche abhängige Variable betreffen. Wenn sich die AICc-Werte für zwei Modelle um mehr als 3 unterscheiden, wird das Modell mit dem niedrigeren AICc-Wert als besser betrachtet. Das Vergleichen des AICc-Werts aus GWR mit dem AICc-Wert aus OLS ist eine Möglichkeit, um die Vorteile des Umsteigens von einem globalen Modell (OLS) auf ein lokales Regressionsmodell (GWR) zu beurteilen.
- Sigma-Squared: Dieser Wert ist die normalisierte Residuenquadratsumme, wobei die Residuenquadratsumme durch die effektiven Freiheitsgrade des Residuums dividiert wird. Dies ist die Least-Squares-Schätzung der Varianz (Quadrat der Standardabweichung) für die Residuen. Kleinere Werte dieser Statistik sind vorzuziehen. Sigma-Squared wird für AICc-Berechnungen verwendet.
- Sigma-Squared – MLE: Dies ist die Maximum-Likelihood-Schätzung (Maximum Likelihood Estimate, MLE) der Varianz (Quadrat der Standardabweichung) für die Residuen. Kleinere Werte dieser Statistik sind vorzuziehen. Zur Berechnung dieses Wertes wird die Restsumme von Quadraten durch die Anzahl der Eingabe-Features dividiert.
- Effektive Freiheitsgrade: Dieser Wert spiegelt einen Kompromiss zwischen der Varianz der angepassten Werte und der Verzerrung in den Koeffizientenschätzungen wider und steht im Zusammenhang mit der ausgewählten Nachbarschaftsgröße. Da sich die Nachbarschaft der Unendlichkeit nähert, nähern sich die geographischen Gewichtungen für jedes Feature dem Wert 1, und die Koeffizientenschätzungen liegen sehr nah an den Schätzungen für ein globales GLR-Modell. Bei sehr großen Nachbarschaften nähert sich die effektive Anzahl von Koeffizienten der tatsächlichen Anzahl. Lokale Koeffizientenschätzungen weisen eine kleine Varianz auf, sind aber verzerrt. Umgekehrt nähern sich die geographischen Gewichtungen für jedes Feature dem Wert 0, wenn die Nachbarschaft kleiner wird und sich 0 nähert, mit Ausnahme des Regressionspunktes. Bei sehr kleinen Nachbarschaften entspricht die effektive Anzahl der Koeffizienten der Anzahl der Beobachtungen. Lokale Koeffizientenschätzungen weisen eine große Varianz, jedoch nur eine geringe Verzerrung auf. Die effektive Anzahl wird verwendet, um zahlreiche andere Diagnosemessungen zu berechnen.
- Angepasster kritischer Wert von Pseudo-T-Statistiken: Dies ist der angepasste kritische Wert, mit dem die statistische Signifikanz der Koeffizienten in einem zweiseitigen T-Test mit einer Konfidenz von 95 Prozent getestet werden. Der Wert entspricht einem Signifikanzniveau (Alpha) von 0,05 geteilt durch die effektiven Freiheitsgrade. Diese Anpassung steuert den FWER-Wert der Signifikanz der erklärenden Variablen.
Ausgabediagramme
Der Bereich Inhalt enthält eine Scatterplotmatrix (mit bis zu 19 Variablen) sowie ein Histogramm des abweichenden Residuums und der Normalverteilungslinie.
Weitere Hinweise und Tipps zur Implementierung
In globalen Regressionsmodellen wie GLR sind die Ergebnisse unzuverlässig, wenn zwei oder mehr Variablen Multikollinearität aufweisen (also wenn zwei oder mehr Variablen redundant sind oder das Gleiche aussagen). Das Werkzeug Geographisch gewichtete Regression erstellt eine lokale Regressionsgleichung für jedes Feature im Dataset. Wenn die Werte für eine bestimmte erklärende Variable zur räumlichen Cluster-Bildung neigen, treten wahrscheinlich Probleme mit lokaler Multikollinearität auf. Der Bedingungswert in den Ausgabe-Features gibt an, wann Ergebnisse aufgrund von lokaler Multikollinearität instabil sind. Bleiben Sie skeptisch bei Ergebnissen, in denen die Features einen Bedingungswert größer 30, gleich NULL oder, im Fall von Shapefiles, gleich -1.7976931348623158e+308 haben. Der Bedingungswert ist an den Maßstab angepasst, um die Anzahl der erklärenden Variablen im Modell zu korrigieren. Dies ermöglicht einen direkten Vergleich des Bedingungswertes zwischen Modellen mit einer unterschiedlichen Anzahl von erklärenden Variablen.
Modellentwurfsfehler weisen oft auf globale oder lokale Multikollinearität hin. Um die Problemursache zu ermitteln, führen Sie das Werkzeug Generalisierte lineare Regression aus, und untersuchen Sie den VIF-Wert für jede erklärende Variable. Wenn einige der VIF-Werte sehr groß sind (z. B. größer als 7,5), verhindert die globale Multikollinearität die Berechnung mit dem Werkzeug. Jedoch ist wahrscheinlich eher eine lokale Multikollinearität das Hauptproblem. Versuchen Sie, eine thematische Karte für jede erklärende Variable zu erstellen. Wenn die Karte räumliche Cluster-Bildung von identischen Werten erkennen lässt, entfernen Sie diese Variablen aus dem Modell oder kombinieren Sie diese Variablen mit anderen erklärenden Variablen, um die Wertvariation zu erhöhen. Wenn Sie beispielsweise Immobilienwerte modellieren und für Schlafzimmer wie auch Badezimmer über Variablen verfügen, ist es möglicherweise sinnvoll, diese zu kombinieren, um die Wertvariation zu erhöhen oder sie als kombinierte Größe darzustellen. Vermeiden Sie beim Erstellen von GWR-Modellen die Verwendung von künstlichen oder binären Variablen für räumliche Ordnungen mit Gauß- oder Poisson-Modelltypen, von Kategorievariablen bzw. nominalen Variablen für räumliche Cluster-Bildung mit logistischen Modelltypen oder von Variablen mit wenigen möglichen Werten.
Zudem können Probleme mit lokaler Multikollinearität verhindern, dass das Werkzeug das optimale Entfernungsband bzw. die optimale Anzahl der Nachbarn berechnet. Geben Sie manuelle Intervalle, ein benutzerdefiniertes Entfernungsband oder eine bestimmte Anzahl von Nachbarn an. Untersuchen Sie anschließend die Bedingungswerte in den Ausgabe-Features, um zu ermitteln, bei welchen Features Probleme aufgrund von lokaler Multikollinearität vorliegen (Bedingungswerte größer als 30). Sie können diese Features beim Ermitteln einer optimalen Entfernung bzw. einer optimalen Anzahl an Nachbarn vorübergehend entfernen. Beachten Sie, dass Ergebnisse, die mit Bedingungswerten von größer als 30 verknüpft sind, nicht zuverlässig sind.
Zusätzliche Quellen
Es gibt zahlreiche Ressourcen, in denen Sie mehr über die GLR und GWR erfahren können. Beginnen Sie mit Grundlagen zur Regressionsanalyse, oder arbeiten Sie das Lernprogramm zur Regressionsanalyse durch.
Folgende Ressourcen sind ebenfalls hilfreich:
Brunsdon, C., Fotheringham, A. S., & Charlton, M. E. (1996). "Geographically weighted regression: a method for exploring spatial nonstationarity". Geographical Analysis, 28(4), 281-298.
Fotheringham, Stewart A., Chris Brunsdon, and Martin Charlton. Geographically Weighted Regression: The analysis of spatially varying relationships. John Wiley & Sons, 2002.
Gollini, I., Lu, B., Charlton, M., Brunsdon, C., & Harris, P. (2015). "GWmodel: An R Package For Exploring Spatial Heterogeneity Using Geographically Weighted Models." Journal of Statistical Software, 63(17), 1–50.https://doi.org/10.18637/jss.v063.i17.
Mitchell, Andy. The ESRI Guide to GIS Analysis, Volume 2. ESRI Press, 2005.
Nakaya, T., Fotheringham, A. S., Brunsdon, C., & Charlton, M. (2005). "Geographically weighted Poisson regression for disease association mapping". Statistics in medicine, 24(17), 2695-2717.
Páez, A., Farber, S., & Wheeler, D. (2011). "A simulation-based study of geographically weighted regression as a method for investigating spatially varying relationships". Environment and Planning A, 43(12), 2992-3010.