Funktionsweise von "Oberflächenperzentil (Multiscale)"

Mit der Spatial Analyst-Lizenz verfügbar.

Das Analysieren von Topografie und anderen Oberflächen ist ein wichtiger Bestandteil der vielen Fachgebiete, von Hydrologie bis hin zur Ökologie. Die Ergebnisse dieser Analysen hängen häufig von der räumlichen Auflösung der Daten oder Berechnungen für eine bestimmte topografische Eigenschaft ab. Diese Abhängigkeit hat zu einer Zunahme an Konzepten für die Analyse mit mehreren Maßstäben geführt. Das sind Analysen, bei denen die Berechnungen für mehrere räumliche Auflösungen durchgeführt werden. Diese Konzepte mit mehreren Maßstäben können verwendet werden, um den optimalen Maßstab für die Beschreibung einer Topografie zu ermitteln und zu messen, wie Parameter auf Änderungen des Maßstabs reagieren.

Das Werkzeug Oberflächenperzentil (Multiscale) berechnet das extremste Perzentil bei verschiedenen räumlichen Maßstäben (Nachbarschaften in verschiedenen Größen). Das am weitesten von 50 entfernte Perzentil (z. B. Werte, die näher an 0 oder 100 liegen) wird als extremster Wert für eine bestimmte Zelle erachtet. Die Ausgaben dieses Werkzeugs identifizieren dieses Perzentil für eine Zelle und den Maßstab, in dem es ermittelt wurde.

Die Ausgaben können zum Interpretieren von Features in einem Eingabe-Oberflächen-Raster und ihren zugehörigen Maßstäben verwendet werden. In dem folgenden Beispiel sind die Ergebnisse von zwei verschiedenen Maßstäben für dieselbe Oberfläche dargestellt. In der ersten Abbildung (links) wurde ein Maßstab von 29 x 29 Zellen verwendet, während in der zweiten Abbildung (rechts) ein Maßstab von 49 x 49 Zellen verwendet wurde. Dabei ist der kleinere Maßstab sensibler hinsichtlich der lokalen Variation in der Landschaft und er erfasst kleinere Oberflächen-Features. Dagegen werden bei einem größeren Maßstab weniger Details angezeigt, indem nur größere Oberflächen-Features erfasst werden.

Die Perzentil-Ausgabe in derselben Ausdehnung wird für zwei verschiedene Maßstäbe angezeigt: einen kleinen Maßstab (zweite Grafik) und einen größeren Maßstab (dritte Grafik).

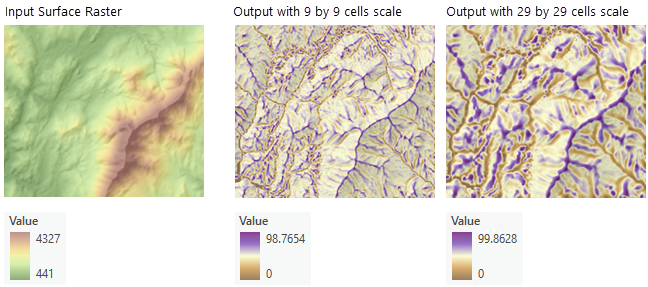
Berechnung des extremsten Perzentilwertes

Die folgenden Schritte geben einen Überblick über die von dem Werkzeug verwendeten internen Prozesse:

1. Die Maßstäbe für die Analyse werden durch die Parameter Minimale Nachbarschaftsentfernung, Maximale Nachbarschaftsentfernung, Basisentfernungsschrittgröße und Nichtlinearitätsfaktor definiert. Die Einheiten dieser Parameter werden durch den Parameter Entfernungseinheiten gesteuert.
2. Für jede Zelle wird das Perzentil in jedem ermittelten Maßstab berechnet.
3. Die berechneten Perzentile bei verschiedenen Maßstäben werden verglichen. Das am weitesten von 50 entfernte Perzentil wird als extremstes Perzentil für eine bestimmte Zelle erachtet.

Jeder dieser Schritte wird in den folgenden Abschnitten ausführlicher erläutert.

Identifizierung der zu analysierenden Maßstäbe

Die Maßstäbe für die Analyse werden unter Verwendung der optionalen Parameter im Werkzeug Oberflächenperzentil (Multiscale) festgelegt. Die Parameter Minimale Nachbarschaftsentfernung und Maximale Nachbarschaftsentfernung legen die minimalen und maximalen Maßstäbe für die Analyse fest. Die Parameter Basisentfernungsschrittgröße und Nichtlinearitätsfaktor steuern die Zunahme der Nachbarschaftsentfernung zwischen dem Minimum und dem Maximum.

Jeder Maßstab wird in Form seiner Nachbarschaftsentfernungswerte dargestellt. Die Analyse wird abhängig von den festgelegten Eingabeparametern für mehrere Nachbarschaftsentfernungen durchgeführt.

Für eine bestimmte Zielzelle wird die Nachbarschaftsentfernung von dem Mittelpunkt der Zielzelle nach außen gemessen, wobei ein Quadrat aus Zellen um die Zielzelle erstellt wird. Zum Beispiel führt eine Nachbarschaftsentfernung von 30 Metern für ein Eingabe-Oberflächen-Raster mit einer Zellengröße von 10 Metern zu einer Nachbarschaft von 7 x 7 Zellen, wie in der folgenden Abbildung zu sehen ist. Dieser Wert von 30 Metern wäre einer der Maßstäbe, für den das extremste Perzentil berechnet wird.

Gezeigt wird die Beziehung zwischen der Nachbarschaftsentfernung (orangefarbene Linie) und der Pixel-Anzahl des bewegten Fensters. Bei einer Zellengröße von 10 Metern verwendet eine Nachbarschaftsentfernung von 10 Metern ein Zellenfenster der Größe 3 x 3 (Standardeinstellung), eine Nachbarschaftsentfernung von 20 Metern ein Zellenfenster der Größe 5 x 5 und eine Nachbarschaftsentfernung von 30 Metern ein Zellenfenster der Größe 7 x 7.

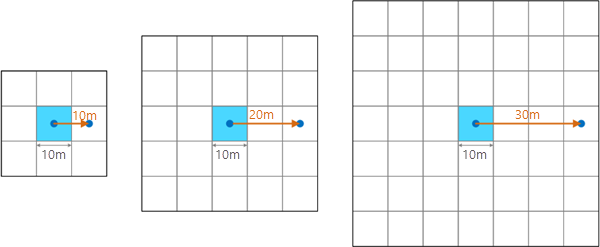
Die geringste zulässige Nachbarschaftsentfernung entspricht der Zellengröße des Eingabe-Rasters. Dies ist der Wert einer Zelle und erzeugt eine 3x3-Zellennachbarschaft. Im obigen Beispiel beträgt diese minimale Nachbarschaftsentfernung 5 Meter.

Die Nachbarschaftsentfernung darf nicht größer sein als das Eingabe-Oberflächen-Raster.

Wenn eine Nachbarschaftsentfernung angegeben wird, die nicht zu einem Intervall der Zellengröße führt, rundet das Werkzeug die Entfernung auf das nächste Intervall der Zellengröße auf. Wenn in der Abbildung weiter oben eine Nachbarschaftsentfernung von 25 Metern angegeben wurde, wird sie auf das nächste Intervall der Zellengröße, also auf 30 Meter aufgerundet.

Die Berechnungen beginnen mit dem Parameterwert Minimale Nachbarschaftsentfernung, und danach wird jede folgende Nachbarschaftsentfernung berechnet.

Der Ausdruck für die Berechnung der folgenden zu verwendenden Nachbarschaftsentfernungen lautet wie folgt:

ni = no + [Δn × (i - no)]p

• Wobei gilt:

  n_i = Nachbarschaftsentfernung für Schritt i

  n_o = Minimale Nachbarschaftsentfernung

  Δn = Basisentfernungsschrittgröße

  i = Der Schritt, für den die Nachbarschaftsentfernung berechnet wird (wobei der erste Schritt einen Wert von 1+n_o hat)

  p = Nichtlinearitätsfaktor

Jede neu ermittelte Nachbarschaftsentfernung wird geprüft, um zu bestimmen, ob sie kleiner oder gleich dem Parameterwert Maximale Nachbarschaftsentfernung ist. Wenn der neue Entfernungswert kleiner oder gleich dem Maximum ist, werden die Berechnungen der Nachbarschaftsentfernung fortgesetzt. Ist der neue Wert größer als das Maximum, so sind alle Nachbarschaftsentfernungen ermittelt worden und die Perzentilberechnungen beginnen.

Weitere Informationen zu diesem Bereich der Analyse finden Sie unten in dem Abschnitt Berechnung des Perzentils.

Auswirkung des Nichtlinearitätsfaktors auf die Nachbarschaftsentfernungen

Der Parameter Nichtlinearitätsfaktor steuert das Raster der Erhöhung der Nachbarschaftsentfernung. Der Standardwert ist 1. Dies führt zu einer linearen Erhöhung der Nachbarschaftsentfernung. Das bedeutet, dass die Inkremente zwischen den Nachbarschaftsentfernungen dem Parameterwert Basisentfernungsschrittgröße entsprechen.

Bei einer Erhöhung des Parameterwerts Nichtlinearitätsfaktor über 1 ändern sich die Inkremente zwischen den Nachbarschaftsentfernungen nach dem ersten Inkrement. Das erste Inkrement entspricht dem Wert von Basisentfernungsschrittgröße, aber alle folgenden Inkremente werden schrittweise größer.

Wenn der Parameterwert Nichtlinearitätsfaktor auf Werte über 1 festgelegt ist, wird das Inkrement in der Entfernung zwischen aufeinander folgenden Nachbarschaftsentfernungen nach dem ersten Inkrement schrittweise erhöht. Eine weitere Folge ist, dass ein höherer Nichtlinearitätsfaktor für dieselben minimalen und maximalen Nachbarschaftswerte insgesamt zu weniger Nachbarschaftsentfernungen führt.

In der folgenden Abbildung wird der Effekt von drei verschiedenen Einstellungen des Parameters Nichtlinearitätsfaktor dargestellt. In diesem Beispiel sind die Einstellungen 1,0, 1,5 und 2,0. Für jede dieser Einstellungen werden die Werte der anderen Parameter beibehalten. Der Parameterwert Minimale Nachbarschaftsentfernung ist 1, der Wert für Maximale Nachbarschaftsentfernung ist 10 und der Wert für Basisentfernungsschrittgröße ist 1.

Für das erste Inkrement ist der Wert für die Nachbarschaftsentfernung für alle drei Einstellungen des Nichtlinearitätsfaktors gleich, also 2 Zellen. Danach ändern sich die Werte für die Nachbarschaftsentfernung. Die Inkremente werden für einen Nichtlinearitätsfaktor von 1,5 schrittweise größer, und das noch mehr bei einem Faktor von 2,0.

Ist der Parameterwert für Nichtlinearitätsfaktor 1,0, so gibt es insgesamt 9 Inkremente, und jedes Inkrement ist linear größer als das vorige. Bei einem Wert von 1,5 für den Faktor gibt es nur 4 Inkremente, bei einem Wert von 2,0 3 Inkremente.

Die Erhöhung des Nichtlinearitätsfaktors über 1 führt zur schrittweisen Erhöhung der Größen des Inkrements, und dadurch wird die Nachbarschaftsentfernung schneller größer. Das führt auch dazu, dass weniger Maßstäbe für dieselbe minimale Nachbarschaftsentfernung und maximale Nachbarschaftsentfernung vorhanden sind, wenn ein größerer Wert für den Nichtlinearitätsfaktor verwendet wird.

Mit dem Parameter Nichtlinearitätsfaktor können Sie die Dichte der Referenzpunkterfassung von Maßstäben anpassen. Bei der Höhenoberfläche ist das Höhenperzentil oft hinsichtlich der Nachbarschaftsgröße bei kleineren Maßstäben empfindlicher und bei größeren Maßstäben weniger empfindlich. Durch die Verwendung eines Parameterwerts größer als 1,0 für den Nichtlinearitätsfaktor kann die Dichte der Maßstabsreferenzpunkterfassung bei kleineren Maßstäben höher und bei größeren Maßstäben geringer sein. Gegebenenfalls müssen Sie jedoch den Parameterwert Maximale Nachbarschaftsentfernung in diesen Fällen erhöhen, um die gewünschte Anzahl Inkremente zu erhalten. In den meisten Fällen wird für den Nichtlinearitätsfaktor ein Wert zwischen 1,0 und 2,0 verwendet.

Berechnung des Perzentils

Perzentile sind ein statistischer Messwert, der den Prozentsatz der Werte in einem Dataset angibt, die unter einen bestimmten Wert fallen. Das 80. Perzentil ⁱst zum Beispiel der Wert, bei dem 80 % der Werte in dem Dataset niedriger und die verbleibenden 20 % der Werte höher sind.

Für jede zur Berechnung ermittelte Nachbarschaftsentfernung und jede Zelle im Eingabe-Oberflächen-Raster berechnet das Werkzeug Oberflächenperzentil (Multiscale) das Perzentil. Die extremsten Perzentilwerte werden im Parameterwert Ausgabe-Perzentil-Raster ermittelt und erfasst. Die Maßstäbe, bei denen diese Perzentile ermittelt wurden, werden als Zellenwerte im Parameterwert Ausgabe-Maßstabs-Raster erfasst.

Die Gleichung für die Berechnung von Perzentilen für jede Zelle lautet wie folgt:

Perzentil = counti ∈C(zi < z0) × (100/nC)

• Wobei gilt:

  C = Die für die Verarbeitung ermittelte Nachbarschaft

  count_{i ∈C} = Die Anzahl der Zellen in Nachbarschaft C, in denen gilt, dass (z_i<z₀) "true" ist

  z_i = Der Wert der Zelle i in Nachbarschaft C

  z₀ = Der Wert der mittleren Zelle von Nachbarschaft C

  n_C = Die Anzahl der in Nachbarschaft C enthaltenen Zellen

Ein Beispiel dieser Berechnung wird im Folgenden mit einer Nachbarschaft von 3x3 Zellen dargestellt.

Der Maßstab ist 3 x 3 Zellen, sie hat insgesamt 9 Zellen. Auf der linken Seite werden der Wert der Verarbeitungszelle und die 8 umgebenden Zellenwerte (grau) identifiziert. Auf der rechten Seite werden die Zellen angezeigt, deren Wert geringer als die mittlere Zelle ist (grün) sowie Werte, die gleich der mittleren Zelle oder größer sind (hellbraun).

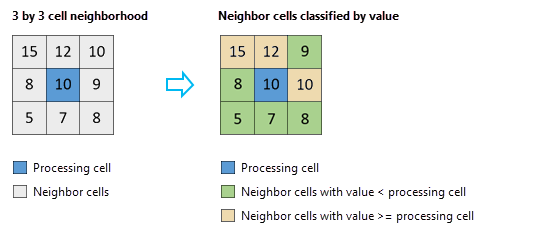
Die Anwendung der oben genannten Formel auf dieses Beispiel führt zu folgendem Ergebnis:

Perzentil = (Anzahl der Zellenwerte, die geringer sind als der Wert der mittleren Zelle)* 100 / (Anzahl der Zellen in der Nachbarschaft) = 5 * 100 / 9 = 55.5556

Dieser Ansatz verwendet den Filteralgorithmus von Huang et al. (1979) für das laufende Histogramm, um die Perzentilwerte nach Bedarf zu gruppieren. Sobald ein Perzentilwert gefunden wurde, wird der Wert mit dem zuvor identifizierten extremsten Perzentil verglichen. Ist der neue Wert extremer, ist also ein Perzentil weiter von 50 entfernt, so wird der Wert für diese Position im Parameterwert Ausgabe-Perzentil-Raster erfasst. Der Maßstabswert wird im Parameterwert Ausgabe-Maßstabs-Raster erfasst.

Verwendung einer GPU

Mit diesem Werkzeug kann die Performance gesteigert werden, wenn Sie eine bestimmte GPU-Hardware auf Ihrem System installiert haben. Weitere Informationen zur Unterstützung, Konfiguration und Aktivierung dieser Funktion finden Sie unter GPU-Verarbeitung mit Spatial Analyst.

Referenzen

Huang, Thomas S., G. Yang und G. Tang. 1979. "A fast two-dimensional median filtering algorithm." IEEE Transactions on Acoustics, Speech, and Signal Processing Band 27, Ausgabe 1. S. 13–18. https://doi.org/10.1109/TASSP.1979.1163188

Newman, Daniel R., John B. Lindsay und Jaclyn Mary Helen Cockburn. 2018. "Evaluating metrics of local topographic position for multiscale geomorphometric analysis." Geomorphology 312, 40–50. https://doi.org/10.1016/j.geomorph.2018.04.003