Funktionsweise von "Bivariate räumliche Zuordnung (Lee's L)"

Das Werkzeug Bivariate räumliche Zuordnung (Lee's L) misst die räumliche Zuordnung (Abhängigkeit) zwischen zwei kontinuierlichen Variablen anhand der Berechnung der Lee's L-Statistik. Die Statistik charakterisiert den Korrelationsgrad der Variablen und deren Copatterning (die Ähnlichkeit des räumlichen Clustering). Die Lee's L-Statistik liegt zwischen -1 und 1 und ähnelt konzeptionell einem Korrelationskoeffizienten, wird aber angepasst, um die räumliche Autokorrelation der beiden Variablen zu berücksichtigen. Lee's L-Werte nahe 1 deuten darauf hin, dass die Variablen in hohem Maße positiv korreliert sind (wenn ein Wert hoch ist, ist der andere tendenziell auch hoch) und dass jede Variable eine hohe räumliche Autokorrelation aufweist (hohe und niedrige Werte der Variablen neigen jeweils zur Cluster-Bildung). Werte nahe -1 deuten darauf hin, dass die Variablen in hohem Maße negativ korreliert sind (wenn ein Wert hoch ist, ist der andere tendenziell niedrig) und dass jede Variable eine hohe räumliche Autokorrelation aufweist. Werte nahe 0 deuten darauf hin an, dass die Variablen nicht räumlich zugeordnet sind, was bedeutet, dass sie entweder nicht korreliert oder nicht räumlich autokorreliert sind. Die Statistik kann auch lokal auf jedes Eingabe-Feature partitioniert und kategorisiert werden, sodass Sie untersuchen können, wie sich die räumliche Zuordnung der Analysevariablen in einem Untersuchungsgebiet ändert.

Die Berücksichtigung der räumlichen Autokorrelation der Variablen ist für die Bewertung der räumlichen Zuordnung zwischen den Analysevariablen von wesentlicher Bedeutung, da herkömmliche statistische Tests auf der Grundlage der Pearson-Korrelation nicht gültig sind, wenn die Variablen räumlich autokorreliert sind. Darüber hinaus bewerten diese herkömmlichen Tests nicht das Copatterning der beiden Variablen, obwohl dies einen wesentlichen Aspekt der räumlichen Beziehung zwischen den Variablen darstellt.

Die Lee's L-Statistik wird berechnet, indem die Korrelation der lokalen Nachbarschaftsdurchschnitte der beiden Analysevariablen kombiniert und die Korrelation durch räumliche Glättungsskalare jeder Analysevariablen angepasst wird. Die räumlichen Glättungsskalare sind Werte zwischen 0 und 1. Glättungsskalare nahe 1 deuten auf eine starke räumliche Autokorrelation (positiv oder negativ) hin, und Werte nahe 0 deuten darauf hin, dass die Werte räumlich zufällig und nicht autokorreliert sind. Niedrige räumliche Glättungsskalare verringern die Lee's L-Statistik im Vergleich zur Pearson-Korrelation, um das fehlende räumliche Clustering der Variablen zu berücksichtigen.

Die folgenden Abbildungen zeigen verschiedene Beispiele für Karten von zwei Analysevariablen und die zugehörigen Pearson-Korrelationen und Lee's L-Statistiken für die Variablen. In jedem Bild haben die blauen Dreiecke den Wert 1 und die orangefarbenen Dreiecke den Wert 0.

In der ersten Abbildung unten haben beide Analysevariablen an jedem Ort die gleichen Werte, sodass ihre Pearson-Korrelation gleich 1 ist. Darüber hinaus weisen sie jeweils eine hohe positive räumliche Autokorrelation auf, wobei hohe und niedrige Werte einen Cluster bilden. Daraus ergibt sich eine Lee's L-Statistik von 0,801, was auf eine hohe positive räumliche Zuordnung zwischen den Variablen hinweist.

In der zweiten Abbildung unten werden die Werte der zweiten Analysevariablen um ein Dreieck nach rechts verschoben, sodass 30 der 54 Dreiecke übereinstimmende Werte aufweisen. Daraus ergibt sich eine Pearson-Korrelation von 0,167. Aufgrund der starken räumlichen Autokorrelation der einzelnen Analysevariablen ist die Lee's L-Statistik jedoch etwas höher: 0,186. Dies deutet auf eine schwache bis mäßige positive räumliche Zuordnung zwischen den Variablen hin.

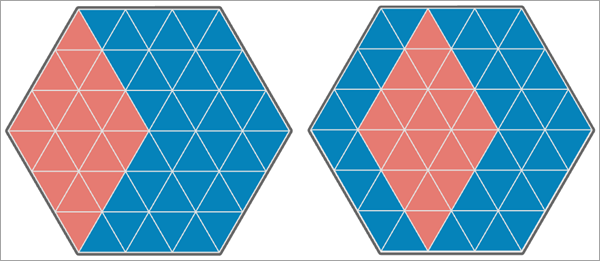
In der dritten Abbildung unten wurden die Werte der zweiten Analysevariablen auf die andere Seite des sechseckigen Untersuchungsgebiets verschoben, und 18 der 54 Dreiecke haben übereinstimmende Werte. Daraus ergibt sich eine Pearson-Korrelation von -0,500, und die Lee's L-Statistik beträgt -0,490, was auf eine mittlere bis starke negative räumliche Zuordnung zwischen den Variablen hinweist.

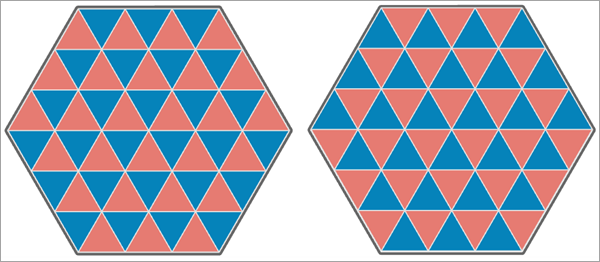
In der letzten Abbildung unten weisen beide Analysevariablen eine negative räumliche Autokorrelation auf, und keines der Dreiecke hat denselben Wert. Daraus ergibt sich eine Pearson-Korrelation von -1, und die Lee's L-Statistik beträgt -0,204, was auf eine schwache bis mittlere negative räumliche Zuordnung zwischen den Variablen hinweist.

Lee's L-Statistik

Die Lee's L-Statistik kann auf jedes Eingabe-Feature partitioniert werden, um zu sehen, wie sich die räumliche Zuordnung zwischen den Variablen räumlich und lokal verändert. Einige Regionen oder Orte können aufgrund wechselnder lokaler Korrelationen und lokaler räumlicher Glättung eine höhere oder niedrigere räumliche Zuordnung aufweisen als die gesamte (globale) Lee's L-Statistik. Sie können feststellen, ob die lokale räumliche Zuordnung höher oder niedriger ist als die globale räumliche Zuordnung, indem Sie die Werte der lokalen Lee's-L-Statistiken direkt mit der globalen Lee's-L-Statistik vergleichen. Im Gegensatz zur globalen Statistik können die lokalen Statistiken größer als 1 oder kleiner als -1 sein, und der Durchschnitt der lokalen Statistiken ist immer gleich der globalen Statistik.

Sie können die lokalen Lee's L-Statistiken auch in verschiedene Kategorien einteilen, die auf ihrer statistischen Signifikanz und den Werten der Nachbarschaften jedes Features basieren. Für jedes Feature gibt es fünf mögliche Kategorien: Not Significant, High-High, High-Low, Low-High und Low-Low. Wenn die lokale Lee's L-Statistik für ein Feature nicht zu mindestens 90% signifikant ist, wird es als nicht signifikant eingestuft. Andernfalls, wenn der Nachbarschaftsdurchschnitt der ersten Analysevariablen größer ist als der Durchschnitt der ersten Analysevariablen und der Nachbarschaftsdurchschnitt der zweiten Variablen größer ist als der Durchschnitt der zweiten Variablen, wird sie als High-High klassifiziert. Wenn die erste Variable kleiner als der Durchschnitt ist und die zweite Variable größer als der Durchschnitt, wird sie als Low-High (und umgekehrt) eingestuft. Es ist wichtig, zwischen diesen Kategorien zu unterscheiden, denn wenn die beiden Variablen positiv räumlich zugeordnet sind, bedeutet dies, dass niedrige Werte der beiden Variablen zur Cluster-Bildung neigen, und ebenso die hohen Werte dazu tendieren, Cluster zu bilden. Beide Situationen führen jedoch zu großen lokalen Lee's L-Statistiken, sodass die Kategorien klären, ob jedes Feature eine hohe Zuordnung aufweist, weil beide Variablen hoch sind oder weil beide Variablen niedrig sind. In ähnlicher Weise klären die Klassifizierungen bei negativer räumlicher Zuordnung, ob ein Feature eine negative lokale Lee's L-Statistik aufweist, weil die erste Variable hoch und die zweite Variable niedrig ist, oder ob die erste Variable niedrig und die zweite Variable hoch ist.

Bei der Ausführung in einer aktiven Karte wird der Ausgabe-Feature-Layer auf der Grundlage dieser fünf Kategorien gezeichnet. Bei räumlich positiv zugeordneten Variablen (globale Lee's L-Statistik größer als 0) enthält der Layer hauptsächlich Kategorien vom Typ High-High und Low-Low. Bei räumlich negativ zugeordneten Variablen (globale Lee's L-Statistik kleiner als 0) enthält der Layer hauptsächlich Kategorien vom Typ High-Low und Low-High.

Beispielanwendungsfälle

Das Werkzeug kann in den folgenden Szenarien verwendet werden:

• Untersuchung der räumlichen Zuordnung zwischen Bildungsstand und Haushaltseinkommen in verschiedenen Stadtteilen einer Großstadt. Entsprechen Gebiete mit höherer Bildung auch Gebieten mit höherem Haushaltseinkommen?
• Erforschung der räumlichen Zuordnung zwischen Vegetationsdecke und Luftqualität. Haben Gebiete mit mehr Vegetation tendenziell eine bessere Luftqualität? Ist die Zuordnung statistisch signifikant?
• Gibt es einen Zusammenhang zwischen Kriminalitätsraten und Immobilienwerten? Ändert sich das Verhältnis in den verschiedenen Regionen eines Ballungsgebietes?

Permutationen und p-Werte

Sie können die globalen und lokalen Lee's L-Statistiken mithilfe von Permutationen auf statistische Signifikanz testen. Bei den Permutationen werden alle Werte der beiden Analysevariablen nach dem Zufallsprinzip einem neuen Ort zugewiesen (wobei die beiden Werte an jedem neuen Ort gepaart bleiben), und die globalen und lokalen Lee's-L-Statistiken werden für die permutierten Werte berechnet. Dieser Prozess wird viele Male wiederholt (gesteuert durch den Wert des Parameters Anzahl der Permutationen), wodurch Referenzverteilungen entstehen, die mit den ursprünglichen globalen und lokalen Lee's L-Statistiken verglichen werden können. Wenn der ursprüngliche Wert nahe der Extremwerte (rechts oder links) der Referenzverteilung liegt, bedeutet dies, dass der ursprüngliche Wert wahrscheinlich nicht das Ergebnis einer zufälligen Variation ist und die räumliche Zuordnung statistisch signifikant ist. Der p-Wert für die globale Lee's L-Statistik wird als Geoverarbeitungsmeldung zurückgegeben, und die p-Werte und Signifikanzniveaus der lokalen Lee's L-Statistiken werden als Felder der Ausgabe-Feature-Class zurückgegeben. Weitere Informationen finden Sie im nachfolgenden Abschnitt Ausgaben des Werkzeugs.

Hinweis:

Die p-Werte werden berechnet, indem die Anzahl der permutierten Werte, die extremer sind als der ursprüngliche Wert, gezählt, um eins erhöht und durch die Anzahl der Permutationen plus eins geteilt wird. Diese Anpassung des Zählers und des Nenners wird vorgenommen, um kleine Stichproben zu berücksichtigen und um sicherzustellen, dass die p-Werte niemals gleich null sind. Der Wert wird dann verdoppelt, sodass der p-Wert aus einem beidseitigen Hypothesentest stammt. Die Seite des Tests wird durch die Seite bestimmt, die einen geringeren Anteil an höheren Extremwerten aufweist (permutierte Werte, die größer oder kleiner als der ursprüngliche Wert sind). Die p-Werte der lokalen Lee's L-Statistiken sind nicht für den multiplen Hypothesentest bereinigt, was bei der Interpretation eines bestimmten lokalen p-Wertes zu berücksichtigen ist.

Nachbarschaftstypen

Die globalen und lokalen Lee's L-Statistiken erfordern eine Nachbarschaft um jedes Feature, um die räumliche Zuordnung zu schätzen. Sie können die Nachbarschaft jedes Features mit dem Parameter Nachbarschaftstyp festlegen. Der Parameter verfügt über die unten beschriebenen Optionen zur Definition der Features, die als Nachbarn für jedes einzelne Feature verwendet werden. Bei allen Nachbarschaftstypen wird das Feature in seine eigene Nachbarschaft aufgenommen.

• Festes Entfernungsband: Alle Features innerhalb einer angegebenen Entfernung werden als Nachbar verwendet (maximal 1.000 Features). Die Standardentfernung ist die kürzeste Entfernung, bei der jedes Feature mindestens einen zusätzlichen Nachbarn hat. Geben Sie die Entfernung über den Parameter Entfernungsband an. Bei Polygonen wird zur Bestimmung der Nachbarn die Entfernung zwischen Schwerpunkten verwendet.

  

• Nächste Nachbarn (K): Eine feste Anzahl von Features, die dem fokalen Feature am nächsten sind, werden als Nachbarn verwendet. Geben Sie den Wert über den Parameter Anzahl der Nachbarn an. Dieser Wert enthält das Feature selbst nicht. Die in der Berechnung verwendete Anzahl von Features ist um Eins größer als der angegebene Wert. Bei Polygonen wird zur Bestimmung der Nachbarn die Entfernung zwischen Schwerpunkten verwendet.

  

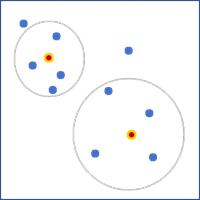
• Nur benachbarte Kanten: Polygone, die eine Kante mit dem Feature gemeinsam haben, werden als Nachbarn verwendet. Diese Option kann nur für Polygon-Features verwendet werden.

  

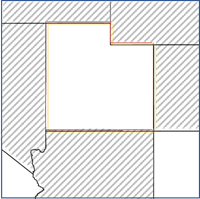
• Benachbarte Kanten/Ecken: Polygone, die eine Kante oder eine Ecke mit dem Feature gemeinsam haben, werden als Nachbarn verwendet. Diese Option kann nur für Polygon-Features verwendet werden.

  

• Delaunay-Triangulation: Nachbarn werden dadurch definiert, dass sie gemeinsame Kanten oder Ecken in ihrer Delaunay-Triangulation (Thiessen-Polygone) haben, die auf die konvexe Hülle der Punkte zugeschnitten werden. Diese Option kann nur für Punkt-Features verwendet werden.

  

• Räumliche Gewichtungen aus Datei abrufen: Die Nachbarn und Gewichtungen alle Features werden durch eine im Parameter Gewichtungsmatrix-Datei angegebene Datei mit räumlicher Gewichtungsmatrix definiert. Sie können die Datei mithilfe eines der beiden folgenden Werkzeuge erstellen: Räumliche Gewichtungsmatrix erstellen oder Räumliche Gewichtung des Netzwerks generieren.

Bei Entfernungsband und Anzahl der Nachbarn können Nachbarn, die näher am Feature liegen, mit einer Kernel-Funktion, die mit der Entfernung abnimmt, höher gewichtet werden. Um nähere Nachbarn stärker zu gewichten, geben Sie die Option Biquadrat für den Parameter Lokales Gewichtungsschema an.

Der Biquadrat-Kernel definiert Gewichtungen mithilfe der folgenden Formel:

Die Kernel-Funktion ist abhängig von einer Bandbreite, mit der gesteuert wird, wie schnell sich die Gewichtungen mit zunehmender Entfernung verringern. Die Bandbreite für jede Kernel-Funktion wird im Parameter Kernel-Bandbreite bereitgestellt. Wenn Sie für die Nachbarschaft "Nächste Nachbarn (K)" keinen Bandbreitenwert angeben, wird für jedes Feature eine andere (adaptive) Bandbreite verwendet, die der Entfernung zum Nachbarn (k+1) des Features entspricht. Beim Nachbarschaftstyp "Entfernungsband" entspricht der Standardwert der Kernel-Bandbreite dem Wert des Parameters Entfernungsband.

Hinweis:

Alle Features haben eine Gewichtung von 1 für die Gewichtung des Features selbst, auch wenn die Datei mit den räumlichen Gewichtungen diese Gewichtungen nicht zugewiesen hat. Zusätzlich werden die Gewichtungen für die Nachbarschaft jedes Features so normalisiert, dass die Summe 1 ergibt (sogenannte Reihen-Standardisierung).

Werkzeugausgaben

Das Werkzeug erzeugt eine Vielzahl von Ausgaben, mit denen Sie die räumliche Zuordnung zwischen den beiden Analysevariablen untersuchen können. Die Ergebnisse werden als eine Geoverarbeitungsmeldung, eine Ausgabe-Feature-Class und ein Scatterplotdiagramm zurückgegeben.

Geoverarbeitungsmeldungen

Die vom Werkzeug zurückgegebenen Geoverarbeitungsmeldungen enthalten Werte, die sich auf die gesamte räumliche Zuordnung zwischen den beiden Analysevariablen beziehen. Die folgenden Werte werden in den Meldungen angezeigt:

• Globale Lee's L-Statistik: Die Lee's L-Statistik zwischen zwei Analysewerten. Der Wert liegt zwischen -1 und 1. Positive Werte weisen auf eine positive räumliche Zuordnung hin, während negative Werte auf eine negative räumliche Zuordnung hinweisen. Werte nahe 0 weisen darauf hin, dass die Variablen nicht räumlich zugeordnet sind. Die Statistik ist eine Kombination aus der Korrelation der Nachbarschaftsdurchschnittswerte zwischen den Analysevariablen und dem Grad der räumlichen Autokorrelation der einzelnen Analysevariablen.
• Globaler p-Wert: Der globale p-Wert eines beidseitigen Tests für eine statistisch signifikante räumliche Zuordnung. Niedrige p-Werte deuten darauf hin, dass die globale Lee's L-Statistik statistisch signifikant ist und nicht auf zufällige Variationen zurückzuführen ist. Wenn der p-Wert signifikant ist (unter 0,1 für eine 90-prozentige Signifikanz, unter 0,05 für eine 95-prozentige Signifikanz und unter 0,01 für eine 99-prozentige Signifikanz) und die globale Lee's L-Statistik positiv ist, sind die beiden Analysevariablen signifikant positiv räumlich zugeordnet. Wenn der p-Wert signifikant und die globale Lee's L-Statistik negativ ist, sind die Analysevariablen signifikant negativ räumlich zugeordnet.
• Skalarwert für räumliches Glätten (Analysefeld 1): Ein Wert zwischen 0 und 1, der den Grad der räumlichen Autokorrelation der ersten Analysevariablen angibt. Werte nahe 1 deuten auf eine starke positive räumliche Autokorrelation hin (hohe und niedrige Werte neigen zur Clusterbildung), und Werte nahe 0 deuten auf eine starke negative räumliche Autokorrelation hin (hohe Werte neigen dazu, von niedrigen Werten umgeben zu sein und umgekehrt).
• Skalarwert für räumliches Glätten (Analysefeld 2): Ein Wert zwischen 0 und 1, der den Grad der räumlichen Autokorrelation der zweiten Analysevariablen angibt.
• Pearson-Korrelation (unverarbeitet): Pearson-Korrelation zwischen den beiden Analysevariablen. Dieser Wert ist nützlich für einen Vergleich mit der globalen Lee's L-Statistik, um den Unterschied zwischen der unverarbeiteten Korrelation der Variablen und ihrer räumlichen Zuordnung zu erkennen.
• Pearson-Korrelation (Nachbarschaftsdurchschnitte): Pearson-Korrelation zwischen den gewichteten Nachbarschaftsdurchschnittswerten der beiden Analysevariablen. Die globale Lee's L-Statistik ist ebenfalls ungefähr gleich diesem Wert, multipliziert mit den Quadratwurzeln der Skalarwerte für das räumliche Glätten.

Die globale Lee's L-Statistik, der globale p-Wert und die Pearson-Korrelation (unverarbeitet) werden ebenfalls als abgeleitete Ausgaben des Werkzeugs zurückgegeben.

Feature-Class und Felder

Die Ausgabe-Feature-Class enthält die folgenden Felder, in denen die Ergebnisse der lokalen Lee's L-Statistik zusammengefasst sind:

• Kopien der beiden Analysevariablen und ein Feld der Quell-ID für jedes Eingabe-Feature.
• Lokale räumliche Zuordnung (LOCAL_L): Die lokale Lee's L-Statistik für jedes Feature. Werte größer als 0 weisen auf eine positive räumliche Zuordnung zwischen den Analysevariablen an der Position hin, Werte kleiner als 0 auf eine negative räumliche Zuordnung.
• Gewichteter Nachbarschaftsdurchschnitt von (erster Analysevariable) (NWA_VAR1): Der gewichtete Nachbarschaftsdurchschnitt der ersten Analysevariablen für jedes Feature. Der Wert ist der gewichtete Durchschnitt der Werte des Features und seiner Nachbarn unter Verwendung der durch die Parameter Nachbarschaftstyp, Lokales Gewichtungsschema und Kernel-Bandbreite definierten Gewichtungen.
• Gewichteter Nachbarschaftsdurchschnitt von (zweiter Analysevariable) (NWA_VAR2): Der gewichtete Nachbarschaftsdurchschnitt der zweiten Analysevariablen für jedes Feature.
• p-Wert (P_VALUE): Der p-Wert für einen beidseitigen Hypothesentest auf statistische Signifikanz der lokalen Lee's L-Statistik für jedes Feature.
• Signifikanzniveau (SIG_LEVEL): Das höchste erreichte Signifikanzniveau der lokalen Lee's L-Statistik für jedes Feature. Mögliche Werte sind "Nicht Signifikant", "90% signifikant", "95% signifikant" und "99% signifikant".
• Kategorie der lokalen räumlichen Zuordnung (ASSOC_CAT): Die Kategorie der lokalen räumlichen Zuordnung für jedes Feature. Mögliche Werte: Not Significant, High-High, High-Low, Low-High und Low-Low. Low-High bedeutet beispielsweise, dass das Feature zu mindestens 90% signifikant ist. Der gewichtete Nachbarschaftsdurchschnitt der ersten Analysevariablen ist kleiner als der Durchschnitt der ersten Analysevariablen, und der gewichtete Nachbarschaftsdurchschnitt der zweiten Analysevariablen ist größer als der Durchschnitt der zweiten Analysevariablen.
• Anzahl der Nachbarn (NUM_NBRS): Die Anzahl der Nachbarn (einschließlich des Features), die zur Berechnung der globalen und lokalen Lee's L-Statistik für jedes Feature verwendet wurden.

Lee's L-Scatterplot

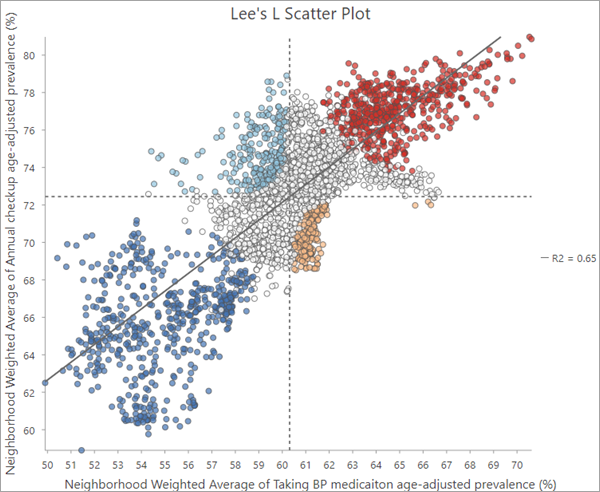
Der Ausgabe-Feature-Layer enthält ein Lee's L-Scatterplotdiagramm, das die gewichteten Nachbarschaftsdurchschnittswerte der ersten Analysevariablen auf der x-Achse und die gewichteten Nachbarschaftsdurchschnittswerte der zweiten Analysevariablen auf der y-Achse zusammen mit einer an die Daten angepassten linearen Trendlinie anzeigt. Außerdem sind gestrichelte horizontale und vertikale Linien an den Mittelwerten der einzelnen Analysevariablen eingezeichnet. Diese Linien unterteilen den Scatterplot in vier Quadranten und dienen der Einteilung der Punkte in die Kategorien der lokalen räumlichen Zuordnung. Statistisch signifikante Features im oberen linken Quadranten werden zum Beispiel der Kategorie Low-High (hellblau) zugeordnet.

Das Diagramm kann auch verwendet werden, um einzelne Features zu identifizieren, die von den allgemeinen Trends der übrigen Features abweichen. Sie können zum Beispiel einzelne Punkte im Scatterplot auswählen, die weit von der Trendlinie entfernt liegen, um diese Features weiter zu untersuchen. Möglicherweise stellen Sie fest, dass sich diese Features in der Karte bündeln und regionale Muster in der räumlichen Zuordnung erkennen lassen, die sonst nur schwer zu erkennen sind.

Empfehlungen und Beschränkungen

Berücksichtigen Sie bei Verwendung dieses Werkzeugs Folgendes:

• Ausreißer (Werte, die viel größer oder kleiner sind als der Rest der Werte) in einer der beiden Analysevariablen beeinflussen die Ergebnisse erheblich. Es wird empfohlen, Histogramme für jede Analysevariable zu erstellen, um festzustellen, ob Ausreißer vorhanden sind, und um alle Features zu entfernen, die Ausreißer in einer der Variablen enthalten. Sie können auch Data Engineering zur Identifizierung von Ausreißern verwenden.
• Bei der Verwendung dieses Werkzeugs wird davon ausgegangen, dass eine lineare Beziehung zwischen den gewichteten Nachbarschaftsdurchschnittswerten der beiden Analysevariablen besteht. Wenn die Werte im Lee's L-Scatterplotdiagramm ein nicht lineares Muster aufweisen, können Sie das Werkzeug Feld transformieren verwenden, um Transformationen auf die Analysevariablen anzuwenden, mit denen die Beziehung zwischen ihnen linear wird, und das Werkzeug mit den transformierten Werten erneut ausführen.
• Ein statistisch signifikanter p-Wert (in der Regel kleiner als 0,05) bedeutet nicht unbedingt, dass eine Kreuzkorrelation zwischen den beiden Variablen besteht. Es könnte stattdessen nur bedeuten, dass eine oder beide Variablen eine hohe räumliche Autokorrelation aufweisen. Um einen signifikanten p-Wert zu interpretieren, überprüfen Sie die Werte der globalen Lee's L-Statistik, die Korrelation zwischen den Nachbarschaftsdurchschnittswerten und den Skalarwert der räumlichen Glättung jeder Variablen. Anhand dieser Werte können Sie die Quelle der statistischen Signifikanz interpretieren: Autokorrelation, Kreuzkorrelation oder beides. Wenn der p-Wert signifikant ist, aber die globale Lee's L-Statistik und die Korrelation zwischen den Nachbarschaftsdurchschnittswerten sehr nahe bei 0 liegen und die Skalarwerte der räumlichen Glättung nahe bei 1 liegen, bedeutet dies wahrscheinlich, dass die Variablen jeweils stark autokorreliert sind, aber nur eine geringe Kreuzkorrelation zwischen ihnen besteht.
• Es wird empfohlen, mindestens 50 Eingabe-Features zu verwenden und für jedes Feature mindestens 8 Nachbarn einzubeziehen.

Formeln

Dieser Abschnitt enthält die Formeln für alle Statistiken, die mit dem Werkzeug berechnet werden. Ableitungen und weitere Informationen finden Sie in den Abhandlungen im Abschnitt "Referenzen" unten.

In allen Formeln steht x für die erste Analysevariable und y für die zweite Analysevariable. Eine Tilde (~) über einer Variablen zeigt an, dass es sich um einen gewichteten Durchschnitt der Nachbarschaftswerte handelt. Die Gewichtungen für jede Nachbarschaft werden normalisiert, so dass sie sich zu 1 summieren. Ein Balken über einer Variablen zeigt an, dass es sich um einen ungewichteten Durchschnitt aller n Eingabe-Features handelt. Das tiefgestellte i steht für ein einzelnes Feature. Alle Summen in den Formeln addieren sich über alle Eingabe-Features.

Die globale Lee's L-Statistik wird mit der folgenden Formel berechnet:

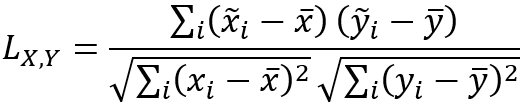
Die globale Lee's L-Statistik ist auch annähernd gleich dem Produkt aus den Quadratwurzeln der Skalarwerte der räumlichen Glättung und der Korrelation zwischen den gewichteten Nachbarschaftsdurchschnittswerten wie nachfolgend dargestellt:

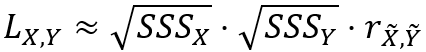
Die Skalarwerte für die räumliche Glättung werden mit den folgenden Formeln berechnet:

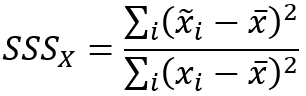
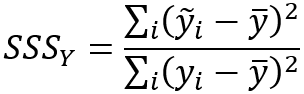
Die Korrelation zwischen den gewichteten Nachbarschaftsdurchschnittswerten wird mit der folgenden Formel berechnet:

Die lokale Lee's L-Statistik wird mit der folgenden Formel berechnet:

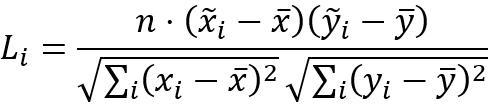
Die globale Lee's L-Statistik ist gleich dem Durchschnitt der lokalen Lee's L-Statistiken wie nachfolgend dargestellt:

Referenzen

Bei der Implementierung des Werkzeugs wurden folgende Ressourcen verwendet:

• Lee, Sang-Il. "Developing a bivariate spatial association measure: an integration of Pearson's r and Moran's I." Journal of geographical systems 3 (2001): 369–385. https://doi.org/10.1007/s101090100064.
• Lee, Sang-Il. "A generalized randomization approach to local measures of spatial association." Geographical Analysis 41.2 (2009): 221–248. https://doi.org/10.1111/j.1538-4632.2009.00749.x.