Funktionsweise von "Analyse der kausalen Inferenz"

Mit dem Werkzeug Analyse der kausalen Inferenz wird der kausale Effekt zwischen einer kontinuierlichen Expositionsvariable und einer kontinuierlichen Ergebnisvariable geschätzt, indem konfundierende Variablen ausgeglichen werden. Das Werkzeug weist durch den Wahrscheinlichkeits-Score-Abgleich oder die Umkehrung von Wahrscheinlichkeits-Score-Gewichtungen einzelnen Beobachtungen Gewichtungen zu, sodass die Korrelation der konfundierenden Variablen mit der Expositionsvariable aufgehoben und der kausale Effekt zwischen Exposition und Ergebnis isoliert wird. Das Ergebnis ist eine Exposure-Response-Funktion (ERF), mit der geschätzt wird, wie die Ergebnisvariable auf Änderungen der Expositionsvariable reagiert. So können Sie beispielsweise die durchschnittliche Steigerung des Maisertrags (Ergebnis) bei verschiedenen Düngermengen (Exposition) schätzen und konfundierende Variablen wie Bodenart, Bewirtschaftungsmethoden und Umgebungsvariablen, die sich ebenfalls auf die Maisproduktion auswirken, dabei außen vor lassen. Die ERF wird als Scatterplot und als Bild in den Geoverarbeitungsmeldungen angezeigt. Darüber hinaus können Sie den kausalen Effekt einzelner Beobachtungen abschätzen und zweckgebundene Ziele erstellen. Sie können beispielsweise schätzen, welche Düngermenge eine Farm benötigt, um eine bestimmte Maismenge im Jahr zu erzeugen.

Hintergrund der Analyse der kausalen Inferenz

Die Analyse der kausalen Inferenz zählt zu einem Statistikfeld, das Ursache-Wirkungs-Beziehungen zwischen zwei untersuchten Variablen modelliert. Eine Variable (die sogenannte Expositions- oder Verfahrensvariable) hat eine direkte Änderung einer anderen Variable (als Ergebnisvariable bezeichnet) zur Folge bzw. wirkt sich direkt auf diese aus. Korrelationen gelten oft als Maß dafür, wie Änderungen bei einer Variable mit Änderungen an der anderen Variable zusammenhängen. Eine Korrelation bedeutet jedoch nicht zwingend, dass eine Variable eine ursächliche Wirkung auf eine andere Variable hat. Es wäre auch möglich, dass beide Variablen dem Einfluss anderer Faktoren unterliegen. So kann die Beziehung zwischen dem Verkauf von Eis und dem Verkauf von Sonnenschutzcreme auf ein starkes positives Verhältnis zwischen den beiden hindeuten. Es wäre jedoch falsch, deshalb zu dem Schluss zu kommen, dass höhere Verkaufszahlen bei Eis zu höheren Verkaufszahlen bei Sonnenschutzcreme führen. Andere Faktoren wie Temperatur, UV-Index oder Kalendermonat müssen ebenfalls in die Überlegungen einbezogen werden, bevor kausale Schlüsse gezogen werden können. Die Faktoren, die sich gleichermaßen auf die Expositions- und Ergebnisvariable auswirken, werden als konfundierende Variablen bezeichnet. Es ist sehr wichtig, diese zu berücksichtigen, um die Ursache-Wirkungs-Beziehung zwischen der Expositions- und Ergebnisvariable richtig zu erfassen.

Am Anfang einer kausalen Analyse steht eine Hypothese, die sich auf Recherchen oder das Allgemeinwissen stützt. Ein Beispiel dafür wäre die Bedeutung von Bewegung für die Gesundheit. Es ist erwiesen und Bestandteil des Allgemeinwissens, dass sich regelmäßige Bewegung positiv auf die Gesundheit auswirkt. Die Variablen sind jedoch auch von zahlreichen anderen konfundierenden Variablen abhängig, z. B. Essensgewohnheiten, Lebensstil und Zugang zu einer sicheren Trainingsumgebung. In solchen Fällen kann die Analyse der kausalen Inferenz verwendet werden, um den Effekt der Expositionsvariable (z. B. die tägliche Trainingszeit) auf die Ergebnisvariable (z. B. gesundheitliche Folgen) zu isolieren, nachdem verschiedene wichtige konfundierende Variablen berücksichtigt wurden.

In Versuchsplänen werden konfundierende Variablen mit randomisiert kontrollierten Studien (Randomized Controlled Trials; RCTs) gesteuert. RCTs sind in der klinischen Forschung weit verbreitet. Dabei werden den Teilnehmern nach dem Zufallsprinzip unterschiedliche Expositionsstufen zugewiesen, und die Ergebnisse werden miteinander verglichen. Beispielsweise trainiert eine Person 10 Minuten am Tag, eine andere eine Stunde und eine dritte überhaupt nicht. Da die Expositionsvariablen nach dem Zufallsprinzip zugewiesen wurden, können Unterschiede bei den Gesundheitsdaten ausschließlich auf die Expositionsvariablen zurückgeführt werden.

In der Realität ist es jedoch oft unmöglich oder unethisch, kontrollierte Experimente durchzuführen. Um die Auswirkungen der Luftverschmutzung auf Despressionen zu untersuchen, wäre es beispielsweise aus ethischen Gründen nicht möglich, Menschen einer hohen Luftverschmutzung auszusetzen, um herauszufinden, wie sich dies auf ihre Depressionen auswirkt. Stattdessen können Sie nur den Verschmutzungsgrad, dem die Menschen bereits ausgesetzt sind, und die Stärke ihrer Depression beobachten. Mit einer Analyse der kausalen Inferenz lässt sich dann die kausale Beziehung der Beobachtungsdaten modellieren, indem ein kontrollierter Versuchsplan imitiert wird. Dazu wird für jede Beobachtung ein Wahrscheinlichkeits-Score geschätzt. Anhand der Wahrscheinlichkeits-Scores wird dann eine Reihe von Ausgleichsgewichtungen für die Beobachtungen angenommen. Bei der Konfiguration der Ausgleichsgewichtungen wird berücksichtigt, dass die kausale Beziehung zwischen der Expositions- und der Ergebnisvariable erhalten bleibt, der Effekt der konfundierenden Variablen auf die Expositionsvariable wird jedoch entfernt. Auf diese Weise wird eine unverfälschte Schätzung der kausalen Beziehung möglich gemacht. Die resultierenden gewichteten Beobachtungen verfügen über Eigenschaften, die einem im Rahmen eines RCT erfassten Datasets entsprechen, und Sie können ebenso Rückschlüsse ziehen wie bei den im Rahmen einer Versuchsplanung erfassten Datasets.

Zwei wichtige Methoden zum Schätzen der Ausgleichsgewichtungen sind der Wahrscheinlichkeits-Score-Abgleich und die Umkehrung der Wahrscheinlichkeits-Score-Gewichtung. Beim Wahrscheinlichkeits-Score-Abgleich wird jede Beobachtung mit verschiedenen anderen Beobachtungen abgeglichen. Diesen Beobachtungen liegen ähnliche konfundierende Variablen (gemessen nach Ähnlichkeit der Wahrscheinlichkeits-Scores) zugrunde, sie verfügen jedoch über unterschiedliche Expositionswerte. Durch den Vergleich des Ergebniswerts einer Beobachtung mit dem Ergebniswert der zugehörigen Gegenstücke können Sie erkennen, wie der Ergebniswert der Beobachtung bei anderen Expositionswerten ausgesehen haben könnte. Die Ausgleichsgewichtung, die den einzelnen Beobachtungen zugewiesen wird, entspricht der Anzahl der Abgleiche mit einer anderen Beobachtung. Bei der Umkehrung der Wahrscheinlichkeits-Score-Gewichtung werden Ausgleichsgewichtungen zugewiesen, indem die Wahrscheinlichkeits-Scores umgekehrt und mit der allgemeinen Wahrscheinlichkeit der Exposition multipliziert werden. Durch diese Vorgehensweise nimmt die Repräsentation ungewöhnlicher Beobachtungen (Beobachtungen mit niedrigem Wahrscheinlichkeits-Score) zu und die Repräsentation häufiger Beobachtungen (mit hohem Wahrscheinlichkeits-Score) ab, sodass der Einfluss der konfundierenden Variablen über den gesamten Wertebereich der Expositionsvariable im richtigen Verhältnis beibehalten wird.

Die Ausgleichsgewichtungen aus dem Wahrscheinlichkeits-Score-Abgleich oder der Umkehrung der Wahrscheinlichkeits-Score-Gewichtung reichen nicht immer aus, um die konfundierenden Variablen hinreichend auszugleichen. Deshalb werden ihre gewichteten Korrelationen mit einem Schwellenwert verglichen. Wenn die Korrelationen unter dem Schwellenwert liegen (und die Korrelation entsprechend schwach ist), lassen sie sich problemlos ausgleichen und eine ERF wird geschätzt. Wenn die Ausgleichsgewichtungen die konfundierenden Variablen jedoch nicht ausreichend ausgleichen, wird vom Werkzeug ein Fehler zurückgegeben und keine ERF erzeugt.

Beispielanwendungen

Im Folgenden werden beispielhaft einige Anwendungsbereiche des Werkzeugs vorgestellt:

• Untersuchung darüber, wie sich Werbung für Tabakprodukte auf den Tabakkonsum von Jugendlichen in den Vereinigten Staaten auswirkt. In diesem Beispiel wäre die Expositionsvariable die Menge an Werbung, denen einzelne Jugendliche ausgesetzt sind, und die Ergebnisvariable die Menge an Tabak, die von diesen Jugendlichen innerhalb eines bestimmten Zeitraums konsumiert wird. Bei den konfundierenden Variablen sollte es sich um alle anderen Variablen handeln, die erwiesenermaßen oder vermutlich mit der Exposition bzw. dem Konsum von Tabakprodukten durch Jugendliche in Zusammenhang stehen, z. B. sozioökonomische Variablen, direkte Exposition gegenüber Tabakprodukten durch Familie oder Freunde sowie der Preis und die Verfügbarkeit von Tabakprodukten. Viele Expositionsvariablen würden sich dazu eignen, den Tabakkonsum von Jugendlichen zu untersuchen (etwa die direkte Exposition gegenüber Tabakprodukten durch Familienmitglieder). Werbung für Tabakprodukte ist jedoch eine nützliche Expositionsvariable, da sie durch gesetzliche Regelungen eingeschränkt werden kann, wenn sich herausstellen sollte, dass sie tatsächlich einen großen Einfluss auf den Tabakkonsum von Jugendlichen hat. Die Einschränkung des Tabakkonsums von erwachsenen Familienmitgliedern wäre dagegen nicht so leicht als öffentlicher Grundsatz umzusetzen.
• Schätzung des kausalen Effekts der Düngermenge auf den Maisertrag in der Präzisionslandwirtschaft, wobei die Bodenart, Bewirtschaftungsmethoden, Umgebungsvariablen und anderen konfundierenden Variablen einzelner landwirtschaftlicher Parzellen nicht mit berücksichtigt werden. Beispiel: Wie viel Mais würde zusätzlich erzeugt werden, wenn die Düngermenge auf allen Farmen um 10 Prozent gesteigert werden würde?
• Schätzung des kausalen Effekts zwischen dem Blutdruck und dem Risiko eines Herzinfarkts, wobei konfundierende Variablen wie Alter, Gewicht, soziodemografische Variablen und der Zugang zu Gesundheitseinrichtungen ausgeschlossen werden.
• Bei Geodaten stellen Entfernungen zu anderen Features oft nützliche Expositionsvariablen dar. Beispielsweise führt die Entfernung von Lebensmittelgeschäften, Grünflächen und Krankenhäusern zu Änderungen bei anderen Variablen: mit zunehmender Entfernung von einem Lebensmittelgeschäft wird die Versorgung mit Lebensmitteln schwieriger, dasselbe gilt für die Entfernung von einem Krankenhaus als Voraussetzung für den Zugang zu medizinischer Versorgung usw. Aus ähnlichen Gründen stellen auch räumliche Variablen und Entfernungen zu anderen Features häufig wichtige konfundierende Variablen dar, selbst wenn es sich bei der Expositions- und Ergebnisvariable selbst nicht um räumliche Variablen handelt.

Für die Analyse der kausalen Inferenz gibt es jedoch einige Einschränkungen und Annahmen, die berücksichtigt werden müssen, damit die Schätzungen der kausalen Effekte unverzerrt und gültig sind. Es gelten unter anderem die folgenden Annahmen und Einschränkungen für die Analyse der kausalen Inferenz:

• Alle wichtigen konfundierenden Variablen müssen enthalten sein. Dies ist eine wichtige Annahme bei der Analyse der kausalen Inferenz und bedeutet, dass die Schätzung des kausalen Effekts verzerrt wird, wenn Variablen, die im Zusammenhang mit der Expositions- und der Ergebnisvariable stehen, nicht als konfundierende Variablen einbezogen werden (eine Mischung aus dem kausalen Effekt und dem konfundierenden Effekt fehlender konfundierender Variablen). Das Werkzeug kann nicht ermitteln, ob alle wichtigen konfundierenden Variablen einbezogen wurden. Daher ist es entscheidend, dass Sie bei der Angabe der konfundierenden Variablen wohlüberlegt vorgehen. Wenn es wichtige konfundierende Variablen gibt, die nicht verfügbar sind, werten Sie die Ergebnisse mit äußerster Vorsicht aus oder verwenden Sie das Werkzeug nicht.
• Die Korrelationen zwischen den konfundierenden Variablen und der Expositionsvariable müssen entfernt werden, um den kausalen Effekt zu isolieren. Bei einer Analyse der kausalen Inferenz wird das Entfernen der Korrelationen zwischen den konfundierenden Variablen und der Expositionsvariable als Ausgleich bezeichnet; das Werkzeug setzt dazu verschiedene Ausgleichsverfahren ein. Die Korrelationen zwischen den konfundierenden Variablen und der Expositionsvariable können jedoch nicht immer hinreichend entfernt werden. Wenn beim Ausgleichsverfahren kein ausreichender Ausgleich der konfundierenden Variablen erfolgt, wird vom Werkzeug ein Fehler zurückgegeben und keine ERF geschätzt. Weitere Informationen zu dem Fehler und dessen Behebung finden Sie unter Tipps zum Erzielen ausgeglichener konfundierender Variablen.
• Die ERF kann nicht außerhalb des Bereichs der Expositionswerte, die der Schätzung zugrunde liegen, extrapolieren. Wenn es sich bei der Expositionsvariable beispielsweise um die durchschnittliche Jahrestemperatur handelt, können Sie die neuen Ergebnisse nicht für Temperaturen schätzen, die über denen in der Stichprobe liegen. Das kann bedeuten, dass Sie zukünftig möglicherweise keine Ergebnisse vorhersagen können, wenn die mittleren Temperaturen dann einen der aktuellen mittleren Temperaturwerte übersteigen. Darüber hinaus werden das oberste und unterste Prozent der Expositionswerte standardmäßig gekürzt (aus der Analyse entfernt), sodass der ERF-Bereich sogar noch enger ist als die Expositionswerte der Beobachtungen im Beispiel.

Werkzeugausgaben

Das Werkzeug erzeugt eine Vielzahl von Ausgaben, mit denen Sie die kausale Beziehung zwischen der Expositions- und der Ergebnisvariable untersuchen können. Die Ergebnisse werden über einen Grafik-Layer, Geoverarbeitungsmeldungen, Ausgabe-Features (oder eine Ausgabetabelle) und eine Ausgabe-ERF-Tabelle zurückgegeben.

Exposure-Response-Funktion

Das primäre Ergebnis des Werkzeugs ist die ERF, mit der geschätzt wird, wie die Ergebnisvariable auf Änderungen der Expositionsvariable reagiert. Mit der ERF wird der neue Bevölkerungsdurchschnitt (der Durchschnittswert aller Bevölkerungsmitglieder) der Ausgabevariable geschätzt, wenn die Expositionsvariable für alle Bevölkerungsmitglieder in denselben Variablenwert geändert wird, alle vorhandenen konfundierenden Variablen jedoch gleich bleiben. Wenn beispielsweise für alle US-Countys als Expositionsvariable PM 2,5 (Feinstaub kleiner als 2,5 Mikrometer) und als Ergebnisvariable die Hospitalisierungsrate aufgrund von Asthma betrachtet wird, schätzt die ERF, wie sich die durchschnittliche nationale Hospitalisierungsrate aufgrund von Asthma ändert, wenn der nationale Grenzwert für PM 2,5 erhöht oder gesenkt wird. Bei dieser Schätzung werden alle anderen Variablen (z. B. soziodemografische Variablen) unverändert wie vor der Änderung bezüglich PM 2,5 beibehalten.

Bei der Ausführung in einer aktiven Karte wird ein Scatterplotdiagramm eingebunden, bei dem die Ausgabe-Features die ERF anzeigen. Zudem wird in den Meldungen ein Bild der ERF angezeigt.

Mit der ERF wird der Durchschnittswert der Ergebnisvariable (Y-Achse) geschätzt, wenn die Expositionsvariable für alle Mitglieder der Grundgesamtheit zum selben Wert geändert wird (X-Achse).

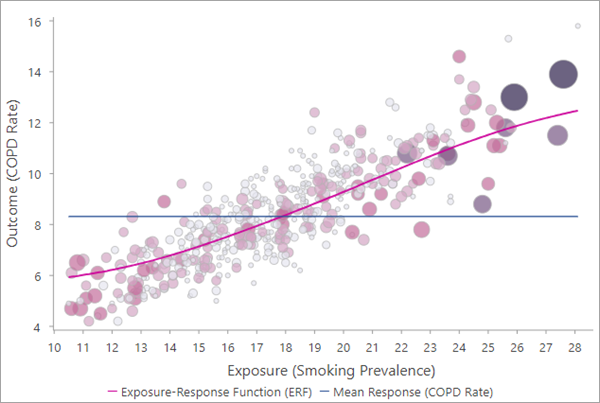
Die rosafarbene Kurve stellt die ERF zwischen der Expositionsvariable (X-Achse) und der Ergebnisvariable (Y-Achse) dar. Die Beobachtungen werden im Scatterplot als Punkte dargestellt, wobei größere Punkte darauf hinweisen, dass die Features über eine größere Ausgleichsgewichtung verfügen und in größerem Maß zur Schätzung der ERF beigetragen haben. Wenn die Beobachtung beim Wahrscheinlichkeits-Score-Abgleich keine Übereinstimmungen aufweist, wird sie als hellgrauer Punkt gezeichnet. Gekürzte Beobachtungen werden im Diagramm nicht dargestellt.

Die ERF enthält außerdem eine blaue horizontale Linie, die den Durchschnittswert der Ergebnisvariable angibt, damit er mit dem geschätzten Durchschnittswert bei verschiedenen Werten der Expositionsvariable verglichen werden kann. Beispiel: Wenn im Bild oben alle Countys eine einheitliche Raucherquote von unter etwa 18 (der Punkt, an dem die Mittellinie die ERF schneidet) festlegten, würde dies zu einer Abnahme der allgemeinen COPD-Rate (Rate der Personen mit chronisch obstruktiver Lungenerkrankung) führen. Gleichermaßen würde eine Raucherquote von über 18 in allen Countys eine Zunahme der allgemeinen COPD-Rate bedeuten.

Sie können auch mit dem Parameter Exposure-Response-Funktion-Ausgabetabelle eine Tabelle der ERF erstellen. Die ggf. erstellte Tabelle enthält 200 gleichmäßig verteilte Expositionswerte zwischen der minimalen und maximalen Exposition zusammen mit dem entsprechenden Antwortwert (Ergebniswert). Wenn Zielexpositions- oder Zielergebniswerte bereitgestellt werden, werden diese ebenfalls zusammen mit dem geschätzten Expositions- oder Antwortwert am Ende der Tabelle angefügt.

Ausgleich konfundierender Variablen in Statistiken

Im Abschnitt Ausgleichsergebnisse der Meldungen werden die ursprünglichen und gewichteten absoluten Korrelationen zwischen den einzelnen konfundierenden Variablen und der Expositionsvariable angezeigt. Auf diese Weise können Sie feststellen, ob die Ausgleichsgewichtungen die ursprüngliche Korrelation zwischen den konfundierenden Variablen und der Expositionsvariable reduziert haben. Wenn durch die Gewichtungen ein effektiver Ausgleich erzielt wurde, sollten die gewichteten Korrelationen geringer als die ursprünglichen Korrelationen sein. Die letzte Zeile in der Meldungstabelle zeigt den Mittel-, Median- oder Maximalwert der absoluten Korrelation, abhängig vom Wert des Parameters Ausgleichstyp.

Im Diagramm der Meldung "Korrelation zwischen Störfaktoren und Exposition" werden dieselben Informationen wie in der Tabelle angezeigt, jedoch in einem vertikalen Liniendiagramm. Die ursprünglichen Korrelationen der einzelnen konfundierenden Variablen sind durch eine rote Linie verbunden, die gewichteten Korrelationen durch eine blaue Linie. Außerdem werden die ursprünglichen und gewichteten aggregierten Korrelationen entsprechend als rote und blaue vertikale Balken dargestellt. Wenn die Gewichtungen die konfundierenden Variablen effektiv ausgleichen, sollten sich die blauen Linien im Allgemeinen links neben den roten Linien befinden. Der Ausgleichsschwellenwert wird als vertikale gestrichelte Linie gezeichnet, sodass Sie sehen können, wie weit die Korrelationen an den Schwellenwert heranreichten. Im Bild unten beispielsweise begannen zwei der konfundierenden Variablen mit relativ großen Korrelationen (über 0,3 bzw. 0,4), die Ausgleichsgewichtungen reduzierten die Korrelationen jedoch auf weniger als 0,1. Die dritte konfundierende Variable begann bereits mit einer niedrigen Korrelation (etwas weniger als 0,1), die Ausgleichsgewichtungen führten aber dennoch zu einer weiteren leichten Reduzierung der Korrelation. Insgesamt wurde die Korrelation im Mittel von nahezu 0,27 auf unter 0,05 gesenkt.

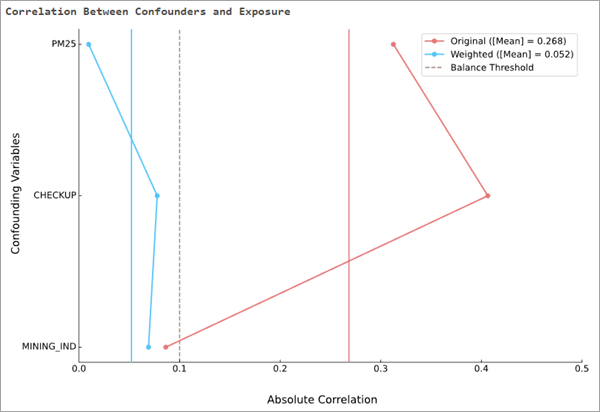
Weitere Informationen zum Ausgleich konfundierender Variablen finden Sie im Abschnitt Überprüfen auf ausgeglichene konfundierende Variablen weiter unten.

Optimierungsergebnisse der Parameter

Die Meldungen enthalten auch Abschnitte mit einer Zusammenfassung der verschiedenen Optimierungsparameter, die zum Schätzen der ERF herangezogen werden. Abhängig von den im Werkzeug angegebenen Parametern können die folgenden Abschnitte angezeigt werden:

• Kürzungsergebnisse: Hier werden die ursprüngliche Anzahl der Beobachtungen (ohne Datensätze mit NULL-Werten), die Anzahl der entfernten Beobachtungen während der Expositionskürzung, die Anzahl der entfernten Beobachtungen während der Kürzung des Wahrscheinlichkeits-Scores und die Anzahl der verbleibenden Beobachtungen nach der Kürzung angezeigt.
• Passende Suchergebnisse im Raster: Beim Wahrscheinlichkeits-Score-Abgleich werden die Ergebnisse der Suche nach passenden Parametern angezeigt. Das Werkzeug verwendet verschiedene Kombinationen der Anzahl der Expositionsabschnitte und der relativen Gewichtung von Wahrscheinlichkeits-Scores zur Exposition (Maßstab) und zeigt die sich ergebenden gewichteten Korrelationen für alle Kombinationen an. Die Kombination, aus der sich die niedrigste gewichtete Korrelation (bester Ausgleich) ergibt, wird fett hervorgehoben.
• Ausgleichsergebnisse der Transformation: Die Transformationen der konfundierenden Variablen, mit denen versucht wurde, einen Ausgleich zu erreichen, werden gemeinsam mit der gewichteten Korrelation für jede Transformationskombination für das Regressionsmodell des Wahrscheinlichkeits-Scores angezeigt. Die Transformationskombination, aus der sich die niedrigste gewichtete Korrelation ergibt, wird fett hervorgehoben.
• Ausgleichsergebnisse der Gradientenverstärkung: Die Ergebnisse der Gradient-Boosting-Rastersuche werden für das Gradient-Boosting-Modell des Wahrscheinlichkeits-Scores angezeigt. Das Werkzeug testet neun Kombinationen der Anzahl von Bäumen und der Lernrate und zeigt die gewichteten Korrelationen für alle Kombinationen an. Die Kombination, aus der sich die niedrigste gewichtete Korrelation ergibt, wird fett hervorgehoben.
• Parameter für besten Ausgleich: Hier werden für den Wahrscheinlichkeits-Score-Abgleich die Anzahl der Expositionsabschnitte und die relative Gewichtung von Wahrscheinlichkeits-Scores zur Exposition (Maßstab) gezeigt, die den besten Ausgleich der konfundierenden Variable ergeben. Bei Gradient Boosting werden die Anzahl der Bäume, die Lernrate und der Ursprungswert des Zufallszahlengenerators gezeigt, die den besten Ausgleich der konfundierenden Variable ergeben.
• Ausgleichsergebnisse: Hier werden die ursprünglichen und gewichteten Korrelationen der einzelnen konfundierenden Variablen sowie der Mittel-, Median- oder Maximalwert der Korrelationen angezeigt. Wenn Transformationen stattgefunden haben, wird auch die Transformation der einzelnen konfundierenden Variablen dargestellt.

Im Abschnitt Schätzen der optimalen Ausgleichsparameter weiter unten finden Sie Informationen dazu, wie viele der Werte in den Meldungen ermittelt werden.

Ausgabe-Features

Die Ausgabe-Features oder -tabelle enthält Kopien der Expositions- und Ergebnisvariable und der konfundierenden Variablen sowie die Wahrscheinlichkeits-Scores, Ausgleichsgewichtungen (Anzahl an Übereinstimmungen oder umgekehrte Wahrscheinlichkeits-Score-Gewichtungen) und ein Feld, in dem angegeben ist, ob der Datensatz gekürzt wurde. Wenn sie einer Karte hinzugefügt werden, werden die Ausgabe-Features basierend auf der Ausgleichsgewichtung dargestellt. Auf diese Weise können Sie feststellen, ob den Gewichtungen räumliche Muster zugrunde liegen, die darauf hinweisen können, dass bestimmte Regionen in den Ergebnissen über- oder unterrepräsentiert sind.

Wenn Sie Zielexpositions- oder Zielergebniswerte angeben, werden von jedem angegebenen Wert zwei zusätzliche Felder in der Ausgabe erstellt. Bei den Zielexpositionswerten enthält das erste Feld den geschätzten Ergebniswert, wenn die Beobachtung die Zielexposition erhalten hat, und das zweite Feld die geschätzte Änderung bei der Ergebnisvariable. Positive Werte deuten darauf hin, dass die Ergebnisvariable sich erhöht, während sie bei negativen Werten sinkt. Bei den Zielergebniswerten enthält das erste Feld den Expositionswert, der zum Zielergebnis führen würde, und das zweite Feld die Änderung, die bei der Expositionsvariable erforderlich ist, um das Zielergebnis zu erreichen.

Wenn Sie Pop-up-Diagramme der lokalen ERF erstellen, wird bei jedem Ausgabedatensatz die lokale ERF im Pop-up-Bereich angezeigt. Alle Zielergebnis- oder Zielexpositionswerte werden als orangefarbene Dreiecke auf der X- und Y-Achse angezeigt. Sie können auf die Dreiecke klicken, um horizontale oder vertikale Balken zu aktivieren und zu deaktivieren und so festzustellen, wo der Wert die lokale ERF schneidet. Darüber hinaus können Sie den Mauszeiger über die Dreiecke bewegen, um Informationen dazu anzuzeigen, welche Änderungen bei der Exposition oder dem Ergebnis erforderlich sind, um das Ziel zu erreichen. Weitere Informationen finden Sie unter Schätzen lokaler kausaler Effekte.

Bei dieser Beobachtung muss die Raucherquote um etwa 1,5 zurückgehen, um den COPD-Zielwert 7 zu erreichen.

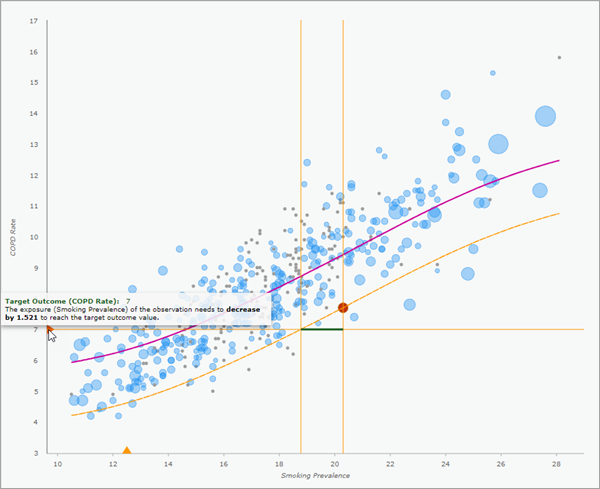
Wenn Sie Bootstrap-Konfidenzintervalle für die ERF erstellen, werden zwei zusätzliche Felder erstellt, in denen angegeben wird, wie oft die Beobachtung in einer Bootstrap-Stichprobe ausgewählt und wie oft die Beobachtung zu einer Bootstrap-Stichprobe, die ausgeglichen werden konnte, hinzugefügt wurde. Es empfiehlt sich, beide Felder im Hinblick auf räumliche Muster zu untersuchen. Wenn einige Regionen sehr viel mehr ausgeglichene Bootstrap-Stichproben als andere Regionen enthalten, sind die Konfidenzintervalle möglicherweise verzerrt. (Das führt normalerweise zu unrealistisch engen Konfidenzintervallen.) Weitere Informationen finden Sie unter Bootstrap-Konfidenzintervalle.

Wahrscheinlichkeits-Scores

Eine grundlegende Komponente der Analyse der kausalen Inferenz ist der Wahrscheinlichkeits-Score. Ein Wahrscheinlichkeits-Score gibt laut Definition die Wahrscheinlichkeit an, mit der eine Beobachtung unter Berücksichtigung der Werte der konfundierenden Variablen den beobachteten Expositionswert annimmt. Ein hoher Wahrscheinlichkeits-Score bedeutet, dass der Expositionswert der Beobachtung bei Personen mit ähnlichen konfundierenden Variablen häufig vorkommt, während ein niedriger Wahrscheinlichkeits-Score bedeutet, dass der Expositionswert bei Personen mit ähnlichen konfundierenden Variablen unüblich ist. Wenn eine Person beispielsweise einen hohen Blutdruck (Expositionsvariable) hat, aber keine Risikofaktoren für hohen Blutdruck (konfundierende Variablen) vorliegen, würde diese Person vermutlich einen niedrigen Wahrscheinlichkeits-Score haben, weil es relativ ungewöhnlich ist, ohne Risikofaktoren einen hohen Blutdruck zu haben. Im Gegensatz dazu würde ein hoher Blutdruck bei einer Person mit vielen Risikofaktoren zu einem höheren Wahrscheinlichkeits-Score führen, da dies häufiger vorkommt.

Zwei Ansätze bezüglich der Analyse der kausalen Inferenz greifen auf den Wahrscheinlichkeits-Score zurück: der Wahrscheinlichkeits-Score-Abgleich und die Umkehrung der Wahrscheinlichkeits-Score-Gewichtung. Bei beiden Ansätzen wird jeder Beobachtung eine Reihe von Ausgleichsgewichtungen zugewiesen, mit denen danach die konfundierenden Variablen ausgeglichen werden. (Weitere Informationen dazu finden Sie unter Überprüfen auf ausgeglichene konfundierende Variablen weiter unten.)

Wahrscheinlichkeits-Score-Abgleich

Beim Wahrscheinlichkeits-Score-Abgleich wird versucht, die konfundierenden Variablen durch den Abgleich der einzelnen Beobachtungen mit verschiedenen Beobachtungen, denen ähnliche konfundierende Variablen, aber verschiedene Expositionswerte zugrunde liegen, auszugleichen. Durch den Vergleich des Ergebniswerts der Beobachtung mit den Ergebnissen der entsprechenden Beobachtungen können Sie erkennen, wie die Ergebnisse der Beobachtung bei einem anderen Expositionswert (und den gleichen konfundierenden Variablen) ausgesehen haben könnten. Nachdem Übereinstimmungen für alle Beobachtungen gefunden wurden, entspricht die Ausgleichsgewichtung, die den einzelnen Beobachtungen zugewiesen wird, der Anzahl der Abgleiche einer Beobachtung mit einer anderen Beobachtung. Wenn eine Beobachtung beispielsweise mit keiner anderen Beobachtung übereinstimmt, ergibt sich als Ausgleichsgewichtung 0, wenn sie dagegen mit allen anderen Beobachtungen übereinstimmt, entspricht die Ausgleichsgewichtung der Anzahl der Beobachtungen.

Der Wahrscheinlichkeits-Score-Abgleich für kontinuierliche Expositionsvariablen ist relativ kompliziert und wird im vierten und fünften Punkt im Abschnitt Referenzen unten vollständig beschrieben und abgeleitet. Sie finden hier eine kurze Zusammenfassung des Abgleichvorgangs:

Der erste Schritt besteht darin, die Beobachtungen anhand des Werts des Parameters Anzahl Expositionsabschnitte basierend auf der Expositionsvariable in gleichmäßige Abschnitte (ähnlich den Abschnitten eines Histogramms) einzuteilen. Der Wahrscheinlichkeits-Score-Abgleich findet innerhalb der einzelnen Abschnitte statt. Dazu werden die Wahrscheinlichkeits-Scores der Beobachtungen im Abschnitt mit den kontrafaktischen Wahrscheinlichkeits-Scores aller anderen Beobachtungen verglichen. Kontrafaktische Wahrscheinlichkeits-Scores sind die Wahrscheinlichkeits-Scores, die eine Beobachtung bei gleichbleibenden konfundierenden Variablen, aber anderen Expositionswerten gehabt hätte (in diesem Fall die mittleren Werte der Expositionsabschnitte). Übereinstimmungen innerhalb der einzelnen Abschnitte werden ermittelt, indem die Beobachtung in dem Expositionsabschnitt gesucht wird, dessen Wahrscheinlichkeits-Score den kontrafaktischen Wahrscheinlichkeits-Scores der einzelnen anderen Beobachtungen am nächsten liegt. Da sich die Expositionswerte der Beobachtungen im Abschnitt jedoch im Allgemeinen nicht mit der Mitte des Abschnitts decken, wird ein zusätzlicher Wert basierend auf der Differenz zwischen dem Expositionswert und dem Wert in der Mitte des Expositionsabschnitts abgezogen. Der Abzugswert ergibt sich aus dem Wert des Parameters Relative Gewichtung von Wahrscheinlichkeits-Score zu Exposition (auch als Maßstabsparameter im Bezug bezeichnet). Die Gesamtübereinstimmung ist die Beobachtung mit der niedrigsten gewichteten Summe der absoluten Differenzen bei den Wahrscheinlichkeits-Scores (Wahrscheinlichkeits-Score minus kontrafaktischer Wahrscheinlichkeits-Score) und der Exposition (ursprüngliche Exposition minus Wert der Abschnittsmitte).

Umkehrung der Wahrscheinlichkeits-Score-Gewichtung

Bei der Umkehrung der Wahrscheinlichkeits-Score-Gewichtung werden jeder Beobachtung Ausgleichsgewichtungen zugewiesen, indem der Wahrscheinlichkeits-Score umgekehrt und mit der allgemeinen Wahrscheinlichkeit des Vorliegens der jeweiligen Exposition multipliziert wird. Bei diesem Ansatz bezüglich der kausalen Inferenz erhalten Beobachtungen mit niedrigen Wahrscheinlichkeits-Scores höhere Ausgleichsgewichtungen und Beobachtungen mit hohen Wahrscheinlichkeits-Scores niedrigere Ausgleichsgewichtungen. Dieses Gewichtungsschema wird damit begründet, dass der Wahrscheinlichkeits-Score ein Maß dafür ist, wie häufig oder selten der Expositionswert für die jeweilige Gruppe konfundierender Variablen ist. Durch die Erhöhung des Einflusses (Erhöhung der Ausgleichsgewichtung) ungewöhnlicher Beobachtungen (Beobachtungen mit niedrigen Wahrscheinlichkeits-Scores) und die Verringerung des Einflusses häufiger Beobachtungen bleiben die Gesamtverteilungen konfundierender Variablen für alle Werte der Expositionsvariable proportional erhalten.

Hinweis:

Die allgemeine Wahrscheinlichkeit für das Vorliegen des Expositionswerts wird mittels Schätzung der Kerndichte (Kernel Density Estimation; KDE) ermittelt. Bei einer KDE wird ein Gauß'scher Kernel mit Silverman-Bandbreite verwendet, wie er in der Funktion scipy.stats.gaussian_kde des SciPy-Python-Pakets implementiert ist.

Schätzung des Wahrscheinlichkeits-Scores

Mithilfe des Parameters Wahrscheinlichkeits-Score-Berechnungsmethode können Sie angeben, wie Wahrscheinlichkeits-Scores geschätzt werden sollen. Bei jeder Methode wird ein Modell erstellt, in dem die konfundierenden Variablen als erklärende Variablen dienen und die Expositionsvariable als abhängige Variable verwendet wird. Es gibt zwei Berechnungsmethoden für den Wahrscheinlichkeits-Score:

• Regression: Für die Schätzung der Wahrscheinlichkeits-Scores wird die Regression "Kleinste Quadrate (Ordinary Least-Squares, OLS)" verwendet.

  Weitere Informationen zur OLS-Regression

• Gradient Boosting: Für die Schätzung der Wahrscheinlichkeits-Scores werden Gradient-Boosting-Regressionsbäume verwendet.

  Weitere Informationen zu Gradient Boosting

Im Regressionsmodell werden den Vorhersagen Wahrscheinlichkeiten zugewiesen, indem normalverteile standardisierte Residuen angenommen werden. In einem Gradient-Boosting-Modell werden nicht automatisch standardisierte Residuen erzeugt, weshalb von dem Werkzeug ein zweites Gradient-Boosting-Modell erstellt wird, um den absoluten Wert der Residuen des ersten Modells vorherzusagen. Dies ergibt eine Schätzung des Standardfehlers. Danach wird eine KDE (wie bei der Umkehrung der Wahrscheinlichkeits-Score-Gewichtung) für die standardisierten Residuen herangezogen, um eine standardisierte Verteilung der Residuen zu erstellen. Mit dieser Verteilung können dann Wahrscheinlichkeits-Scores für alle Wertekombinationen aus Expositionsvariable und konfundierenden Variablen geschätzt werden.

Bei der Regression und Gradient Boosting werden alle Variablen neu skaliert, sodass sie sich zwischen 0 und 1 befinden, bevor die entsprechenden Modelle erstellt werden.

Überprüfen auf ausgeglichene konfundierende Variablen

Damit es sich bei der ERF um eine unverzerrte Schätzung des kausalen Effekts handelt, müssen alle konfundierenden Variablen enthalten und ausgeglichen sein. Das bedeutet, dass konfundierende Variablen keine Korrelation mit der Expositionsvariable aufweisen dürfen. Da konfundierende Variablen definitionsgemäß eine Korrelation mit der Expositionsvariable aufweisen, sind die ursprünglichen konfundierenden Variablen stets nicht ausgeglichen. Der Zweck von Ausgleichsgewichtungen (der Anzahl von Wahrscheinlichkeits-Score-Abgleichen oder der Umkehrung von Wahrscheinlichkeits-Score-Gewichtungen) besteht darin, alle Beobachtungen so zu gewichten, dass die gewichteten Beobachtungen ausgeglichen werden, die kausale Beziehung zwischen der Expositions- und der Ergebnisvariable jedoch unverändert bleibt, sodass eine unverzerrte Schätzung der ERF möglich wird.

Um festzustellen, ob die Ausgleichsgewichtungen die konfundierenden Variablen effektiv ausgleichen, werden gewichtete Korrelationen zwischen den einzelnen konfundierenden Variablen und der Expositionsvariable berechnet. Die absoluten Werte der gewichteten Korrelationen werden anschließend aggregiert und mit einem Schwellenwert verglichen. Wenn die aggregierte Korrelation unter dem Schwellenwert liegt, werden die konfundierenden Variablen als ausgeglichen eingestuft. Sie können den Aggregationstyp (Mittelwert, Medianwert oder Maximum der absoluten Korrelation) angeben, indem Sie den Parameter Ausgleichstyp verwenden und den Schwellenwert im Parameter Ausgleichsschwellenwert angeben. Standardmäßig berechnet das Werkzeug den Mittelwert der absoluten Korrelation und einen Schwellenwert von 0,1.

Hinweis:

Bei kontinuierlichen konfundierenden Variablen werden die gewichteten Korrelationen mithilfe eines gewichteten Korrelationskoeffizienten der Spearman-Rangstufe berechnet. Diese Korrelation ähnelt einem herkömmlichen Pearson-Korrelationskoeffizienten, anstelle der ursprünglichen Werte werden jedoch die gewichteten Rangstufen der Variablen verwendet. Durch die Verwendung von Rangstufen wird die Korrelation robuster gegenüber Ausreißern und ungewöhnlichen Verteilungsmustern. Die Berechnung der gewichteten Korrelationen von kategorialen konfundierenden Variablen erfolgt mithilfe einer gewichteten Eta-Statistik, in der gewichtete Rangstufen der Expositionsvariable verwendet werden. Die Eta-Statistik ist eine nahe Entsprechung der absoluten Pearson-Korrelation für kategoriale Variablen (beide können als Quadratwurzel von R-Squared, dem Bestimmtheitsmaß, definiert werden). Die Verwendung gewichteter Rangstufen anstelle von unverarbeiteten Expositionswerten macht es zu einer nahen Entsprechung des absoluten Wertes einer gewichteten Spearman-Korrelation.

Tipps zum Erzielen ausgeglichener konfundierender Variablen

Wenn die Ausgleichsgewichtungen die konfundierenden Variablen nicht ausreichend ausgleichen, gibt das Werkzeug einen Fehler zurück und erzeugt keine ERF. Es werden aber verschiedene Meldungen mit Informationen zu den gewichteten Korrelationen der einzelnen konfundierenden Variablen angezeigt. Wenn dieser Fehler auftritt, sollten Sie in den Meldungen nachvollziehen, wie stark sich die Korrelationen durch die Ausgleichsgewichtungen reduzierten und wie nah die gewichteten Korrelationen am Ausgleichsschwellenwert lagen.

Wenn vom Werkzeug kein Ausgleich erzielt werden kann, ist zu überlegen, ob relevante konfundierende Variablen fehlen, die es einzubeziehen gilt. Testen Sie als Nächstes verschiedene Optionen der Parameter Wahrscheinlichkeits-Score-Berechnungsmethode und Ausgleichsmethode. Für einige Datasets lässt sich jedoch mit keiner Kombination ein Ausgleich erzielen.

Im Allgemeinen gilt: Je stärker die ursprünglichen Korrelationen zwischen den konfundierenden Variablen sind, desto schwieriger wird es, diese auszugleichen. Bei stark korrelierten konfundierenden Variablen können große Stichprobenmengen erforderlich sein, um einen ausreichenden Ausgleich zu erzielen. Bei kategorialen konfundierenden Variablen wird es mit steigender Kategorienzahl immer schwieriger, einen Ausgleich zu erreichen. Es kann erforderlich sein, einige Kategorien zu kombinieren, vor allem dann, wenn es nur eine geringe Variation der Expositionsvariable gibt oder die einzelnen Kategorien nur wenige Beobachtungen enthalten (im Allgemeinen weniger als fünf).

Wenn es allerdings für Sie akzeptabel ist, dass die ERF eine gewisse Verzerrung aufweist, können Sie den Ausgleich durch die Erhöhung des Ausgleichsschwellenwertes oder die Verwendung eines toleranteren Ausgleichstyps erzielen.

Im Allgemeinen weist ein niedrigerer Ausgleichsschwellenwert auf eine geringere Toleranz für Verzerrungen bei der Schätzung des kausalen Effekts hin. Bei niedrigeren Schwellenwerten ist es jedoch schwieriger, einen Ausgleich zu erzielen. Indem für den Ausgleichstyp der Mittelwert der Korrelationen verwendet wird, ist sichergestellt, dass die konfundierenden Variablen im Durchschnitt ausgeglichen werden. Einige konfundierende Variablen können dennoch große Korrelationen aufweisen, wenn es gleichzeitig genügend andere mit niedrigeren Korrelationen gibt, sodass der Durchschnitt unter dem Schwellenwert liegt. Die Option "Maximum" ist die konservativste Einstellung und erfordert, dass alle konfundierenden Variablen unter dem Schwellenwert liegen. Wenn nur eine einzige Variable geringfügig darüber liegt, werden die konfundierenden Variablen als nicht ausgeglichen betrachtet. Die Option "Medianwert" ist die mildeste Einstellung, bis zu 50 % der Korrelationen können sehr groß sein und gelten dennoch als ausgeglichen.

Schätzen der optimalen Ausgleichsparameter

Es kann sich oft als schwierig erweisen, den Ausgleich konfundierender Variablen zu erreichen, deshalb wird vom Werkzeug versucht, verschiedene Optimierungen und Suchläufe durchzuführen und so Optimierungsparameter zu ermitteln, die zu möglichst ausgeglichenen konfundierenden Parametern führen. Die durchgeführten Optimierungen hängen von verschiedenen Werkzeugparametern ab und werden in den folgenden Abschnitten beschrieben.

Suche nach passenden Parametern

Beim Wahrscheinlichkeits-Score-Abgleich hängen die Ergebnistreffer von den Werten der Parameter Anzahl Expositionsabschnitte und Relative Gewichtung von Wahrscheinlichkeits-Score zu Exposition ab. Es ist jedoch schwierig, die Werte, die zu einem optimalen Ausgleich führen, vorherzusagen. Darüber hinaus können kleine Änderungen eines Wertes zu großen Änderungen bei einem der anderen Werte führen. Deshalb ist es besonders schwierig, ein Wertepaar zu finden, das effektiv eingesetzt werden kann. Wenn keine Werte für die Parameter angegeben wurden, testet das Werkzeug verschiedene Kombinationen und zeigt die Ergebnisse in einer Tabelle in den Meldungen an. In dieser Tabelle entsprechen die Zeilen der Anzahl der Expositionsabschnitte und die Spalten den relativen Gewichtungen (oft als Maßstab bezeichnet). Die gewichtete Korrelation der einzelnen Kombinationen wird im Raster angezeigt, wobei bei jeder Kombination, mit der ein Ausgleich erreicht wurde, ein Sternchen neben dem Wert steht. Die Kombination, aus der sich die niedrigste gewichtete Korrelation (bester Ausgleich) ergibt, wird fett hervorgehoben. Wie im Bild unten gezeigt, können die gewichteten Korrelationen bei verschiedenen Werten für die beiden Parameter beträchtlich schwanken.

Das Werkzeug testet relative Gewichtungen zwischen 0 und 1 in Schritten von 0,2, die Anzahl der getesteten Expositionsabschnitte hängt jedoch von der Anzahl der Beobachtungen ab. Die getesteten Werte liegen im Bereich zwischen der vierten Wurzel und zweimal der Kubikwurzel der Anzahl der Beobachtungen. Die getesteten Werte werden gleichmäßig um mindestens drei inkrementiert, und es werden nicht mehr als 10 Werte getestet.

Regressionstransformationen

Wenn bei der Verwendung der Regression zum Berechnen von Wahrscheinlichkeits-Scores die konfundierenden Variablen nicht ausgeglichen werden, werden verschiedene Transformationen auf alle kontinuierlichen konfundierenden Variablen angewendet. Sobald die konfundierenden Variablen ausgeglichen sind, endet dieser Vorgang, und die ERF wird anhand der aktuellen Reihe von Transformationen erstellt.

Der Vorgang beginnt mit der unausgeglichensten konfundierenden Variable (größte gewichtete Korrelation); es wird eine Reihe von Transformationen angewendet. Die Transformation, mit der der beste Ausgleich erzielt wird, wird beibehalten, und der Vorgang wird für die nächste konfundierende Variable wiederholt. Dies wird fortgesetzt, bis alle konfundierenden Variablen mit allen Transformationen getestet wurden. Wenn die konfundierenden Variablen weiterhin nicht ausgeglichen werden können, wird ein Fehler vom Werkzeug zurückgegeben und keine ERF erzeugt.

Die folgenden Transformationen werden mit Einschränkungen für die Werte der transformierten konfundierenden Variablen durchgeführt:

• Natürlicher Logarithmus: Nur für konfundierende Variablen mit positiven Werten
• Quadrat: Nur für konfundierende Variablen mit nicht negativen Werten
• Quadratwurzel: Nur für konfundierende Variablen mit nicht negativen Werten
• Dritte Potenz
• Kubikwurzel

Die Transformationen, mit denen der beste Ausgleich erzielt wurde, werden im Abschnitt Ausgleichsergebnisse der Meldungen angezeigt. Der vollständige Verlauf der Transformationsversuche wird im Abschnitt Ausgleichsergebnisse der Transformation angezeigt.

Beim Wahrscheinlichkeits-Score-Abgleich werden die Anzahl der Expositionsabschnitte und die Werte der relativen Gewichtung der ursprünglichen (nicht transformierten) konfundierenden Variablen für alle Transformationskombinationen verwendet. Auf diese Weise werden übermäßig lange Berechnungszeiten verhindert, wenn die Suche nach passenden Parametern für jede Transformationskombination wiederholt wird. Die Quadrattransformation ist auf nicht negative Werte beschränkt, sodass sich die Anordnung der Werte der konfundierenden Variablen vor und nach der Transformation nicht ändert. Dies ist wichtig, wenn die Anzahl der Expositionsabschnitte und die relative Gewichtung, die aus den ursprünglichen Beobachtungen bestimmt wird, wiederverwendet werden.

Suche nach Gradient-Boosting-Parametern

Bei Verwendung von Gradient Boosting zum Berechnen der Wahrscheinlichkeits-Scores werden verschiedene Kombinationen der Anzahl von Bäumen und der Lernrate getestet. Sobald die konfundierenden Variablen ausgeglichen sind, endet dieser Vorgang, und die aktuelle Anzahl von Bäumen sowie die Lernrate werden verwendet. In diesem Vorgang werden bis zu neun Kombinationen getestet: Anzahl der Bäume gleich 10, 20 und 30 Bäume und Lernrate gleich 0,1, 0,2 und 0,3.

Die Anzahl der Bäume und die Lernrate, die den besten Ausgleich erzielt, werden im Abschnitt Parameter für besten Ausgleich der Meldungen angezeigt. Der vollständige Verlauf der Parameterkombinationen wird im Abschnitt Ausgleichsergebnisse der Gradientenverstärkung angezeigt.

Im Gegensatz zu den Regressionstransformationen wird die Suche nach passenden Parametern für die Anzahl der Expositionsabschnitte und die relative Gewichtung für jede Kombination aus Anzahl der Bäume und Lernrate wiederholt. Dabei wird eine gründlichere Suche durchgeführt, da kleine Änderungen bei einem dieser vier Parameter zu großen Änderungen bei den optimalen Werten der anderen Parameter führen können.

Schätzen der Exposure-Response-Funktion

Beim Ausgleich werden jeder Beobachtung Ausgleichsgewichtungen (Anzahl an Übereinstimmungen oder Umkehrung der Wahrscheinlichkeits-Score-Gewichtungen) zugewiesen, die als Grundlage für die Schätzung der Exposure-Response-Funktion dienen. Die gewichteten Beobachtungen (manchmal auch als Pseudo-Grundgesamtheit bezeichnet) verfügen über jeweils einen Expositionswert, einen Ergebniswert und eine Gewichtung. Das Ziel besteht darin, eine geglättete Kurve (die ERF) an die gewichteten Beobachtungen anzupassen. Bei der Schätzung der ERF beeinflusst jede Beobachtung die Schätzung proportional zu ihrer Gewichtung. Das bedeutet, eine Beobachtung mit dreifacher Gewichtung trägt so viel wie drei Beobachtungen mit einer einfachen Gewichtung bei. Ebenso hat eine Beobachtung mit der Gewichtung 0 keinen Einfluss auf die ERF, sodass die Beobachtung effektiv ausgefiltert wird.

Für jeden gegebenen Wert der Expositionsvariable (X-Achse) wird der zugeordnete Wirkungswert (Y-Achse) als gewichteter gleitender Durchschnitt (gelegentlich als Kernel-Glätter bezeichnet) der Ergebniswerte der Beobachtungen geschätzt. Die Gewichtungen im gewichteten Durchschnitt entsprechen den Ausgleichsgewichtungen, multipliziert mit der Gewichtung eines Gauß-Kernels und gekürzt an drei Standardabweichungen.

Wenn dieser Vorgang für alle Werte der Expositionsvariable durchgeführt wird, ist das Ergebnis eine geglättete Kurve, die durch die Beobachtungen verläuft und zu den Beobachtungen mit den größten Gewichtungen tendiert.

Bandbreitenschätzung

Der Kernel in der ERF-Formel ist abhängig von einem Bandbreitenwert (der Standardabweichung des Gauß-Kernels), der die Glättung der ERF-Kurve bestimmt. Die Angabe einer entsprechenden Bandbreite ist sehr wichtig für die Erzeugung einer realistischen und genauen ERF. Größere Bandbreitenwerte führen zu glatteren ERFs für dieselbe Reihe an gewichteten Beobachtungen. Im folgenden Bild werden drei Bandbreitenwerte für dieselbe Beobachtung dargestellt:

Mit dem Parameter Methode zur Bandbreitenschätzung können Sie auswählen, wie ein Bandbreitenwert geschätzt werden soll. Es sind drei Methoden zur Bandbreitenschätzung verfügbar:

• Plug-in: Der Bandbreitenwert wird mit einer schnellen Faustregel-Formel geschätzt. Dies ist die Standardoption. Die Berechnung erfolgt schnell und ergibt im Allgemeinen genaue und realistische ERFs. Die Methode ist eine gewichtete Variante der Methodologie von Fan (1996) und leitet den Bandbreitenwert aus der zweiten Ableitung einer gewichteten globalen Polynominterpolation der vierten Ordnung ab, die an alle Beobachtungen angepasst wurde.
• Kreuzvalidierung: Es wird der Bandbreitenwert verwendet, mit dem der Mean Square (MS)-Kreuzvalidierungsfehler minimiert wird. Bei dieser Option dauert die Berechnung am längsten, sie ist jedoch am stärksten in der statistischen Theorie verankert. Bei großen Datasets besteht bei der Kreuzvalidierung jedoch eine Tendenz, Bandbreitenwerte zu klein zu schätzen und ERFs zu erzeugen, deren Kurven zu ausgeprägt sind.
• Manuell: Der benutzerdefinierte Bandbreitenwert im Parameter Bandbreite wird verwendet. Diese Option wird empfohlen, wenn die anderen Optionen Bandbreitenwerte ergeben, die zu ERFs mit einer zu ausgeprägten Glättung oder Kurve führen. Prüfen Sie in diesem Fall die Bandbreitenwerte, die von den anderen Methoden geschätzt wurden, und nehmen Sie ggf. Korrekturen vor, um die Glättung anzupassen.

Der geschätzte Bandbreitenwert wird am Ende der Meldungen ausgegeben.

Hinweis:

Wenn bei den Methoden "Plug-in" und "Kreuzvalidierung" der geschätzte Bandbreitenwert kleiner ist als die größte Lücke zwischen Expositionswerten, wird stattdessen die größte Lücke geschätzt. Dadurch wird sichergestellt, dass jeder Expositionswert über ausreichend Daten für den gewichteten Durchschnitt verfügt. Zur Verwendung kleinerer Bandbreitenwerte müssen Sie manuell einen Bandbreitenwert angeben.

Schätzen lokaler kausaler Effekte

Sie können lokale ERFs für jeden Datensatz im Ausgabe-Feature oder in der Ausgabetabelle erstellen, indem Sie den Parameter Exposure-Response-Funktion-Pop-ups aktivieren aktivieren. Die Ausgabe enthält dann ein ERF-Diagramm in den Pop-ups der einzelnen Ausgabe-Feature- oder Ausgabetabellendatensätze. In den Pop-ups wird angezeigt, wie die Ergebnisvariable einer einzelnen Beobachtung geschätzt wird, um auf Änderungen bei der zugrunde liegenden Expositionsvariable zu reagieren. Die lokale ERF nimmt dieselbe Form wie die globale ERF an, sie wird jedoch nach oben oder unten verschoben, sodass sie durch die einzelne Beobachtung verläuft. Wenn Zielergebnis- oder Zielexpositionswerte vorhanden sind, werden diese außerdem zusammen mit den Änderungen, die bei der Exposition oder dem Ergebnis zum Erreichen der Ziele erforderlich sind, in den Pop-up-Diagrammen angezeigt.

Zum Erstellen lokaler ERFs oder Verwenden von Zielexpositions- oder Zielergebniswerten muss zusätzlich angenommen werden, dass es einen festen Expositionseffekt für alle Beobachtungen gibt. Dabei handelt es sich um eine wichtige Annahme, deren Verletzung zu verzerrten oder irreführenden Ergebnissen führen kann. Die Annahme eines festen Expositionseffekts impliziert, dass der Effekt der Exposition auf das Ergebnis für alle Individuen der Grundgesamtheit konstant ist. Das bedeutet in anderen Worten, dass bei einer bestimmten Startexposition das Ergebnis bei einer Erhöhung der Exposition um einen festen Betrag für alle Beteiligten die gleiche Ergebnisänderung zur Folge hat, und zwar unabhängig von den Werten der anderen Variablen (beispielsweise Störfaktoren). Durch die Erhöhung der Düngermenge von 150 Pfund auf 175 Pfund pro Acre müsste dann der Maisertrag auf allen Farmen um die gleiche Menge zunehmen, unabhängig vom aktuellen Maisertrag, der Bodenart, den Bewirtschaftungsmethoden oder anderen konfundierenden Variablen.

Die Annahme ist begründet, wenn keine Effektmodifikatoren vorliegen, d. h., es gibt keine Variablen, die sich darauf auswirken, wie das Ergebnis auf die Exposition auf einem individuellen Niveau reagiert. Soziodemografische Variablen wie Geschlecht, ethnische Zugehörigkeit oder das Bildungsniveau wirken jedoch oft als Effektmodifikatoren und sind normalerweise als konfundierende Variablen in Modellen der kausalen Inferenz vorhanden. Dies ist gut geeignet, um den Durchschnitt des Effekts der Modifikation auf allen Stufen der modifizierenden Variable zu ermitteln, und ermöglicht die Schätzung eines globalen kausalen Durchschnittseffekts (die ERF). Die globale ERF stellt jedoch keine spezifische Untergruppe dar, die von den Stufen des Effektmodifikators definiert wird. Beispielsweise werden in einem Berufsfortbildungsprogramm möglicherweise mehr Stellenangebote ermöglicht, wenn die Anzahl der Fortbildungsstunden erhöht wird. Die Anzahl der Stellenangebote stagniert nach einer bestimmten Anzahl von Fortbildungsstunden in Stadtteilen mit vorwiegend schwarzer oder hispanischer Bevölkerung jedoch, was potenziell auf systemische Diskriminierung bei der Einstellung zurückzuführen ist. Deshalb kann die globale ERF unbeabsichtigt Ungleichheiten, mit denen sich diese Communities konfrontiert sehen, verschleiern. Die globale ERF stellt den Effekt der Exposition auf die Durchschnittsergebnisse einer Grundgesamtheit dar. Wenn effektmodifizierende Variablen vorliegen, repräsentiert die globale ERF den Effekt der Exposition auf Ergebnisse in Stadtteilen mit vorwiegend schwarzer oder hispanischer Bevölkerung jedoch möglicherweise nicht genau.

Lokale ERFs sind nicht gültig, wenn das Modell Effektmodifikatoren enthält. Eine Möglichkeit im Umgang mit den Effektmodifikatoren ist eine Schichtung, bei der die Beobachtungen auf Grundlage der Werte der modifizierenden Variable in Schichten (oder Untergruppen) eingeteilt werden. Durch die Trennung der Effektmodifikatoren in Schichten und die Erstellung unabhängiger ERFs für jede Schicht können Sie die Beziehung zwischen der Exposition und dem Ergebnis in jeder Gruppe einzeln untersuchen. Auf diese Weise können Sie feststellen, ob der Effekt der Exposition auf das Ergebnis sich in den verschiedenen Stufen des Effektmodifikators unterscheidet.

Bootstrap-Konfidenzintervalle

Mit dem Parameter Bootstrap-Konfidenzintervalle erstellen können Sie 95-Prozent-Konfidenzintervalle für die ERF erstellen. Wenn sie erstellt werden, werden die Konfidenzintervalle als gestrichelte Linien oberhalb und unterhalb der ERF im Scatterplot und in den Meldungen angezeigt. Wenn eine ERF-Ausgabetabelle erstellt wird, enthält sie auch Felder der oberen und unteren Konfidenzgrenzen.

95-Prozent-Konfidenzintervalle werden oberhalb und unterhalb der ERF als gestrichelte Linien angezeigt.

Die Konfidenzintervalle sind Grenzen für den Bevölkerungsdurchschnitt der Ergebnisvariable für einen bestimmten Wert der Expositionsvariable. Da Bevölkerungsdurchschnittswerte eine geringere Variabilität als einzelne Mitglieder der Bevölkerung haben, liegen die meisten Punkte des Scatterplots im Allgemeinen nicht in den Konfidenzintervallen. Dies stellt jedoch kein Problem dar. Aus ähnlichen Gründen gelten die Konfidenzintervalle nur für die globale ERF und können nicht auf lokale ERFs angewendet werden.

Die Konfidenzintervalle werden mit M-out-of-N-Bootstrapping erstellt. Bei dieser Vorgehensweise werden willkürlich M Beobachtungen aus den N Beobachtungen als Referenz erfasst. Dabei gilt M=2*sqrt(N), wie von DasGupta (2008) empfohlen. Danach führt das Werkzeug den gesamten Algorithmus (Suche nach optimalen Parametern, Wahrscheinlichkeits-Score-Schätzung, Ausgleichstest und ERF-Schätzung) für die willkürliche Bootstrap-Stichprobe aus. Die resultierende ERF ist normalerweise ähnlich wie die ursprüngliche ERF, jedoch nicht identisch. Durch die häufige Wiederholung dieses Vorgangs können Sie ermitteln, wie stark die ERF bei verschiedenen willkürlichen Stichproben der Beobachtungen variiert. Die Variation der resultierenden ERFs fördert die Erstellung der Konfidenzintervalle.

Wenn für eine Bootstrap-Stichprobe kein Ausgleich gemäß dem angegebenen Ausgleichstyp und Ausgleichsschwellenwert erreicht werden kann, wird diese verworfen. Das Bootstrapping wird vom Werkzeug fortgesetzt, bis 5*sqrt(N) Bootstrap-Stichproben ausgeglichen werden konnten. Dieser Wert wird abgeleitet, sodass jede Beobachtung im Durchschnitt erwartungsgemäß in mindestens 10 ausgeglichenen Bootstrap-Stichproben enthalten ist. Auf diese Weise sind stabile Schätzungen der oberen und unteren Grenze über den gesamten Expositionsbereich möglich. Wenn nach 25*sqrt(N) Bootstrapping-Versuchen weiterhin nicht genügend ausgeglichene Bootstraps vorhanden sind, werden die Konfidenzintervalle nicht erstellt und es wird eine Warnmeldung zurückgegeben.

Über die Konfidenzintervalle lassen sich viele Unsicherheitsquellen der ERF erfassen. Es ist jedoch wichtig anzumerken, dass alle potenziellen Unsicherheitsquellen berücksichtigt sein müssen, damit Konfidenzintervalle erstellt werden können, die tatsächlich der oberen und unteren Grenze des kausalen Effekts entsprechen. Beim Bootstrapping-Verfahren in diesem Werkzeug wird die Unsicherheit beim Ausgleich und der ERF-Schätzung mit einbezogen, andere mögliche Unsicherheitsquellen können jedoch nicht berücksichtigt werden, z. B. Ungenauigkeit bei den Variablenwerten oder die Wahl der ERF-Funktionsform (z. B. ein gewichteter gleitender Durchschnitt im Gegensatz zu einem Spline oder einer globalen Polynominterpolation). Darüber hinaus können die Konfidenzintervalle beliebig schmal werden, wenn Sie die Anzahl der Beobachtungen erhöhen. Das bedeutet jedoch nicht, dass es sich bei der ERF um eine perfekte Charakterisierung des kausalen Effekts handelt.

Wenn Bootstrap-Konfidenzintervalle erstellt werden, enthalten die Ausgabe-Features oder -Tabelle zwei Felder im Zusammenhang mit den Bootstraps. Im ersten Feld wird angegeben, wie oft die Beobachtung in einer Bootstrap-Stichprobe ausgewählt wurde, im zweiten Feld, wie oft die Beobachtung in einer Bootstrap-Stichprobe vorkam, die ausgeglichen werden konnte und für die ein ERF geschätzt wurde. Diese Felder werden auch dann erstellt, wenn nicht genügend Bootstrap-Stichproben ausgeglichen werden konnten, um Konfidenzintervalle zu schätzen. Die Werte der ersten Spalte von Ausgabe-Features zeigen wenige räumliche Muster außer an den Rändern der Features. Wenn jedoch räumliche Muster im zweiten Feld angegeben werden, kann dies darauf hinweisen, dass ein räumlicher Prozess nicht berücksichtigt wurde. Wenn beispielsweise die meisten ausgeglichenen Bootstrap-Stichproben aus bestimmten Datenregionen stammen, sind diese Regionen in den Konfidenzintervallen überrepräsentiert und die Intervalle können unrealistisch schmal sein. Wenn Sie räumliche Muster in der Anzahl der ausgeglichenen Bootstrap-Stichproben erkennen, erwägen Sie, eine räumliche konfundierende Variable hinzuzufügen (z. B. eine geographische Region), um den fehlenden räumlichen Effekt miteinzubeziehen.

Bei Eingabetabellen wählt jedes Bootstrap M Beobachtungen zufällig und gleichmäßig aus. Die Stichproben werden danach erneut zur Auswahl zur Verfügung gestellt, sodass eine Beobachtung im selben Bootstrap mehrere Male ausgewählt werden kann. Bei einer Feature-Eingabe werden die Bootstrap-Stichproben generiert, indem ein einziges Feature zufällig ausgewählt und das Feature sowie seine acht benachbarten Features in die Stichprobe aufgenommen werden. Diese willkürliche Auswahl wird wiederholt, nachdem das Feature wieder für die Auswahl verfügbar gemacht wurde, bis mindestens M Beobachtungen in der Bootstrap-Auswahl enthalten sind. Dieselben Features können mehrmals willkürlich ausgewählt und mehrmals als Nachbarn hinzugefügt werden. Die Verwendung zufälliger Nachbarschaften anstelle einer vollständig zufälligen Auswahl erleichtert die Korrektur räumlicher Störfaktoren, zu denen keine Messungen vorliegen. (Es empfiehlt sich dennoch, räumliche Störfaktoren zu korrigieren, indem Sie räumliche Variablen als konfundierende Variablen einbeziehen.)

Da ERFs nicht über den Bereich der Expositionswerte, mit denen sie erstellt wurden, hinausreichen können, wird die ERF der einzelnen Bootstrap-Stichproben nur zwischen der minimalen und maximalen Exposition der Beobachtungen in der zufälligen Stichprobe erstellt. Das bedeutet, dass sich die höchsten und niedrigsten Expositionswerte häufig nicht innerhalb des Bereichs der zufällig als Stichprobe genommenen Werte befinden, weshalb weniger Bootstrapping-ERFs für die extremsten Expositionswerte erstellt werden.

Nachdem alle Bootstraps durchgeführt wurden, werden die 95-Prozent-Konfidenzintervalle erstellt, indem eine T-Verteilung der Bootstrap-ERF-Werte für jeden Expositionswert angenommen wird. Die Varianz der ERF-Werte wird neu skaliert, indem mit (M/N) multipliziert wird, um nur die M-Werte der erfassten Stichproben zu bereinigen. Der Grad der Freiheit entspricht der Anzahl von Bootstrap-ERFs, die für den Expositionswert generiert werden könnten, minus eins. Darüber hinaus wird die Breite der Konfidenzintervalle mit demselben Kernel-Glätter geglättet, der zum Schätzen der ursprünglichen ERF (gleiche Gewichtungen mit Plug-in-Bandbreite) verwendet wurde. Die geglättete Breite wird dann addiert und von der ursprünglichen ERF subtrahiert, um die oberen und unteren Konfidenzgrenzen zu erzeugen. Wenn eine Ausgabe-ERF-Tabelle erstellt wird, enthält sie Felder mit der geglätteten Standardabweichung (geglättete Breite geteilt durch kritischen Wert) und die Anzahl der Bootstrap-ERFs, die für den Expositionswert generiert werden könnten.

Referenzen

Bei der Implementierung des Werkzeugs wurden folgende Ressourcen verwendet:

• DasGupta, Anirban. 2008. "Asymptotic Theory of Statistics and Probability." New York, NY. Springer. ISBN 978-0-387-75971-5. https://doi.org/10.1007/978-0-387-75971-5.

• Fan, Jianquin. 1996. "Local Polynomial Modeling and Its Applications: Monographs on Statistics and Applied Probability 66." (1. Aufl.). Routledge. https://doi.org/10.1201/9780203748725.

• Imbens, Guido und Rubin, Donald B. 2015. "Causal Inference for Statistics, Social, and Biomedical Sciences: An Introduction." Cambridge: Cambridge University Press. https://doi.org/10.1017/CBO9781139025751.

• Khoshnevis, Naeem; Wu, Xiao und Braun, Danielle. 2023. "CausalGPS: Matching on Generalized Propensity Scores with Continuous Exposures." R-Paketversion 0.4.0. https://CRAN.R-project.org/package=CausalGPS.

• Wu, Xiao; Mealli, Fabrizia; Kioumourtzoglou, Marianthi-Anna; Dominici, Francesca und Braun, Danielle. 2022. "Matching on Generalized Propensity Scores with Continuous Exposures." Journal of the American Statistical Association. https://doi.org/10.1080/01621459.2022.2144737.