Berechnen des Konsistenzverhältnisses für paarweisen Vergleich

Mit dem Werkzeug Gewichtungen durch paarweisen Vergleich zuweisen werden die relativen Gewichtungen für verschiedene Eingabevariablen berechnet, indem sie paarweise verglichen werden. Durch eine Diagnosefunktionalität wird sichergestellt, dass die Vergleichsbewertungen aller Paare logisch konsistent sind. Das Werkzeug berechnet das Konsistenzverhältnis (Consistency Ratio, CR), mit dessen Hilfe Sie die Konsistenz von Bewertungen verbessern können. Paarweise Bewertungen sind beispielsweise inkonsistent, wenn Sie die Variable A als zweimal so wichtig wie Variable B, Variable B als zweimal so wichtig wie Variable C und Variable C als genauso wichtig wie Variable A einstufen. Das heißt, wenn A > B und B > C, dann kann C nicht gleich A sein.

Indem Sie dafür sorgen, dass der CR-Wert innerhalb akzeptabler Grenzen liegt, können Sie inkonsistente Rangstufen verhindern. Gemäß Saaty (2000) gilt Folgendes:

• Wenn CR <= 0,1, ist die Konsistenz des paarweisen Vergleichs akzeptabel.
• Wenn CR > 0,1, sollten die Vergleichsbewertungen angepasst werden, um die Konsistenz zu verbessern.

Prozess für die Berechnung des Konsistenzverhältnisses

Der CR-Wert wird mit den folgenden Schritten berechnet:

• Der Konsistenzindex (Consistency Index, CI) wird berechnet.
• Der Zufallsindex (Random Index, RI) wird basierend auf der Anzahl der Variablen ermittelt.
• Der CR-Wert wird durch Dividieren des CI-Wertes durch den RI-Wert berechnet.

Die folgende Vergleichsmatrix veranschaulicht als Beispiel die Berechnung des CR-Wertes für fünf Variablen.

Tabelle 1: Vergleichsmatrix mit abgeleiteten Gewichtungen.

Variable	Solar_Gain	Aspect	Elevation	Dist_to_Road	Dist_to_Elect	Weights
Solar_Gain	1	3	2	2	0,333	0,235
Aspect	0,333	1	0,5	1	0,2	0,089
Elevation	0,5	2	1	1	0,5	0,136
Dist_to_Road	0,5	1	1	1	5	0,247
Dist_to_Elect	3	5	2	0,2	1	0,294

In den Berechnungen werden die nachstehend beschriebenen Gleichungen verwendet.

Berechnen des CI-Wertes

Der CI-Wert wird mit der folgenden Formel berechnet:

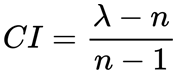
Wobei gilt:

• λ (der Haupteigenwert) ist der Durchschnitt von λ_i für jede Variable
• n ist die Anzahl der Eingabevariablen

Der λ_i-Wert für jede Variable wird mit der folgenden Formel berechnet:

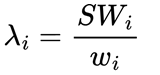
Wobei gilt:

• w_i gibt die abgeleiteten Gewichtungen für jede Eingabevariable an (Spalte "Gewichtungen" in Tabelle 1)
• SW_i ist die gewichtete Summe für jede Variable i

Die gewichtete Summe für jede Variable wird mit der folgenden Formel berechnet:

Wobei gilt:

• a_ij ist der Wert aus der ursprünglichen Matrix für paarweisen Vergleich, wobei sich i auf die Zeile und j auf die Spalte bezieht
• wj sind die abgeleiteten Gewichtungen der entsprechenden Variablen

Der SW-Wert für die Variablenzeile "Solar_Gain" wird beispielsweise wie folgt berechnet:

Der λ_i-Wert für die Variable "Solar_Gain" wird wie folgt berechnet:

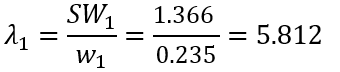
Wiederholen Sie die Berechnungen für jede Zeile, um den λ_i-Wert für jede Variable zu ermitteln.

Bilden Sie als Nächstes den Durchschnitt der λ_i-Werte, um λ zu erhalten.

In diesem Beispiel ist λ wie unten in der Tabelle angegeben 6,462.

Tabelle 2: Berechnung der gewichteten Summe (SW) und des λ_i-Wertes für jede Variable.

Variable	Weights(wi)	Weighted Sum(SWi)	λi = SWi / wi
Solar_Gain	0,235	1,366	5,812
Aspect	0,089	0,541	6,079
Elevation	0,136	0,826	6,070
Dist_to_Road	0,247	2,060	8,338
Dist_to_Elect	0,294	1,765	6,005
Average	Nicht zutreffend	Nicht zutreffend	6,462

Nachdem λ berechnet ist, kann CI mit der oben genannten Formel berechnet werden.

Da die Anzahl der Variablen in diesem Beispiel fünf beträgt, wird der Wert für CI wie folgt berechnet:

CI = (6,462 - 5)/(5 - 1) = 0,365

Berechnen des RI-Wertes

RI ist ein vordefinierter statistischer Wert, der als Bezugswert für die Berechnung des CR-Wertes für paarweise Vergleiche dient. Die von Saaty (2000) erarbeiteten RI-Werte werden von einer Monte-Carlo-Simulation für jede Matrixgröße abgeleitet. Die abgeleiteten RI-Werte für jede Matrixgröße sind in der folgenden Tabelle aufgeführt. Die Matrixgrößen werden in der obersten Zeile identifiziert.

Matrixgröße	2	3	4	5	6	7	8	9
RI	0	0,58	0,90	1,12	1,24	1,32	1,41	1,45

Der RI-Wert ist für den Vergleich von zwei Variablen gleich 0, da der Vergleich inhärent konsistent ist. Die RI-Werte steigen mit der Anzahl der Eingabevariablen.

In diesem Beispiel beträgt die Anzahl der Variablen fünf, daher lautet der entsprechende RI-Wert 1,12.

Berechnen des CR-Wertes

Der CR-Wert wird durch Dividieren des CI-Wertes durch den RI-Wert berechnet. Aus diesem CR-Wert geht hervor, wie konsistent die paarweisen Vergleiche sind.

In diesem Beispiel wird der CR-Wert wie folgt berechnet:

CR = 0,365/1,12 = 0,326

Da der CR-Wert größer als 0,1 ist, sollten Sie die Vergleichsbewertungen ändern, um die Konsistenz zu verbessern.

Verbessern der Konsistenz

Wenn die Vergleiche der Eingabevariablen inkonsistent sind, werden die drei Paare, die am meisten zur Inkonsistenz beitragen, markiert. Die markierten Paare sollten angepasst werden, um die Konsistenz zu verbessern.

Mit dem folgenden Workflow werden die drei Paare mit der größten Inkonsistenz ermittelt.

Erstellen einer Matrix für paarweise Konsistenz

Erstellen Sie eine Matrix, die bei der paarweisen Konsistenzbewertung (Saaty, 2003) verwendet werden soll. Diese Matrix wird in der folgenden Formel als ε_ij bezeichnet:

Wobei gilt:

• a_ij ist der Wert aus der ursprünglichen Matrix für paarweisen Vergleich, i bezieht sich auf die Zeile und j auf die Spalte.
• w_j und w_i sind die abgeleiteten Gewichtungen für die Variablen j und i.

Berechnen der Werte

Nachdem die Matrix erstellt wurde, werden die drei größten Werte in der Matrix ε_ij identifiziert. Die entsprechenden Zeilen- und Spaltenvariablen gelten als inkonsistente Paare.

In diesem Vergleichsbeispiel ist der CR-Wert größer als 0,1 (0,326). Zum Identifizieren der inkonsistenten Paare wird der ε_ij-Wert für die Zeile "Solar_Gain" und die Spaltenzelle "Ausrichtung" wie folgt berechnet:

Wiederholen Sie die Berechnung für alle Zellen.

Ermitteln der Paare mit der größten Inkonsistenz

Die ε_ij-Matrix für das oben gezeigte Vergleichsbeispiel wird wie folgt erstellt:

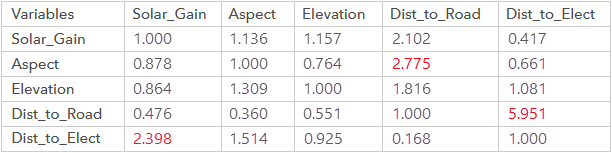
Die drei höchsten Werte in der Matrix sind die Vergleiche, die am meisten zur Inkonsistenz beitragen. Dabei handelt es sich um die Vergleichsbewertungen für die Variablen "Dist_to_Road" und "Dist_to_Elect", für die Variablen "Ausrichtung" und "Dist_to_Road" sowie für die Variablen "Dist_to_Elect" und "Solar_Gain". Die drei Paare sind auf beiden Seiten der Schieberegler im Dialogfeld des Werkzeugs rot markiert.

In der ursprünglichen Vergleichsmatrix wird die Variable "Solar_Gain" als zweimal so wichtig wie "Dist_to_Road" (Solar_Gain > Dist_to_Road) und dreimal weniger wichtig als "Dist_to_Elect" (Dist_to_Elect > Solar_Gain) bewertet. Logischerweise sollte "Dist_to_Road" weniger wichtig sein als "Dist_to_Elect" (Dist_to_Elect > Dist_to_Road). Im ursprünglichen Vergleich jedoch wurde bei der Bewertung fälschlich "Dist_to_Road" eine fünfmal so hohe Gewichtung wie "Dist_to_Elect" (Dist_to_Road > Dist_to_Elect) zugewiesen. Dies ist eine Hauptursache der Inkonsistenz.

Um sie zu beheben, verschieben Sie den Schieberegler in Richtung "Dist_to_Elect", und überprüfen Sie den CR-Wert erneut. Wenn Sie zum Beispiel den Schieberegler auf Position 5 auf der Seite von "Dist_to_Elect" verschieben und erneut auf die Schaltfläche Konsistenz klicken, lautet der neue CR-Wert 0,029. Dies bedeutet, dass der Vergleich jetzt insgesamt konsistent ist.

Referenzen

Saaty, T. L. 2000. Fundamentals of Decision Making and Priority Theory with the Analytic Hierarchy Process. Pittsburgh, PA: RWS Publications

Saaty, T. L. 2003. "Decision-making with the AHP: Why is the principal eigenvector necessary". European Journal of Operational Research, 145(1), 85-91.