Mithilfe des Werkzeugs Abschnittsgrößen für die Punktaggregation auswerten können Sie beim Aggregieren von Punktanzahlen in quadratischen oder hexagonalen Abschnitten, die als Mosaik angeordnet sind, eine geeignete Abschnittsgröße auswählen. Außerdem können Sie mit dem Werkzeug verschiedene andere Abschnittsgrößen bewerten, um zu ermitteln, wie sich die resultierenden Anzahlen und Muster bei Verwendung anderer Abschnittsgrößen verändern würden.
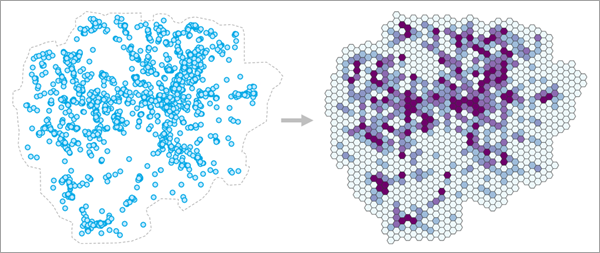
Das Aggregieren und Zählen von Punkten in Abschnitten, beispielsweise das Aggregieren von Notrufen, Serviceausfällen und Tiersichtungen, ist ein gängiger GIS-Workflow. Es wird auch verwendet, um große Punktgruppen besser sichtbar zu machen und den Datenschutz zu gewährleisten, indem einzelne Punktpositionen unkenntlich gemacht werden. Trotz der vielen Anwendungsmöglichkeiten gibt es jedoch relativ wenige Richtlinien dafür, wie groß diese Abschnitte sein sollten. In der Praxis werden die Abschnittsgrößen oft danach ausgewählt, was am einfachsten ist (z. B. Verwendung einer runden Zahl), oder danach, welche Abschnittsgröße die optisch ansprechendsten Ergebnisse liefert. Die Wahl des Maßstabs beeinflusst jedoch sowohl das, was Sie erkennen können, als auch die Interpretation (ein Beispiel für das "Modifiable Areal Unit Problem"). Daher ist es wichtig, begründbare und reproduzierbare Entscheidungen zu treffen. Wichtig ist auch, dass Sie charakterisieren, wie stark die resultierenden Punktanzahlen von der Abschnittsgröße beeinflusst werden: Würde die Verwendung größerer oder kleinerer Abschnitte zu anderen Mustern und Schlussfolgerungen führen?
Grundsätzlich ist die Bestimmung einer geeigneten Abschnittsgröße für die Aggregation von Punktdaten in Abschnitten ein Maßstabsproblem. Zu kleine Abschnitte sind größtenteils leer und weisen stark schwankende Anzahlen auf, während zu große Abschnitte wichtige lokale Muster verschleiern und maskieren. Eine geeignete Abschnittsgröße ist groß genug, um variierende Punktanzahlen (anstelle von vielen leeren Abschnitten mit wenigen großen Anzahlen) zu erzeugen, aber dennoch klein genug, dass lokale Punktmuster in den resultierenden Abschnitten erhalten bleiben (anstatt durch Aggregation eliminiert zu werden).
Zum Bestimmen einer geeigneten Abschnittsgröße wird eine Reihe von Größenkandidaten anhand von zwei Kriterien ausgewertet: interne Einheitlichkeit und Varianz der Punktanzahlen. Mit dem Kennwert der internen Einheitlichkeit wird gemessen, ob die Punkte in den einzelnen Abschnitten räumlich zufällig auftreten. Bevorzugt werden fast immer kleinere Abschnittsgrößen. Mit dem Kennwert der Varianz der Punktanzahlen dagegen wird gemessen, wie gleichmäßig verteilt die resultierenden Abschnitte sind. Hierbei werden fast immer größere Abschnittsgrößen bevorzugt.

Diese beiden Kennwerte (jeweils Werte zwischen 0 und 1) werden dann miteinander multipliziert, sodass sich für jede Abschnittsgröße ein einziges Auswertungsergebnis ergibt. Das Werkzeug empfiehlt die Abschnittsgröße mit dem höchsten Auswertungsergebnis. Der Kurve für die Auswertungsergebnisse können Sie auch entnehmen, wie andere Abschnittsgrößen im Vergleich zur empfohlenen Abschnittsgröße bewertet wurden.

Weitere Informationen zu Auswertungsergebnissen und ihrer Berechnung finden Sie weiter unten im Abschnitt Zusätzliche Details zur Auswertung von Abschnittsgrößen.
Definieren einer geeigneten Aggregationsgrenze
Sie müssen nicht nur die zu aggregierenden Punkte angeben, sondern auch mit dem Parameter Aggregationsgrenze die Fläche definieren, in der die Punkte aggregiert und Abschnitte erstellt werden sollen. Die Aggregationsgrenze (die auch manchmal als Untersuchungsgebiet oder Interessenbereich bezeichnet wird) sollte die Fläche definieren, in der Punkte vorkommen und aufgezeichnet werden können. Wenn beispielsweise Notrufe innerhalb einer Stadt aggregiert werden, sollte die Stadtgrenze als Aggregationsgrenze verwendet werden, da ein Notruf von überall innerhalb der Stadt kommen kann. Anrufe von außerhalb der Stadt würden nicht in den Datensatz einbezogen. Es ist zwar verlockend, sich vorzustellen, dass die Abschnitte erstellt und dann auf die Aggregationsgrenze zugeschnitten werden, doch hat die Grenze vielmehr einen starken Einfluss auf die Auswertungsergebnisse und die empfohlene Abschnittsgröße. Die Auswahl einer nicht geeigneten Aggregationsgrenze führt häufig zu unrealistisch großen oder kleinen empfohlenen Abschnittsgrößen. Daher sollten Sie unbedingt abwägen, welche Grenze für die Daten am besten geeignet ist.
Durch Angabe einer Grenze festzulegen, welche Punkte auftreten bzw. nicht auftreten können, ist wichtig, da das Werkzeug unterscheiden können muss, ob eine Fläche keine Punkte aufweist, weil dort keine Ereignisse stattgefunden haben (z. B. ein Stadtteil, in dem es in einer bestimmten Woche keine Raubüberfälle gegeben hat), oder ob es nicht möglich ist, in dieser Fläche Punkte zu beobachten (z. B. Walbeobachtungen an Land). Da das Werkzeug die Varianz der resultierenden Punktanzahlen in den Abschnitten bewertet, sind Anzahlen gleich Null ebenso wichtig wie alle anderen Anzahlen. Abschnittsgrößen, die zu einem hohen Anteil von Abschnitten ohne Punkte führen, werden vermieden. In der Praxis bedeutet dies, dass bei einer zu großen Aggregationsgrenze (d. h. einer mit vielen Flächen, in denen keine Punkte erfasst werden können), eine unrealistische Abschnittsgröße empfohlen wird, um die Lücken zu füllen und die Anzahl der leeren Abschnitte zu reduzieren. Bei einem zu kleinen Untersuchungsgebiet hingegen werden kleinere Abschnittsgrößen empfohlen, um die Anzahl der Abschnitte ohne Punkte zu erhöhen.
Wenn eine geeignete Aggregationsgrenze für den Punkt bekannt ist (beispielsweise eine Stadtgrenze), wählen Sie die Option Benutzerdefinierte Polygone aus, und geben Sie die Grenze im Parameter Benutzerdefinierte Polygone an. Sie können die Aggregationsgrenze auch mit Interaktive Feature-Eingabe interaktiv zeichnen.
Wenn keine geeignete Aggregationsgrenze bekannt ist, kann die Grenze mit der Option Konkave Hülle, Konvexe Hülle oder Envelope automatisch erstellt werden (weitere Informationen finden Sie unter Minimale Begrenzungsgeometrie). Bei Verwendung einer automatisch erstellten Grenze sollten Sie immer visuell beurteilen, ob die Grenze die Punkte adäquat darstellt. Wenn die Grenze nicht geeignet ist, verwenden Sie eine andere Option, oder zeichnen Sie interaktiv eine Grenze, die die Punkte besser darstellt.
Die folgende Abbildung zeigt die resultierenden Abschnittsgrößen für die gleichen Daten mit allen Optionen des Parameters Aggregationsgrenze. Bei der benutzerdefinierten Option wird die tatsächliche Grenze verwendet, innerhalb derer die Punkte erfasst wurden. Bei anderen Datasets (insbesondere solchen mit räumlichen Ausreißern) können die Unterschiede bei den resultierenden Abschnittsgrößen und Mustern noch extremer sein.

Werkzeugausgaben
Das Werkzeug erstellt drei Ausgaben, die in einem Gruppen-Layer enthalten sind. Die primäre Ausgabe ist eine Polygon-Feature-Class der aggregierten Abschnitte mit der empfohlenen Abschnittsgröße. Der Layer wird durch die Punktanzahlen in den einzelnen Abschnitten symbolisiert.
Die zweite Ausgabe ist eine Polygon-Feature-Class der vom Werkzeug verwendeten Aggregationsgrenze. Diese Ausgabe ist am nützlichsten für die Optionen "Konkave Hülle" und "Konvexe Hülle", um die Formen der Grenzen zu sehen. Die dritte Ausgabe ist eine Tabelle, in der sich die Auswertungsergebnisse für alle vom Werkzeug getesteten Abschnittsgrößen befinden. Die Tabelle verfügt über zwei Diagramme, die zum Untersuchen der Abschnittsgrößen verwendet werden können.
Diagramm "Auswertungsergebnisse in allen Abschnittsgrößen"
Das Diagramm Auswertungsergebnisse in allen Abschnittsgrößen zeigt die Auswertungsergebnisse für alle getesteten Abschnittsgrößen an. Die blauen Punkte im Diagramm stellen die unverarbeiteten Auswertungsergebnisse für die Abschnittsgrößen dar. Sie wurden mit einem Spline (der blauen Kurve) geglättet. Der größte Wert der blauen Kurve ist die empfohlene Abschnittsgröße. Er ist mit einer vertikalen orangefarbenen Linie gekennzeichnet. Außerdem wird um die empfohlene Abschnittsgröße herum ein heller orangefarbener Konfidenzbereich angezeigt. Alle Abschnittsgrößen in diesem Bereich haben ein Auswertungsergebnis, das nicht signifikant niedriger als die empfohlene Abschnittsgröße ist. Sie können also einen beliebigen Wert (z. B. eine runde Zahl) in diesem Bereich auswählen, ohne dass sich das Auswertungsergebnis signifikant verringert.

Die empfohlene Abschnittsgröße und die zugehörige Fläche jedes Abschnitts werden unten im Diagramm angezeigt. Bei Quadratabschnitten entspricht die Abschnittsgröße der Breite oder Höhe jedes Quadrats. Bei Hexagonen entspricht sie der Höhe jedes Hexagons (dem Abstand zwischen der flachen Kante und der gegenüberliegenden flachen Kante).
Hinweis:
Die kleinste getestete Abschnittsgröße (der Minimalwert der X-Achse) ist die Abschnittsgröße, die zu 20 Abschnitten für jeden Eingabepunkt führt. (Mit anderen Worten: Die Abschnitte sind so klein, dass mehr als 95 Prozent von ihnen keine Punkte enthalten.). Die größte Abschnittsgröße (der Maximalwert der X-Achse) entspricht 25 Prozent der X- oder Y-Ausdehnung, je nachdem, was größer ist. Das Werkzeug testet 100 Abschnittsgrößen, die gleichmäßig zwischen Minimum und Maximum inkrementiert wurden.
Diagramm "Interne Einheitlichkeit und Varianz der Punktanzahl in allen Abschnittsgrößen"
Das Diagramm Interne Einheitlichkeit und Varianz der Punktanzahl in allen Abschnittsgrößen zeigt die zwei Kriterien an, die kombiniert wurden, um die Auswertungsergebnisse zu erhalten. Für jede getestete Abschnittsgröße zeigt eine grüne Kurve das Ergebnis für die interne Einheitlichkeit und eine violette Kurve das Ergebnis für die Varianz der Punktanzahl an. Normalerweise nimmt die grüne Kurve ab und die violette Kurve zu. Zu Kontextzwecken werden außerdem die empfohlene Abschnittsgröße und das Konfidenzintervall angezeigt. Die empfohlene Abschnittsgröße weist in der Regel für beide Kriterien angemessene Ergebnisse auf, was auf ein ausgewogenes Verhältnis zwischen den gegensätzlichen Kriterien hindeutet. Weitere Informationen zu den einzelnen Kriterien finden Sie weiter unten im Abschnitt Zusätzliche Details zur Auswertung von Abschnittsgrößen.

Geoverarbeitungsmeldungen
Die Meldungen des Werkzeugs enthalten einen Abschnitt Ergebniszusammenfassung und einen Abschnitt Aggregationszusammenfassung. In der Ergebniszusammenfassung werden die empfohlene Abschnittsgröße und die zugehörige Abschnittsfläche angezeigt. Für Hexagone wird außerdem die Seitenlänge jedes Hexagons angezeigt. Die Aggregationszusammenfassung enthält verschiedene Summenstatistiken der resultierenden Abschnitte und Punktanzahlen, beispielsweise die Anzahl der Punkte, die Anzahl der Abschnitte, die mittlere Punktanzahl und die Fläche der Aggregationsgrenze.
Empfehlungen und Beschränkungen
Bei der Verwendung des Werkzeugs gelten die folgenden Empfehlungen und Beschränkungen:
Das Werkzeug nimmt an, dass eine einzige Abschnittsgröße für die Aggregation von Punkten geeignet ist. In vielen Fällen gibt es jedoch nicht die eine einzige Abschnittsgröße, die die Punkte entlang der gesamten Aggregationsgrenze adäquat darstellt. So kann es zum Beispiel in einem großen Landkreis mit ländlichen Gebieten und geringer Bevölkerungsdichte sowie städtischen Gebieten mit hoher Bevölkerungsdichte schwierig sein, Notrufe für den gesamten Landkreis zu aggregieren. Abschnitte, die klein genug sind, um die städtischen Gebiete adäquat darzustellen, sind in ländlichen Gebieten größtenteils leer, während Abschnitte, die für ländliche Gebiete groß genug sind, städtische Ballungsräume auf einige wenige Abschnitte verdichten. Ein häufiges Anzeichen für dieses Problem sind sehr große Konfidenzintervalle um die empfohlene Abschnittsgröße herum, die auf eine hohe Unsicherheit hinsichtlich der zu verwendenden Abschnittsgröße hindeuten. Eine mögliche Lösung besteht darin, die Punkte in verschiedene Datasets aufzuteilen und sie separat mit unterschiedlichen Abschnittsgrößen zu aggregieren.
- Das Werkzeug ist am besten geeignet, wenn Sie mit den resultierenden Punktanzahlen anstelle einer einfachen kartografischen Glättung eine Analyse durchführen möchten (zum Beispiel Hot Spot-Analyse oder Lokale Ausreißeranalyse). Obwohl es zur besseren visuellen Darstellung sinnvoll sein kann, große Punktgruppen zu glätten, besteht der Hauptzweck des Werkzeugs darin, aggregierte Abschnitte zu erstellen, bei denen die räumliche Struktur der Punkte bestmöglich beibehalten wird, und für Analysen geeignete Punktzahlen zu erzeugen.
- Große Anzahlen lagegleicher Punkte (zahlreicher Punkte mit den gleichen Koordinaten) können zu unrealistischen Abschnittsgrößen führen. Das Werkzeug gibt eine Warnung zurück, wenn lagegleiche Eingabepunkte vorhanden sind.
Zusätzliche Details zur Auswertung von Abschnittsgrößen
Die allgemeine Methodik des Werkzeugs besteht darin, eine Reihe von Abschnittsgrößen anhand von zwei Kennwerten auszuwerten: interne Einheitlichkeit und Varianz der Punktanzahlen. Jede Abschnittsgröße erhält für jeden Kennwert eine Punktzahl zwischen 0 und 1. Die Werte werden miteinander multipliziert, sodass ein endgültiges Auswertungsergebnis entsteht, bei dem beide Kriterien in ausgewogenem Verhältnis stehen. Beim Kennwert der internen Einheitlichkeit werden im Allgemeinen kleinere Abschnittsgrößen bevorzugt, beim Kennwert der Varianz der Punktanzahlen dagegen größere Abschnittsgrößen. Demzufolge erhalten die höchsten Auswertungsergebnisse diejenigen Abschnittsgrößen, die in der Mitte liegen und den besten Kompromiss zwischen den gegensätzlichen Kriterien darstellen. In den folgenden Abschnitten werden die beiden Kriterien näher beschrieben.
Interne Einheitlichkeit
Mit dem Kennwert der internen Einheitlichkeit wird gemessen, ob die Punkte gleichmäßig auf die sich ergebenden Abschnitte verteilt sind. Im Beispiel in der folgenden Abbildung sind die Punkte im linken Abschnitt stark in einer Ecke geclustert, während sie im rechten Abschnitt zufällig und gleichmäßig verteilt sind. Daher ist die interne Einheitlichkeit des rechten Abschnitts höher.

Die interne Einheitlichkeit spielt eine wichtige Rolle dabei, Abschnittsgrößen zu vermeiden, bei denen wichtige lokale Muster nicht sichtbar sind. Wenn die Punkte innerhalb eines Abschnitts eine starke Cluster-Bildung oder ein ausgeprägtes Muster aufweisen, kann es irreführend sein, sie zu einer einzigen Anzahl zusammenzufassen. Für den Kennwert wird überprüft, ob die Punkte in den einzelnen Abschnitten zufällig angeordnet sind, was darauf schließen lässt, dass der Abschnitt eine gerechte und repräsentative Zusammenfassung der darin enthaltenen Punkte darstellt. Wenn viele Abschnitte strukturierte Muster aufweisen, ist dies ein Zeichen dafür, dass die Abschnittsgröße möglicherweise zu groß ist, sodass wichtige Muster innerhalb der Abschnitte nicht sichtbar sind.
Der Kennwert wird berechnet, indem die einzelnen Abschnitte auf ihre vollständige räumliche Zufälligkeit getestet werden. Der Wert entspricht dem Anteil der Abschnitte mit einem p-Wert, der größer als 0,05 ist (was bedeutet, dass keine Cluster erkannt wurden). Abschnitte ohne Punkte sind nicht in dem Anteil enthalten, da leere Zellen nicht als räumlich zufällig oder geclustert klassifiziert werden können.
Beim Test auf vollständige räumliche Zufälligkeit werden die einzelnen Abschnitte in eine Reihe kleinerer Abschnitte unterteilt. Bei Quadraten wird der Abschnitt in 25 kleinere Quadrate unterteilt, bei Hexagonen in 24 Dreiecke. Die Anzahl der Punkte innerhalb der Quadrate oder Dreiecke wird dann mit einem Chi-Quadrat-Test der Anpassungsgüte auf ihre Einheitlichkeit getestet.
Varianz der Punktanzahl
Der Kennwert der Varianz der Punktanzahlen quantifiziert die Vielfalt der Punktanzahlen in den Abschnitten und bevorzugt Abschnittsgrößen, die zu einer großen Varianz der Anzahlwerte führen. Dabei werden Abschnittsgrößen vermieden, die einen hohen Anteil an leeren Abschnitten sowie eine geringe Anzahl von Abschnitten mit hohen Anzahlen aufweisen. Konzeptionell fördert dies die Aussagekraft der Informationen und spiegelt die Idee wider, dass Aggregationen zu einer sinnvollen Variation und Vielfalt der Punktanzahlen führen sollten, was besonders dann wünschenswert ist, wenn Sie eine Analyse (beispielsweise eine Hot Spot-Analyse) der Punktanzahlen durchführen möchten. In der Praxis steigt dieser Wert tendenziell mit der Abschnittsgröße, da größere Abschnitte tendenziell vielfältigere und gleichmäßiger verteilte Anzahlen enthalten.
In der Abbildung unten beispielsweise ergeben die unteren Abschnitte eine größere Varianz und eine gleichmäßigere Verteilung der Punktanzahlen als die oberen Abschnitte, sodass die unteren Abschnitte ein höheres Ergebnis für die Varianz der Punktanzahlen erhalten würden. Im Allgemeinen gilt: Je näher die Verteilung der Punktanzahlen an einer einheitlichen (flachen) Verteilung liegt, umso höher fällt das Ergebnis aus.

Der Kennwert wird anhand eines normalisierten Shannon-Entropiemesswertes berechnet. Für jede Abschnittsgröße wird die Verteilung der Abschnittsanzahlen in fünf gleiche Intervalle unterteilt und die Entropie dieser Verteilung berechnet. Diese Entropie wird dann durch die Entropie einer einheitlichen Verteilung dividiert, wodurch sich ein Wert zwischen 0 und 1 ergibt.
Hinweis:
Die Ergebnisse für die interne Einheitlichkeit und die Varianz der Punktanzahl werden erzeugt, indem zufällige Quadrate oder Hexagone innerhalb der Aggregationsgrenze simuliert werden, anstatt für jede Abschnittsgröße ein vollständiges Mosaik zu konstruieren. Dadurch wird die Verarbeitung beschleunigt, aber die Ergebnisse weichen bei erneuter Ausführung des Werkzeugs etwas ab. Sie können jedoch die Umgebung Zufallszahlengenerator verwenden, um reproduzierbare Ergebnisse sicherzustellen. Die Anzahl der simulierten Polygone für jede Abschnittsgröße wird so berechnet, dass durchschnittlich 75 Prozent der Aggregationsgrenze durch die Simulationen abgedeckt sind.
Bootstrap-Konfidenzintervalle
Die orangefarbenen Konfidenzintervalle um die empfohlene Abschnittsgröße in den Diagrammen herum werden mit Bootstrapping erstellt. Bei diesem Prozess wird ein zufälliges Resampling der Auswertungsergebnisse mit Ersetzung durchgeführt und für jeden Resampling-Satz von Auswertungsergebnissen ein Spline geschätzt. Für jedes Resampling wird das Auswertungsergebnis der ursprünglichen empfohlenen Abschnittsgröße aufgezeichnet und das fünfte Perzentil ermittelt. Abschnittsgrößen, deren Auswertungsergebnis über diesem Wert liegt, werden in das Konfidenzintervall einbezogen. Diese Abschnittsgrößen können so interpretiert werden, dass ihre Auswertungsergebnisse nicht wesentlich niedriger sind als das Auswertungsergebnis der vom Werkzeug empfohlenen Abschnittsgröße.
H3-Hexagone
Das Werkzeug lässt keine Aggregation in H3-Hexagone zu. Sie können jedoch bei der Aggregation in Hexagone die zugehörigen H3-Auflösungen als Führungslinien im Diagramm Auswertungsergebnisse in allen Abschnittsgrößen anzeigen. Die Führungslinien sind standardmäßig deaktiviert, Sie können sie jedoch auf der Registerkarte Führungslinien im Bereich Diagrammeigenschaften aktivieren.

Wen die Führungslinien (gestrichelte graue vertikale Linien) aktiviert sind, können Sie die Auswertungsergebnisse der H3-Auflösungen sehen, die im Bereich der getesteten Abschnittsgrößen liegen, und die für die Daten am besten geeignete Auflösung auswählen. In der folgenden Abbildung hat H3-Auflösung 4 das höchste Auswertungsergebnis, liegt der empfohlenen Abschnittsgröße am nächsten und befindet sich im Konfidenzintervall.

Referenzen
Bei der Implementierung des Werkzeugs wurden folgende Ressourcen verwendet:
- Ramos, Rafael G. 2025. "Finding an Adequate Areal Unit to Map Crime: A Spatial Data Perspective." New Research in Crime Modeling and Mapping Using Geospatial Technologies (Seite 27-44). Cham: Springer Nature Switzerland. https://doi.org/10.1007/978-3-031-81580-5_2.