How Space Time Kernel Density works

Available with Spatial Analyst license.

The Space Time Kernel Density tool expands kernel density calculations from analyzing the relative position and magnitude of the input features to include other dimensions such as time and depth (elevation). The resulting output identifies the magnitude-per-unit area using the multiple kernel functions to fit a smoothly tapered surface to each input point.

Compare to other density tools

Density analysis is key to a number of spatial analysis and geostatistical analysis. Examples include the following:

• Demographic studies
• Concentration, exposure, and resiliency research
• Policymaking to aid in determining the need for any specific services at any specific location or community, such as health care facilities, emergency services, infrastructure, and road networks

Other tools for calculating density are available, including Kernel Density, Point Density, and Line Density. Those tools calculate the density of features (points or lines) in a neighborhood around features. However, they do not consider other dimensions.

The Space Time Kernel Density tool analyzes the density of events or incidents that occur over both space and time as well as being able to consider elevation. By incorporating elevation and time into the equation, the tool expands the understanding of the spatial and temporal distributions and patterns and trends of the phenomenon under consideration.

Key benefits of Space Time Kernel Density

The Space Time Kernel Density tool combines the concepts of kernel density estimation with temporal analysis to provide a comprehensive understanding of patterns. Some of the benefits this tool offers over other forms of density estimation include the ability to do:

• Analyze both the spatial and temporal dimensions of events simultaneously at different elevations. This provides a more holistic understanding of patterns and helps identify areas with high or low concentrations of events over time, across space and elevation.
• Account for the temporal aspect to analyze how event density changes over time. This is particularly useful for studying dynamic phenomena, such as crime patterns, disease outbreaks, or transportation flows.
• Consider both the elevation and temporal aspect together, allowing you to analyze how event density changes over time at different elevation. This is particularly useful for studying dynamic phenomena in geosciences—such as air pressure, ozone density, pollutants, air and water composition, water salinity, dissolved oxygen level, water conductivity, water pressure, and temperature.
• Provide flexibility in parameter selection, including the choice of kernel type, search radius (bandwidth), elevation, and time unit. This allows you to tailor the analysis to specific needs and data characteristics, resulting in more accurate and meaningful results.
• Leverage the existing capabilities of ArcGIS Pro to analyze and visualize Multidimensional raster data and provide various visualization options with the Esri Cloud Raster Format (CRF) format for multidimensional data as the default output raster. This is particularly beneficial to isolate any specific dimension or to visualize and help in identifying hotspots, trends, and patterns within the data across space and time, enabling better decision-making and understanding of spatial-temporal relationships.

This tool offers a more nuanced understanding of event patterns. It can be applied in various fields, including crime analysis, disease mapping, transportation planning, environmental monitoring, oceanographic, and atmospheric sciences. Its ability to analyze both space and time makes it a versatile tool for understanding complex phenomena. However, its specific benefits and suitability may vary depending on the nature of the data and analysis objectives.

How Space Time Kernel Density is calculated

The Space Time Kernel Density tool uses point features with elevation and time data to calculate the kernel density of point features around each output raster cell.

Conceptually, a smoothly curved surface is fitted over each point. The technique is similar to how the Kernel Density tool works for point input. The surface value at the location of the point is the highest and continue to decrease with increasing distance from the point location, reaching zero at the value of the Search Radius parameter distance from the point. Since the input data type is point, only a circular neighborhood is possible. The volume under the surface equals the Population Field parameter's value for the point, or 1 if NONE is specified. The density at each output raster cell is calculated by adding the values of all the kernel surfaces where they overlay the raster cell center. The kernel function is based on the quartic kernel function described in Silverman (1986, p. 76, equation 4.5).

The formula is as follows:

Where:

• i = 1,…,n are the input points.
• f(j) is the density at the center of each cell.
• d_ij is the distance between the incident point and the center of the cell.
• h is the search radius.

If a Population Field parameter setting other than NONE is used, each item's value determines the number of times to count the point. For example, a value of 3 will cause the point to be counted as three points. The values can be integer or floating point.

By default, a unit is selected based on the linear unit of the projection definition of the input point feature data or as otherwise specified in the Output Coordinate System environment setting.

If an output Area units parameter factor is selected, the calculated density for the cell is multiplied by the appropriate factor before it is written to the output raster. For example, if the input units are meters, the output area units will default to Square Kilometers. The end result of comparing a unit scale factor of meters to kilometers will result in the values being different by a multiplier of 1,000,000 (1,000 meters × 1,000 meters).

Predict the density for a location

The predicted density at a new (x,y) location is determined by the following formula:

Where:

• i = 1,…,n are the input points. For dist_i < radius, only include points in the sum if they are within the radius distance of the (x,y) location.
• pop_i is the population field value of point i. This is an optional parameter.
• dist_i is the distance between point i and the (x,y) location.
• radius is the defined search radius around the (x,y) location.

The calculated density is then multiplied by the number of points or the sum of the population field if one was provided. This correction makes the spatial integral equal to the number of points (or sum or population field) rather than always being equal to 1. This implementation uses a Quartic kernel as described in Silverman (1986). The formula will be calculated for every location where you want to estimate the density. Since a raster is being created, the calculations are applied to the center of every cell in the output raster.

Time and elevation

Density can be calculated across time, across elevation, or across both time and elevation. Use the time dimension to analyze patterns and trends over time within a defined time range. Use the elevation dimension to account for the influence of topography on the distribution of events.

The following sections provide more information about the parameters for these dimensions and the formulas that are used.

Kernel density across time over (x,y) points

To include the time dimension in the calculation of this tool, you need to establish the start time, the end time, and the time interval.

The Start Time parameter specifies the beginning of the time period over which you want to calculate the density. It can be a specific date (such as, 12/31/2023), or time (3:45:45 PM), or date and time together (12/31/2023 3:45:45 PM). The start time sets the lower bound of the search time window (t_window) for the calculation.

The End Time parameter specifies the end of the time period for the density calculation. Similar to the start time, it can be a specific date and time or a date and time together. The end time sets the upper bound of the search time window (t_window) for the calculation.

The Time Interval parameter specifies the granularity of the time intervals used in the analysis. It specifies the length of each time interval, such as 1 hour, 1 day, or 1 month. The time interval divides the time range between the start and end times into smaller segments for density calculation. The interval unit could be second, minute, hour, day, or week.

Based on the specified start time, end time, and time interval, the tool calculates the density of events within each time interval and across the specified time range. By dividing the time range between the start time and end time into smaller segments based on the specified time interval, the tool calculates the density of events within each time interval. This allows for a more detailed analysis of how event density varies over time. For example, if the time interval is set to 1 hour and the time range is from 9:00 AM to 5:00 PM, the tool will calculate the density of events within each hour (9:00-10:00 AM, 10:00-11:00 AM, and so on) to provide insights into the temporal patterns of event occurrence.

For calculating the kernel density across time over (x,y) points, a spatial kernel, k(x,y), and a temporal kernel, k(t) are used. This results in the following formula for kernel density across time:

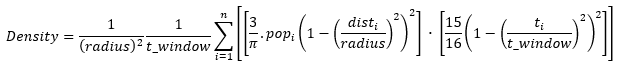
Where:

• For dist_i < radius, only include points in the sum if they are within the radius distance of the (x,y) location.
• For t_i < t_window, only include time in the calculation if they are within the time window defined with the start and end time.
• pop_i is the population field value of point i. This is an optional parameter.
• dist_i is the distance between point i and the (x,y) location.
• radius is the defined search radius around the (x,y) location.
• t_i is the time at each interval calculated within the time window (t_window).
• t_window is the time window defined with the start and end time.

Kernel density across different elevation over (x,y)

The elevation parameters are used to analyze the density of events or phenomena that occur over both space and elevation. The tool accounts for the spatial location of events as well as the elevation at which they occur. To calculate the elevation dimension in this tool, you need to specify three parameters: minimum elevation, maximum elevation, and elevation interval.

The Minimum Elevation parameter specifies the lowest elevation value within the range of elevations you want to consider for the density calculation. It sets the lower bound of the elevation range for the analysis.

The Maximum Elevation parameter specifies the highest elevation value within the range of elevations you want to consider. Similar to the minimum elevation, it sets the upper bound of the elevation range for the analysis.

The Elevation Interval parameter specifies the granularity of the elevation intervals used in the analysis. It specifies the length of each elevation interval, such as 100 meters, 500 meters, or 1 kilometer. The elevation interval divides the elevation range between the minimum and maximum elevations into smaller segments for density calculation.

By specifying the minimum elevation, maximum elevation, and elevation interval, the tool calculates the density of events within each elevation interval and across the specified elevation range.

For calculating the kernel density across elevation over (x,y) points, a spatial kernel, k(x,y), and an elevation kernel, k(z) are used. This results in the following formula for kernel density across time:

Where:

• For dist_i < radius, only include points in the sum if they are within the radius distance of the (x,y) location.
• For z_i < z_distance, only include elevation points in the calculation if they are within the elevation window defined with the minimum and maximum elevation.
• pop_i is the population field value of point i. This is an optional parameter.
• dist_i is the distance between point i and the (x,y) location.
• radius is the defined search radius around the (x,y) location.
• z_i is the elevation at each interval calculated within the elevation window.
• z_distance is the elevation window defined with the minimum and maximum elevation.

Kernel density across different elevation and time over (x,y)

The kernel density can be analyzed across both elevation and time dimensions. To do so, you need to specify six parameters: minimum elevation, maximum elevation, elevation interval, start time, end time, and time interval.

For calculating the kernel density across different elevation and time over (x,y) points, the following formula is used:

Where:

• For dist_i < radius, only include points in the sum if they are within the radius distance of the (x,y) location.
• For z_i < z_distance, only include elevation points in the calculation if they are within the elevation window defined with the minimum and maximum elevation.
• For t_i < t_window, only include time in the calculation if they are within the time window defined with the start and end time.
• pop_i is the population field value of point i. This is an optional parameter.
• dist_i is the distance between point i and the (x,y) location.
• radius is the defined search radius around the (x,y) location.
• z_i is the elevation at each interval calculated within the elevation window.
• z_distance is the elevation window defined with the minimum and maximum elevation.
• t_i is the time at each interval calculated within the time window (t_window).
• t_window is the time window defined with the start and end time.

Search window parameters

The search radius (or bandwidth as it is referred in the Kernel Density tool) determines the extent or reach of influence that each event has on the density calculation. It plays a crucial role in defining the spatial and temporal scope of the analysis. For more information, see Default search radius (bandwidth) in the Kernel Density tool help.

In the Space Time Kernel Density tool, you can specify the search radius separately for three types of dimensions: (x, y), elevation (z), and time (t).

Search radius for x and y

The Search Radius (x and y) parameter specifies the distance within which events will influence the density calculation in the x and y dimensions. The search radius can be in the same unit as the input data or can be specified in units such as meters, kilometers, or degrees.

Specifying a larger search radius will result in a smoother density surface, as events farther away from a particular location will have a greater influence on its density value.

Search radius for elevation

The Search Radius (z) parameter determines the vertical distance within which events will influence the density calculation in the elevation dimension. It can be specified in units such as meters, feet, or it can be the same as the elevation units of the input data.

Similar to the x and y search radius, specifying a larger elevation search radius will result in a smoother density surface, as events at greater vertical distances from a particular location will have a greater influence on its density value.

Search radius for time

The Search Time Window (t) parameter defines the temporal extent within which events will influence the density calculation. It can be specified in units such as hours, days, or months. The time window sets a duration around each event, and events occurring within this duration will contribute to the density calculation at a specific location and time.

Detail and smoothness of the result

By adjusting the search radius values under the Kernel parameters tab, you can control the level of detail and smoothness in the resulting density surface. A smaller search radius or bandwidth will capture more localized patterns, while a larger search radius or bandwidth will capture broader trends and patterns.

Selecting an appropriate search radius or bandwidth values requires careful consideration of the characteristics of the data and the analysis objectives. Experimenting with different values and evaluating the resulting density surfaces can help find the most suitable parameters for your specific analysis.

Search radius calculation

The algorithm used to determine the default search radius does the following:

• Calculate the mean center of the input points. If a population field was provided, this, and all the following calculations, will be weighted by the values in that field.
• Calculate the distance from the weighted mean centers for all points.
• Calculate the weighted median of these distances, D_m.
• Calculate the weighted Standard Distance, SD.

Note:

See How Standard Distance works in the Spatial Statistics toolbox help for details about how standard distance is calculated.

The default search radius for (x,y) is determined by the following formula:

Where:

• SD is the standard distance.
• D_m is the (weighted) median distance from (weighted) mean center.
• n is the numbers of points if no Population Field parameter value is specified. If the Population Field parameter value is provided, n is the sum of the field values.

The default search radius for elevation (z_distance) and time window (t_window) is determined by the following formula:

Where:

• σ_z,t is the standard deviation in the point distribution of the z and t dimensions.
• n is the numbers of points if no Population Field parameter value is specified. If the Population Field parameter value is supplied, n is the sum of the field values.
• d is the analysis dimension. The default value is 1.

Standard distance calculation

There are two methods for calculating the standard distance, unweighted and weighted.

The unweighted distance is determined by the following formula:

Where:

• x_i,y_i, and z_i are the coordinates for featurei.
• {x̄, ȳ, z̄} represents the mean center for the features.
• n is equal to the total number of features.

The weighted distance is determined by the following formula:

Where:

• w_i is the weight at feature i .
• x_i, y_i, and z_i are the coordinates for featurei.
• {X̄_w, Ȳ_w, Z̄_w} represents the weighted mean center for the features.

Multidimensional raster elevation and time interval

The output from the Space Time Kernel Density tool is a multidimensional raster with individual slices for each elevation and time interval. The total number of slices in the output raster is calculated using the following formula if both elevation and time input data is provided:

Where:

• Z_max is the maximum elevation.
• Z_min is the minimum elevation.
• elevation interval is the interval between elevation slices in the multidimensional raster output.
• T_max is the end time.
• T_min is the start time.
• time interval is the interval between time slices in the multidimensional raster output.

If no interval is defined for time or elevation in the Output Parameters group, the default number of slices will be 20 for operations with any one of the input variables. For operations with both elevation and time, the default number of slices in the output raster is 400.

Effect of planar and geodesic methods on density

The calculation of density will vary depending on the selection of planar or geodesic spatial reference system.

The Planar option of the Method parameter is appropriate if the analysis is to be performed at a local scale with a projection that accurately maintains the correct distance and area. By default, the tool uses planar distance.

The Geodesic option is appropriate if the analysis is to be performed at a regional or large scale, such as when a Web Mercator or any geographic coordinate system is used. This method accounts for the curvature of the spheroid and correctly handles data near the poles and the international dateline. The geodesic method always produces a more accurate result and is the recommended method.

The difference between planar and geodesic distance increases proportionally with distance from the source. If you are working in a small geographical area, such as a city or county, the difference between planar and geodesic is proportionally smaller than if you are working at the scale of an entire country. The impact of size of study area and distortions of the map project can work together to further increase distortion. For a projection such as Web Mercator, the closer toward the poles you go, the smaller area you can analyze with the same amount of distance distortion.

To understand the differences between geodesic and planar distance in distance calculation, see Geodesic versus planar distance.

Output density types

The Resultant Values parameter provides two options with which to calculate and visualize the output density types: Densities and Expected Counts.

If the Densities setting is chosen, the cell values in the output raster represent the calculated density value per unit area.

If the Expected Counts setting is chosen, the values represent the expected number of events per cell area. The formulas used to calculate the counts are as follows:

• With just the radius on the x,y plane, Count = Density × Area.
• With elevation, Count = Density × Area × Elevation interval.
• With time, Count = Density × Area × Time interval.
• With both time and elevation, Count = Density × Area × Elevation interval × Time interval.

It is important to highlight that these formulas assume a constant density within output raster cells, elevation interval, and time interval. In order to generate reliable expected counts, careful consideration should be given to the selection of cell size, elevation interval, and time interval parameter values.

Potential applications

Potential applications for this tool include the following:

• Understand the ocean surface and water composition using both the elevation and time. For example, examine the change in parameters such as salinity, water temperature, or dissolved oxygen level across the ocean over time.
• Understand atmospheric conditions. For example, examine the density changes of PM_2.5 readings over a geographic unit at different times of the day or year.
• Apply the tool's capacity to use time to understand disease outbreak, crime density, or homeless population over different periods of time.
• Analyze the composition of suspended air particles in the atmosphere across different locations and elevations. For example, examine the changes in PM_2.5 composition over time to gain insights into air pollution patterns and identify potential sources of pollution.

Additional resources

Härdle, W. K., Müller, M, Sperlich, S., and Werwatz, A. Nonparametric and semiparametric models (Vol. 1). Berlin: Springer, 2004.

Hu, Y., Wang, F., Guin, C., and Zhu, H. "A spatio-temporal kernel density estimation framework for predictive crime hotspot mapping and evaluation." Applied geography, 99, 2018, 89-97.

Nakaya, T., and Yano, K. "Visualising crime clusters in a space‐time cube: An exploratory data analysis approach using space time kernel density estimation and scan statistics." Transactions in GIS, 14(3), 2010, 223-239.

Silverman, B. W. Density Estimation for Statistics and Data Analysis. New York: Chapman and Hall, 1986.