| Label | Explanation | Data Type |
Input Feature Class | The feature class for which spatial autocorrelation will be calculated. | Feature Layer |
Input Field | The numeric field that will be used in assessing spatial autocorrelation. | Field |
Generate Report (Optional) | Specifies whether a graphical summary of result will be created as an .html file.
| Boolean |
Conceptualization of Spatial Relationships | Specifies how spatial relationships among features will be defined.
| String |
Distance Method | Specifies how distances will be calculated from each feature to neighboring features.
| String |
Standardization | Specifies whether standardization of spatial weights will be applied. Row standardization is recommended whenever the distribution of features is potentially biased due to sampling design or an imposed aggregation scheme.
| String |
Distance Band or Threshold Distance (Optional) | The cutoff distance for the various inverse distance and fixed distance options. Features outside the specified cutoff for a target feature are ignored in analyses for that feature. However, for Zone of indifference, the influence of features outside the given distance is reduced with distance, while those within the distance threshold are equally considered. The distance value provided should match that of the output coordinate system. For the inverse distance conceptualizations of spatial relationships, a value of 0 indicates that no threshold distance is applied; when this parameter is left blank, a default threshold value is computed and applied. This default value is the Euclidean distance, which ensures that every feature has at least one neighbor. This parameter has no effect when polygon contiguity (Contiguity edges only or Contiguity edges corners) or Get spatial weights from file spatial conceptualization is specified. | Double |
Weights Matrix File (Optional) | The path to a file containing weights that define spatial, and potentially temporal, relationships among features. | File |
Number of Neighbors
(Optional) | An integer specifying the number of neighbors that will be included in the analysis. | Long |
Summary
Measures spatial autocorrelation based on feature locations and attribute values using the Global Moran's I statistic.
Learn more about how Spatial Autocorrelation (Global Moran's I) works
Illustration
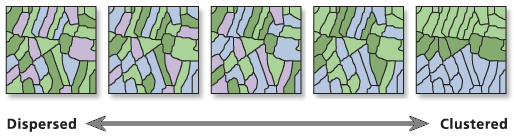
Usage
The Spatial Autocorrelation tool returns five values: the Moran's I Index, Expected Index, Variance, z-score, and p-value. These values are written as messages at the bottom of the Geoprocessing pane during tool operation and are passed as derived output values for potential use in models or scripts. To access the messages, hover over the progress bar and click the pop-out button, or expand the details section of the messages in the Geoprocessing pane. You can also access the messages and details of a previously run tool through the geoprocessing history. You can create an HTML report file with a graphical summary of results using this tool. The path to the report will be included with the messages summarizing the tool parameters. Click this path to open the report file.
For a set of features and an associated attribute, this tool evaluates whether the pattern expressed is clustered, dispersed, or random. When the z-score or p-value indicates statistical significance, a positive Moran's I index value indicates tendency toward clustering, while a negative Moran's I index value indicates tendency toward dispersion.
This tool calculates a z-score and p-value to indicate whether you can reject the null hypotheses. In this case, the null hypothesis states that the values of the features are spatially uncorrelated.
The z-score and p-value are measures of statistical significance. These values can help you determine whether to reject the null hypothesis. For this tool, the null hypothesis states that the values associated with features are randomly distributed.
The Input Field parameter value should contain a variety of values. The math for this statistic requires variation in the variable being analyzed; it cannot solve if all input values are 1, for example. If you want to use this tool to analyze the spatial pattern of incident data, consider aggregating the incident data. You can also use the Optimized Hot Spot Analysis tool to analyze the spatial pattern of incident data.
Note:
Incident data are points that represent events (crime, traffic accidents) or objects (trees, stores) where the focus is on presence or absence rather than a measured attribute associated with each point.
When the Input Feature Class parameter value is not projected (that is, when coordinates are in degrees, minutes, and seconds) or when the Output Coordinate System environment is set to a geographic coordinate system, distances will be computed using chordal measurements. Chordal distance measurements are used because they can be computed quickly and provide good estimates of true geodesic distances, at least for points within approximately 30 degrees of each other. Chordal distances are based on an oblate spheroid. Given any two points on the earth's surface, the chordal distance between them is the length of a line, passing through the three-dimensional earth, to connect the two points. Chordal distances are reported in meters.
Caution:
Ensure that you project the data if the study area extends beyond 30 degrees. Chordal distances are not a good estimate of geodesic distances beyond 30 degrees.
When chordal distances are used in the analysis, the Distance Band or Threshold Distance parameter value, if specified, should be in meters.
For line and polygon features, feature centroids are used in distance computations. For multipoints, polylines, or polygons with multiple parts, the centroid is computed using the weighted mean center of all feature parts. The weighting for point features is 1, for line features is length, and for polygon features is area.
The Conceptualization of Spatial Relationships parameter value should reflect inherent relationships among the features you are analyzing. The more realistically you can model how features interact with each other in space, the more accurate the results will be. Recommendations are outlined in Best practices for selecting a conceptualization of spatial relationships. The following are additional tips:
When using the Fixed distance band option, the default Distance Band or Threshold Distance parameter value will ensure that each feature has at least one neighbor. This is important, but often this default will not be the most appropriate distance to use for an analysis. Additional strategies for selecting an appropriate scale (distance band) for an analysis are outlined in Distance band (sphere of influence).
When using the Inverse distance or Inverse distance squared options, when zero is entered for the Distance Band or Threshold Distance parameter, all features are considered neighbors of all other features; when this parameter is left blank, the default distance will be applied.
Weights for distances less than 1 become unstable when they are inverted. Consequently, the weighting for features separated by less than 1 unit of distance are given a weight of 1.
For the inverse distance options (Inverse distance, Inverse distance squared, and Zone of indifference), any two points that are coincident will be given a weight of 1 to avoid zero division. This assures that features are not excluded from the analysis.
In Python, the derived output of this tool contains the Moran's I index value, z-score, p-value, an HTML report file, and the input features. For example, if you assign the tool's Result object to a variable named MoranResult, MoranResult[0] stores the Moran's I index value, MoranResult[1] stores the z-score, MoranResult[2] stores the p-value, MoranResult[3] stores the file path of the HTML report file, and MoranResult[4] stores the input features. If you do not output an HTML report file using the Generate Report parameter, the fourth derived output will be an empty string.
Additional options for the Conceptualization of Spatial Relationships parameter, including three-dimensional and space-time relationships, are available using the Generate Spatial Weights Matrix tool. To use these additional options, construct a spatial weights matrix file prior to analysis; for the Conceptualization of Spatial Relationships parameter, use the Get spatial weights from file option, and for the Weights Matrix File parameter, specify the path to the spatial weights file you created.
Map layers can be specified as the Input Feature Class parameter value. When using a layer with a selection, only the selected features will be included in the analysis.
If you provide a Weights Matrix File parameter value with a .swm extension, it is expected that a spatial weights matrix file will be created using the Generate Spatial Weights Matrix tool; otherwise, an ASCII-formatted spatial weights matrix file is expected. In some cases, behavior is different depending on the following type of spatial weights matrix file you use:
- ASCII-formatted spatial weights matrix file
- Weights will be used as is. Missing feature-to-feature relationships will be treated as zeros.
- If the weights are row standardized, results may be incorrect for analyses on selection sets. To run an analysis on a selection set, convert the ASCII spatial weights file to a .swm file by reading the ASCII data into a table, and using the Convert table option with the Generate Spatial Weights Matrix tool.
- SWM-formatted spatial weights matrix file
- If the weights are row standardized, they will be restandardized for selection sets; otherwise, weights will be used as is.
- ASCII-formatted spatial weights matrix file
Running an analysis with an ASCII-formatted spatial weights matrix file is memory intensive. For analyses of more than 5,000 features, consider converting the ASCII-formatted spatial weights matrix file to an SWM-formatted file. First, put the ASCII weights into a formatted table (using Excel, for example). Next, run the Generate Spatial Weights Matrix tool using Convert table for the Conceptualization of Spatial Relationships parameter value. The output will be an SWM-formatted spatial weights matrix file.
For polygon features, use the Row option for the Standardization parameter. Row standardization mitigates bias when the number of neighbors of each feature is a function of the aggregation scheme or sampling process, rather than a reflection of the actual spatial distribution of the variable you are analyzing.
For additional information about this tool's parameters, see the Modeling spatial relationships help topic.
Note:
It is possible to run out of memory when you run this tool. This can occur when the specified Conceptualization of Spatial Relationships and Distance Band or Threshold Distance parameter values result in features having thousands of neighbors. As a general rule, do not define spatial relationships so that features have thousands of neighbors. All features should have at least one neighbor and almost all features should have at least eight neighbors.
Caution:
Shapefiles cannot store null values. Tools or other procedures that create shapefiles from other types of inputs may store or interpret null values as zero. In some cases, null values are stored as large negative values in shapefiles, which can lead to unexpected results. See Geoprocessing considerations for shapefile output for more information.
Parameters
arcpy.stats.SpatialAutocorrelation(Input_Feature_Class, Input_Field, {Generate_Report}, Conceptualization_of_Spatial_Relationships, Distance_Method, Standardization, {Distance_Band_or_Threshold_Distance}, {Weights_Matrix_File}, {number_of_neighbors})| Name | Explanation | Data Type |
Input_Feature_Class | The feature class for which spatial autocorrelation will be calculated. | Feature Layer |
Input_Field | The numeric field that will be used in assessing spatial autocorrelation. | Field |
Generate_Report (Optional) | Specifies whether a graphical summary of result will be created as an .html file.
| Boolean |
Conceptualization_of_Spatial_Relationships | Specifies how spatial relationships among features will be defined.
| String |
Distance_Method | Specifies how distances will be calculated from each feature to neighboring features.
| String |
Standardization | Specifies whether standardization of spatial weights will be applied. Row standardization is recommended whenever the distribution of features is potentially biased due to sampling design or an imposed aggregation scheme.
| String |
Distance_Band_or_Threshold_Distance (Optional) | The cutoff distance for the various inverse distance and fixed distance options. Features outside the specified cutoff for a target feature are ignored in analyses for that feature. However, for ZONE_OF_INDIFFERENCE, the influence of features outside the given distance is reduced with distance, while those within the distance threshold are equally considered. The distance value provided should match that of the output coordinate system. For the inverse distance conceptualizations of spatial relationships, a value of 0 indicates that no threshold distance is applied; when this parameter is left blank, a default threshold value is computed and applied. The default value is the Euclidean distance, which ensures that every feature has at least one neighbor. This parameter has no effect when polygon contiguity (CONTIGUITY_EDGES_ONLY or CONTIGUITY_EDGES_CORNERS) or GET_SPATIAL_WEIGHTS_FROM_FILE spatial conceptualization is specified. | Double |
Weights_Matrix_File (Optional) | The path to a file containing weights that define spatial, and potentially temporal, relationships among features. | File |
number_of_neighbors (Optional) | An integer specifying the number of neighbors that will be included in the analysis. | Long |
Derived Output
| Name | Explanation | Data Type |
| Index | The Moran's index value. | Double |
| ZScore | The z-score. | Double |
| PValue | The p-value. | Double |
| Report_File | An HTML file with a graphical summary of results. | File |
| Derived_Input_Dataset | The input features of the tool. | Feature Layer |
Code sample
The following Python window script demonstrates how to use the SpatialAutocorrelation function.
import arcpy
arcpy.env.workspace = r"c:\data"
arcpy.stats.SpatialAutocorrelation("olsResults.shp", "Residual", "NO_REPORT",
"GET_SPATIAL_WEIGHTS_FROM_FILE", "EUCLIDEAN DISTANCE",
"NONE", "#", "euclidean6Neighs.swm")The following stand-alone Python script demonstrates how to use the SpatialAutocorrelation function.
# Analyze the growth of regional per capita incomes in U.S.
# Counties from 1969 -- 2002 using Ordinary Least Squares Regression
# Import system modules
import arcpy
# Set property to overwrite existing outputs
arcpy.env.overwriteOutput = True
# Local variables...
workspace = r"C:\Data"
try:
# Set the current workspace (to avoid having to specify the full path to the feature classes each time)
arcpy.env.workspace = workspace
# Growth as a function of {log of starting income, dummy for South
# counties, interaction term for South counties, population density}
# Process: Ordinary Least Squares...
ols = arcpy.stats.OrdinaryLeastSquares("USCounties.shp", "MYID",
"olsResults.shp", "GROWTH",
"LOGPCR69;SOUTH;LPCR_SOUTH;PopDen69",
"olsCoefTab.dbf",
"olsDiagTab.dbf")
# Create Spatial Weights Matrix (can be based on input or output FC)
# Process: Generate Spatial Weights Matrix...
swm = arcpy.stats.GenerateSpatialWeightsMatrix("USCounties.shp", "MYID",
"euclidean6Neighs.swm",
"K_NEAREST_NEIGHBORS",
"#", "#", "#", 6)
# Calculate Moran's I Index of Spatial Autocorrelation for
# OLS Residuals using a SWM File.
# Process: Spatial Autocorrelation (Morans I)...
moransI = arcpy.stats.SpatialAutocorrelation("olsResults.shp", "Residual",
"NO_REPORT", "GET_SPATIAL_WEIGHTS_FROM_FILE",
"EUCLIDEAN_DISTANCE", "NONE", "#",
"euclidean6Neighs.swm")
except:
# If an error occurred when running the tool, print the error message.
print(arcpy.GetMessages())Environments
Special cases
- Output Coordinate System
Feature geometry is projected to the Output Coordinate System prior to analysis. All mathematical computations are based on the Output Coordinate System spatial reference. When the Output Coordinate System is based on degrees, minutes, and seconds, geodesic distances are estimated using chordal distances.
Licensing information
- Basic: Yes
- Standard: Yes
- Advanced: Yes
Related topics
- An overview of the Analyzing Patterns toolset
- Modeling spatial relationships
- What is a z-score? What is a p-value?
- Find a geoprocessing tool
- Average Nearest Neighbor
- Cluster and Outlier Analysis (Anselin Local Moran's I)
- Hot Spot Analysis (Getis-Ord Gi*)
- Spatial weights
- How Spatial Autocorrelation (Global Moran's I) works