Available with Geostatistical Analyst license.
Introduction
Empirical Bayesian Kriging 3D (EBK3D) is a geostatistical interpolation method that uses Empirical Bayesian Kriging (EBK) methodology to interpolate points in 3D. All input points must have x- and y-coordinates, an elevation, and a measured value to be interpolated. EBK3D is available in the Geostatistical Wizard and as a geoprocessing tool.
3D interpolation has the following potential applications:
- Oceanographers can create maps of dissolved oxygen and salinity at various depths in the ocean.
- Atmospheric scientists can create models for pollution and greenhouse gasses throughout the atmosphere.
- Geologists can predict subsurface geologic properties such as mineral concentrations and porosity.
The result of the interpolation is a geostatistical layer that shows a horizontal transect at a given elevation. The current elevation can be changed with the Range slider, and the layer will update to show the interpolated predictions for the new elevation. You can export rasters and feature contours at any elevation as well as predict to target points in 3D.
Learn more about the visualization and export options for geostatistical layers in 3D
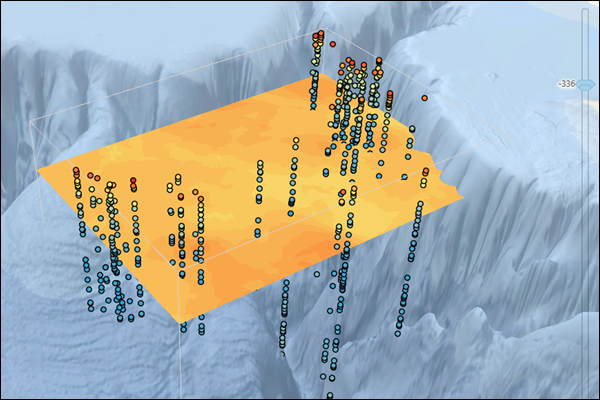
Comparing 2D and 3D Empirical Bayesian Kriging
You are encouraged to read What is Empirical Bayesian Kriging? to understand many of the concepts and mechanics behind EBK3D. The process of subsetting, semivariogram simulation, mixing models, and prediction is identical, with the following exceptions:
- All distances, including those used to estimate the semivariogram, are calculated using 3D Euclidean distance.
- Subsets are constructed in 3D.
- Neighbors for prediction are found using 3D search neighborhoods.
The same subsetting options, semivariogram models, and transformations are available in 2D and 3D, and the criteria for choosing them is the same in both dimensions.
Horizontal and vertical change in data values
One of the most challenging properties of data collected in 3D is that the values of the points often change more quickly in the vertical direction than in the horizontal direction. Environmental processes, such as temperature, ocean salinity, pressure, and so on, change relatively slowly, moving along the same elevation. However, they change quickly as the elevation increases or decreases. This means that to make a prediction at a new location, the search neighborhood can search for neighbors farther horizontally than vertically. To account for the difference in how the data values change horizontally and vertically, you can apply an Elevation inflation factor, and you can remove linear trends in the vertical direction.
Elevation inflation factor
The first method for accounting for vertical and horizontal difference is the elevation inflation factor. It is a positive number that is multiplied to the Elevation field value prior to subsetting and model estimation. By multiplying the elevation values by this value, you stretch the elevations of the points vertically while keeping the horizontal coordinates the same. After making predictions in the stretched coordinates, the results are stretched back to the original coordinates before displaying the results in the map.

The goal is to choose an inflation factor where the measured values of the stretched points change at the same rate vertically as horizontally. For example, if the values of some points change on average five times faster vertically than they do horizontally, multiplying the elevation values by five will result in new coordinates where the values of the points change at the same rate horizontally as vertically. Stretching the elevation values in this way allows accurate estimation of the semivariogram, and it allows the search neighborhood to find appropriate neighbors and assign correct weights.
If no elevation inflation factor is provided, a value will be estimated at run time using maximum likelihood estimation, and the value will be printed as a geoprocessing message. The value calculated at run time will be between 1 and 1000. However, you can type values between 0.01 and 1,000,000. If the calculated value is equal to 1 or 1000, you can provide values outside that range and choose a value based on cross validation.
Note:
If the distance unit of the elevation field is different than the unit of the horizontal coordinates, the elevation will be converted to the unit of the horizontal coordinates before calculating the elevation inflation factor. This means that changing the unit of the elevation field will not change the value of the elevation inflation factor.
Vertical trend removal
The Order of trend removal parameter can be used to remove linear trend in the vertical direction. If applied, the model will estimate a first-order coefficient for the z-coordinate. This option is appropriate for data that gets systematically larger or smaller as the elevation increases or decreases. Whereas the elevation inflation factor corrects for rapidly changing values vertically, trend removal corrects for consistent changes in data values as elevation increases or decreases, regardless of how rapidly the values change. If this option is used, the elevation inflation factor should be interpreted in terms of the detrended data values, and it will usually be smaller than it would be if trend removal had not been performed.
3D interpolation in the Geostatistical Wizard
Empirical Bayesian Kriging 3D can be performed in an interactive environment using the Geostatistical Wizard. You are guided through the process of specifying your input points, configuring parameters, and viewing cross validation results. This experience of choosing parameters, viewing the preview surface, and investigating cross validation results is the same as 2D Empirical Bayesian Kriging, and all of the same graphs and options appear in the same places.
You can change the elevation of the preview surface by either dragging the elevation slider on the right of the preview surface or typing a value beneath the slider. This allows you to interactively view horizontal transects at different elevations. This experience is analogous to using the range slider to change the elevation of the geostatistical layer in a map outside of the wizard. You can also change the elevation by typing a value into the Z coordinate on bottom-right section of the preview page.

The Elevation inflation factor will optimize itself by default. If you change any other parameters, such as the semivariogram model or the subset size, you can calculate a new optimal elevation inflation factor using the Optimize button  .
.
Performance considerations
There are several performance considerations when choosing the parameters of this tool. Some of the following options will increase the calculation time of the method, and you may need to choose which advanced options are most critical in order to maintain a manageable calculation time:
- Estimating the Elevation inflation factor parameter takes a significant portion of the calculation time. Manually typing a value will avoid that portion of the calculation.
- Using a transformation or a K-Bessel semivariogram model will increase the number of parameters that need to be estimated, which will increase calculation time.
- The number of neighbors in the search neighborhood affects the calculation time. The minimum and maximum number of neighbors applies to each sector of the neighborhood, so, for example, if you use 20 sectors and at least 5 neighbors per sector, each prediction will use at least 100 neighbors (5 in each of the 20 sectors). It's recommended that you reduce the number of neighbors per sector when using large numbers of sectors. Generally, 10 to 20 neighbors is sufficient for accurate and stable prediction.
References
- Chilès, J-P., and P. Delfiner (1999). Chapter 4 of Geostatistics: Modeling Spatial Uncertainty. New York: John Wiley & Sons, Inc.
- Krivoruchko K. (2012). "Empirical Bayesian Kriging," ArcUser Fall 2012.
- Krivoruchko K. (2012). "Modeling Contamination Using Empirical Bayesian Kriging," ArcUser Fall 2012.
- Krivoruchko K. and Gribov A. (2014). "Pragmatic Bayesian kriging for non-stationary and moderately non-Gaussian data," Mathematics of Planet Earth. Proceedings of the 15th Annual Conference of the International Association for Mathematical Geosciences, Springer 2014, pp. 61-64.
- Krivoruchko K. and Gribov A. (2019). "Evaluation of empirical Bayesian kriging," Spatial Statistics Volume 32. https://doi.org/10.1016/j.spasta.2019.100368.
- Pilz, J., and G. Spöck (2007). "Why Do We Need and How Should We Implement Bayesian Kriging Methods," Stochastic Environmental Research and Risk Assessment 22 (5):621–632.