La herramienta Estadísticas de resumen de vecindad calcula estadísticas de resumen locales de uno o varios campos numéricos de entidades de puntos o poligonales utilizando vecindades. Las estadísticas locales incluyen el valor medio (promedio), la mediana, la desviación estándar, el rango intercuartílico, el sesgo y el desequilibrio de cuantiles. Entre las vecindades están banda de distancia, número de vecinos, contigüidad de polígono y archivos de ponderaciones espaciales. Es posible ponderar geográficamente todas las estadísticas locales utilizando kernels.
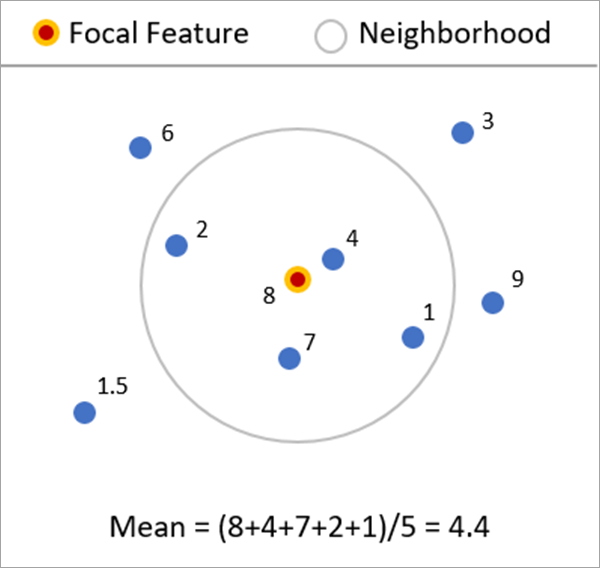
Tipos de vecindad
El parámetro Tipo de vecindad tiene seis opciones que se pueden utilizar para definir las entidades que se utilizan como vecinos de cada entidad focal.
- Banda de distancia: se utilizan como vecinos todas las entidades existentes dentro de una distancia especificada (hasta un máximo de 1.000). Este valor predeterminado es la distancia euclidiana que garantiza que cada entidad tenga como mínimo un vecino.
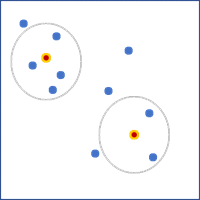
- Número de vecinos: se utiliza como vecinos un número fijo de entidades más cercanas.
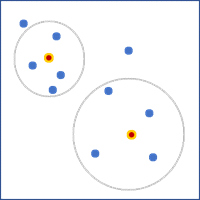
- Solo bordes de contigüidad: se usa como vecino cualquier polígono que comparta un borde con la entidad focal. Esta opción solo es aplicable a las entidades poligonales.
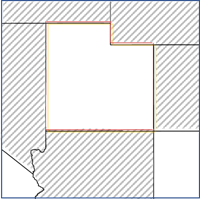
- Bordes o esquinas de contigüidad: se usa como vecino cualquier polígono que comparta un borde o esquina con la entidad focal. Esta opción solo es aplicable a las entidades poligonales.
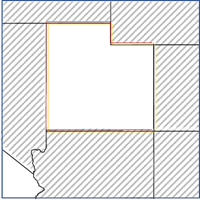
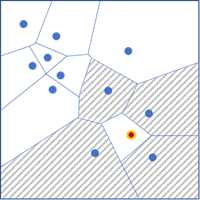
- Triangulación de Delaunay: los vecinos se definen por compartir bordes o esquinas en su triangulación de Delaunay. Utilizar esta opción equivale a utilizar la herramienta Crear polígonos de Thiessen con los puntos y utilizar la opción Bordes o esquinas de contigüidad con los polígonos de Thiessen. Esta opción solo está disponible para las capas de entidades de puntos.
- Obtener ponderaciones espaciales a partir del archivo: los vecinos y las ponderaciones de cada entidad se definen por un archivo de matriz de ponderaciones espaciales especificado en el parámetro Archivo de matriz de ponderaciones. Es posible crear los archivos con las herramientas Generar matriz de ponderaciones espaciales o Generar ponderaciones espaciales de red.
Resumen de estadísticas
Existen seis estadísticas de resumen que se pueden calcular para cada campo de análisis, especificadas con el parámetro Estadística de resumen local. Las seis estadísticas contienen medidas de centralidad, medidas de variabilidad y propagación y medidas de simetría. Cada clase proporciona dos estadísticas: una tradicional y otra robusta. Las estadísticas robustas son medidas estadísticas que no se ven afectadas por un número reducido de valores atípicos.
La opción Todo del parámetro Estadística de resumen local se utiliza de forma predeterminada para calcular las seis estadísticas para cada campo de análisis. Las fórmulas de las distintas estadísticas se pueden ver en la sección Fórmulas de las estadísticas locales.
Se utilizan mediciones de centralidad para estimar el centro o centro de una distribución de valores. Es posible utilizar estas opciones para suavizar los valores en los datos que contengan ruido. Las medidas de centralidad son las siguientes:
- Valor medio (tradicional): la media aritmética (promedio) de los valores del campo de análisis.
- Mediana (robusta): el percentil 50 de los valores del campo de análisis. La mitad de los valores se encuentran por debajo y la mitad por encima de la mediana.
Se utilizan medidas de variabilidad o dispersión para estimar el rango de la distribución de los valores probables. Puede utilizar estas opciones para investigar si la variabilidad en los campos de análisis es similar en el mapa (llamada estacionariedad de varianza) o si ciertas áreas tienen una variabilidad local más alta que otras. Las medidas de variabilidad son las siguientes:
- Desviación estándar (tradicional): la desviación estándar de los valores del campo de análisis.
- Rango entre cuartiles (robusto): el rango de la mitad media de los valores del campo de análisis (el percentil 75 menos el percentil 25). La mitad de los datos están dentro de este rango.
Se utilizan medidas de simetría para medir si la forma de una distribución es simétrica en torno al centro. Estas opciones se pueden utilizar para investigar la frecuencia de los valores extremos altos y bajos. Las medidas de simetría son las siguientes:
- Sesgo (tradicional): el sesgo de los valores del campo de análisis.
- Desequilibrio de cuantiles (robusto): un valor de -1 a 1 que indica la posición de la mediana con respecto a los percentiles 25 y 75. Los valores cercanos a -1 indican que la mediana está cerca del percentil 25 y los valores cercanos a 1 indican que la mediana está cerca del percentil 75. Los valores cercanos a 0 indican simetría si la mediana está a medio camino entre los percentiles 25 y 75.
Salidas de la herramienta
Las entidades de salida se simbolizan en el mapa utilizando la estadística especificada en el parámetro Estadística de resumen local calculada para el primer campo de análisis (o la distancia a vecinos si no se proporcionan campos de análisis). Si elige Todo para la estadística de resumen local, las entidades muestran los resultados de la estadística Valor medio. Las estadísticas de resumen de todos los demás campos de análisis se guardan como campos en las entidades de salida, junto con copias de todos los campos de análisis. También existen campos que indican la cantidad de vecinos utilizados para cada campo de análisis.
Estadísticas de resumen ponderadas geográficamente
Cuando el parámetro Tipo de vecindad se especifica como Banda de distancia o Número de vecinos, todas las estadísticas se pueden ponderar geográficamente mediante el parámetro Esquema de ponderación local. Si especifica Obtener ponderaciones espaciales a partir del archivo para el parámetro Tipo de vecindad, se utilizan como esquema de ponderación las ponderaciones especificadas en el archivo. Si aplica un esquema de ponderación, todas las estadísticas de resumen se ponderan de modo que los vecinos que están más cerca de la entidad focal reciben ponderaciones más altas en los cálculos, mediante una función, denominada kernel, que disminuye con la distancia a la entidad focal. Se proporcionan dos funciones kernel en el parámetro Esquema de ponderación local.
- Bicuadrado
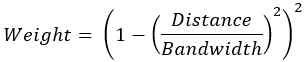
- Gaussiano
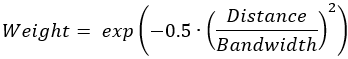
Las funciones de kernel dependen de un ancho de banda que controla la velocidad con la que los pesos disminuyen con la distancia. El ancho de banda de cada kernel se proporciona en el parámetro Ancho de banda kernel. Si no proporciona un valor, se estima un valor predeterminado en tiempo de ejecución y se muestra como un mensaje de geoprocesamiento. Consulte Cómo funciona Densidad kernel para obtener información sobre cómo se calcula este ancho de banda predeterminado.
Nota:
Para la vecindad de banda de distancia, el ancho de banda kernel se establece de forma predeterminada en el mismo valor que el parámetro Banda de distancia.
Fórmulas para las estadísticas locales
Esta sección contiene las fórmulas para las versiones ponderadas y sin ponderar de todas las estadísticas de resumen de una sola entidad focal. Estas fórmulas se aplican a cada entidad de entrada para todos los campos de análisis.
En todas las fórmulas, i = 1, ..., n son los vecinos de la entidad focal (posiblemente incluyendo la entidad focal) ordenada por valor (xi) en orden ascendente. Todos los pesos (wi) se normalizan para sumar uno antes de aplicar estas fórmulas. La versión sin ponderar de cada estadística se deriva estableciendo wi = 1/n para todos los vecinos i.
Estadísticas tradicionales
La siguiente tabla muestra la versión ponderada y sin ponderar de cada estadística de resumen tradicional.
| Estadística | Fórmula ponderada | Fórmula no ponderada |
|---|---|---|
Valor medio | 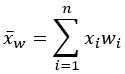 | 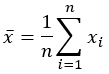 |
Desviación estándar | 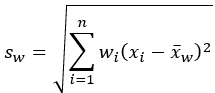 | 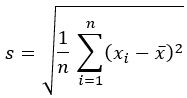 |
Sesgo | 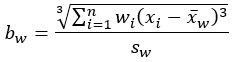 | 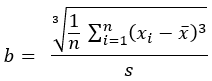 |
Estadísticas robustas
Todas las estadísticas robustas dependen de la definición de un cuantil p ponderado, estando p entre 0 y 1. Esta definición se utiliza para calcular la mediana ponderada (p=0,5), el primer cuartil (p=0,25) y el tercer cuartil (p=0,75). El cuantil p para un p determinado se define como sigue:
- Cuantil p ponderado:
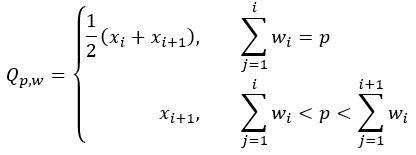
- Cuantil p no ponderado:
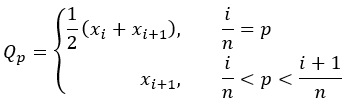
Cuando se utiliza la definición anterior de cuantil p, la siguiente tabla muestra la versión ponderada y no ponderada de cada estadística de resumen robusta.
| Estadística | Fórmula ponderada | Fórmula no ponderada |
|---|---|---|
Mediana | 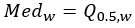 | 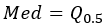 |
Rango intercuartílico | 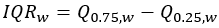 | 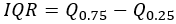 |
Desequilibrio de cuantiles | 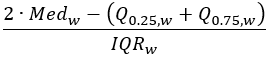 | 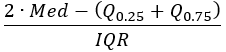 |
Recursos adicionales
Para obtener información adicional sobre las estadísticas de resumen ponderadas geográficamente, consulte la siguiente referencia:
- Brunsdon, C., Fotheringham, A.S., Charlton, M. (2002). "Geographically weighted summary statistics — a framework for localised exploratory data analysis." Computers, Environment and Urban Systems, 26(6): 501-524. ISSN 0198-9715. https://doi.org/10.1016/S0198-9715(01)00009-6.