Disponible con una licencia de Geostatistical Analyst.
En la mayoría de las publicaciones acerca del mundo del SIG, la interpolación de área se entiende específicamente la reagregación de datos de un conjunto de polígonos (los polígonos de origen) a otro conjunto de polígonos (los polígonos de destino). Por ejemplo, es frecuente que los demógrafos tengan que reducir el tamaño o aumentar la escala de las unidades administrativas de sus datos. Si se han tomado recuentos de población a nivel de condado o provincia, el demógrafo podría tener que reducir la escala de los datos para predecir la población de los bloques censales. En el caso de la reorganización de distritos a gran escala, es posible que se necesiten predicciones de población para un conjunto de polígonos completamente nuevo.
La interpolación de área de la extensión ArcGIS Geostatistical Analyst es una técnica de interpolación de estadísticas geográficas que lleva la teoría del kriging a los datos promediados o agregados sobre polígonos. Permite realizar predicciones y errores estándar para todos los puntos incluidos y entre los polígonos de entrada, y las predicciones (junto con errores estándar) se pueden volver a agregar a un nuevo conjunto de polígonos.
Otros métodos de kriging de Geostatistical Analyst requieren datos de puntos continuos y gaussianos, pero la interpolación de área permite que los datos poligonales sean recuentos discretos. También se puede utilizar un segundo conjunto de polígonos como una variable de cokriging; estos polígonos secundarios pueden tener una geometría idéntica a los polígonos de la variable primaria, o los polígonos pueden ser completamente diferentes.
Nota:
Otros métodos de interpolación de Geostatistical Analyst aceptan entradas poligonales, pero asocian el valor del polígono con su centroide y lo tratan como punto. Por lo tanto, no se tienen en cuenta los tamaños de los polígonos, y estos métodos son inadecuados para los datos basados en recuentos.
Flujo de trabajo de reagregación de datos de polígono a polígono
La reagregación de datos poligonales (por ejemplo, la reducción de escala de recuentos de población) es un proceso de dos pasos. Primero, se crea una superficie de predicción suave para los puntos individuales a partir de los polígonos de origen (esta superficie se puede interpretar a menudo como una superficie de densidad o de riesgo); a continuación, la superficie de predicción se reagrega a los polígonos de destino. La creación de la superficie de predicción requiere una variografía interactiva, por lo que se debe realizar en Geostatistical Wizard. La salida de Geostatistical Wizard es una capa de estadísticas geográficas de predicciones o errores estándar de la predicción. Si no se requiere la reagregación a nuevos polígonos, el flujo de trabajo puede terminar aquí.
Una vez que se ha creado una superficie de predicción, la agregación de un conjunto diferente de polígonos se realiza con la herramienta de geoprocesamiento De capa de interpolación de área a polígonos. El siguiente gráfico muestra el flujo de trabajo para predecir las tasas de obesidad de los bloques censales de Los Ángeles a partir de la tasa de obesidad de los distritos escolares de Los Ángeles.

Los detalles matemáticos de la desagregación y la reagregación se pueden encontrar en el documento al que se hace referencia al final de este tema.
¿Qué tipos de datos se pueden utilizar en la interpolación de área?
La interpolación de área acepta como entrada tres tipos de datasets poligonales diferentes. Los tres permiten producir superficies de predicción y de error estándar y se pueden reagregar a polígonos de destino. Las interpretaciones de las superficies de predicción y las predicciones reagregadas son distintas para cada tipo de datos, como se describe a continuación.
Datos de medias (gaussianos)
Para proteger la privacidad o reducir los gastos, las mediciones de punto continuas se promedian en ocasiones sobre regiones de área y los datos de puntos originales se descartan o se tratan como privados. Por ejemplo, es posible generar informes de los niveles medios de contaminación de los condados, pero manteniendo en privado las mediciones de los puntos individuales. Si se desconoce en qué lugares se midió la contaminación, otros métodos de kriging no son adecuados.
La interpolación de área de datos continuos requiere que los datos sean gaussianos y estén promediados sobre polígonos definidos. Dados los polígonos y las mediciones medias, se produce una superficie de predicción (o error estándar) para el valor de la variable gaussiana en todos los puntos del dominio de datos.
Los parámetros de entrada son los siguientes:
- Dataset de entrada: especifica las entidades poligonales.
- Campo de valor: especifica el valor promedio para cada polígono del dataset de origen.
Para la interpolación de área gaussiana, la herramienta de geoprocesamiento De capa de interpolación de área a polígonos predice el valor promedio de la variable gaussiana (con errores estándar de la predicción) para los polígonos de destino. Por ejemplo, dada la temperatura media de todos los condados en un día concreto, se puede predecir la temperatura media de las ciudades pertenecientes a los condados.
Recuentos de índice (binomiales)
Una fuente típica de datos poligonales es aquella en la cual se muestrea aleatoriamente a individuos de la población existente dentro de un polígono, y se recuenta el número de personas que presentan una característica concreta (este proceso se conoce como muestreo binomial). El valor de interés es la proporción de los individuos muestreados que presentan dicha característica.
Dada la cantidad de individuos muestreados y el número de individuos que presentan la característica en cada polígono, la interpolación de área de los recuentos binomiales produce una superficie de predicción de riesgo (o superficie de error estándar) para todos los puntos del dominio de datos. El riesgo de cada punto individual representa la probabilidad de que una muestra individual existente en esa ubicación presente la característica.
Por ejemplo, es posible que una empresa desee preguntar a algunos de sus clientes si están satisfechos con el servicio que ofrece la empresa. En este caso, la característica de interés es que el cliente esté satisfecho con el servicio. Es posible que no se conozcan las ubicaciones exactas de los clientes muestreados; quizá la empresa solo conozca su región geográfica (como la ciudad o el prefijo telefónico). La interpolación de área para recuentos binomiales genera un mapa que muestra las ubicaciones en las que la empresa goza de mayor o menor apoyo. Con esta información, la empresa puede investigar en mayor profundidad por qué los clientes de ciertas ubicaciones están más contentos con su servicio que los clientes de otras ubicaciones.
Para obtener unas predicciones precisas, las muestras se deben tomar aleatoriamente. Todos los miembros de la población de un polígono deben tener la misma probabilidad de ser incluidos en la muestra. Si se introdujera cualquier preferencia hacia individuos concretos, las predicciones arrojarían resultados sesgados.
Los parámetros de entrada son los siguientes:
- Dataset de entrada: especifica las entidades poligonales.
- Campo de recuento: especifica el campo que contiene el número de individuos que comparten una característica específica dentro de cada polígono.
- Campo de población: especifica el campo que contiene el número de personas muestreadas en cada polígono.
Para la interpolación de área binomial, la herramienta de geoprocesamiento De capa de interpolación de área a polígonos predice la proporción de personas que presentan la característica en cuestión dentro de cada polígono especificado. Por ejemplo, si se conoce el número de casos de cáncer de pulmón de cada condado de un estado (junto con la población de riesgo de cada condado), es posible predecir la proporción de individuos que padecen cáncer de pulmón en los códigos postales de los condados. Para obtener una estimación del número de casos de cáncer de pulmón en cada código postal, multiplique la proporción prevista de casos de cáncer de pulmón por la población de cada código postal. Del mismo modo, al multiplicar los errores estándar por la población de cada código postal, se obtiene el error estándar para el número previsto de casos de cáncer de pulmón en cada código postal.
Recuentos de evento (Poisson sobredisperso)
Otra fuente común de datos poligonales es el recuento del número de instancias de un determinado evento dentro de un área definida durante un tiempo especificado. Por ejemplo, los observadores de ballenas recopilan sus datos navegando por áreas definidas del océano y contando el número de ballenas que observan. En este caso, un evento sería el avistamiento de una ballena. Dado que se supone que el número de ballenas observadas es proporcional al tiempo que los observadores de ballenas estuvieron observando, es necesario registrar la cantidad de tiempo que pasaron registrando los avistamientos. En cada expedición, los observadores de ballenas conocen el polígono de observación (el área de observación), el número de eventos presenciados (número de ballenas avistadas) y el tiempo que pasaron observando.
La interpolación de área para recuentos de eventos produce una superficie que predice el riesgo subyacente de presenciar un evento en una ubicación específica. Un riesgo mayor significa que existe una mayor probabilidad de presenciar un evento en esa ubicación. En el caso de que el evento sea encontrar un objeto físico (como pueda ser una ballena), la superficie de predicción puede interpretarse como un mapa de densidad.
En la mayoría de los casos de uso, la hora de observación de cada polígono será la misma. Por ejemplo, las estadísticas de delitos suelen aparecer en forma de recuentos para un solo año para cada polígono. Dado que emplear un tiempo de observación constante es muy común, si no se especifica este tiempo, el software presupone que los recuentos se realizaron en una misma unidad de tiempo para cada polígono. En el caso de un censo completo (en el que se observan todos los eventos, como un recuento total de población), se debe presuponer que el tiempo de observación de cada polígono es el mismo.
En estas observaciones, no es necesario presenciar todos y cada uno de los eventos individuales. Solo es necesario que el número de eventos presenciados por unidad de tiempo sea proporcional a la densidad subyacente de lo que se esté observando. En la práctica, significa que la metodología utilizada para hacer las observaciones debe ser aproximadamente la misma en todos los polígonos. Por ejemplo, si un observador de ballenas de una expedición tiene más habilidad para detectar de ballenas que un observador de otra expedición, las predicciones estarán sesgadas.
Los parámetros de entrada son los siguientes:
- Dataset de entrada: especifica las entidades poligonales.
- Campo de recuento: especifica el campo que contiene el número de eventos presenciados en cada polígono.
- Campo de tiempo: especifica opcionalmente la cantidad de tiempo dedicada al recuento en cada polígono. Si el campo se deja en blanco, el software presupone que todos los recuentos se tomaron en una misma unidad de tiempo.
Para la interpolación de área de Poisson sobredisperso, la herramienta de geoprocesamiento De capa de interpolación de área a polígonos predice la cantidad de recuentos por unidad de tiempo para cada polígono especificado. Por ejemplo, si los observadores de ballenas registraron sus horas de observación, la predicción de un nuevo polígono se interpreta como el número esperado de ballenas que se observarán en ese polígono en una sola hora. Para los datos de población censal, la interpretación es simplemente la población predicha del polígono en el momento del censo.
Crear un modelo válido
Al igual que con todos los métodos de interpolación de estadísticas geográficas, la precisión de sus predicciones en la interpolación de área depende de la precisión de su modelo. Teniendo esto en cuenta, se debe tener mucho cuidado a la hora de crear un modelo válido en Geostatistical Wizard.
Debido a que la interpolación de área de Geostatistical Analyst se implementa mediante un marco de kriging, la variografía interactiva es un paso esencial de la creación del modelo. A menudo, resulta difícil evaluar visualmente la calidad de una curva de covarianza, por lo que se proporcionan intervalos de confianza (las líneas verticales rojas del gráfico que aparece a continuación) para cada covarianza empírica (cruces azules). Si se especifica correctamente el modelo de covarianza, se espera que el 90 por ciento de las covarianzas empíricas caigan dentro de los intervalos de confianza. En el siguiente gráfico, 11 de las 12 covarianzas empíricas caen dentro de los intervalos de confianza y 1 punto se encuentra fuera del intervalo de confianza. Indica que el modelo se ajusta a los datos y se puede confiar en los resultados.

A menudo, la curva de covarianza predeterminada no se ajusta bien a los datos. En este caso, es necesario modificar los parámetros de variografía. El ajuste de una curva de covarianza adecuada suele ser difícil, y la mejor manera de mejorar el ajuste es simplemente la práctica; no obstante, mencionamos a continuación algunas reglas generales que pueden ayudar a ajustar un buen modelo:
- Disminuya el valor Tamaño de intervalo hasta que las covarianzas empíricas ya no sean negativas.
- Si el modelo sigue sin ajustarse, experimente con el parámetro Modelo. K de Bessel y Estable son los modelos más funcionales, pero también tardan más en procesarse.
- Si encuentra una combinación de Tamaño de intervalo y Modelo que casi consiga el ajuste, pruebe a disminuir el valor de Espaciado de lattice. No obstante, recuerde que la reducción del espaciado de lattice conlleva un rápido aumento del tiempo de procesamiento. El parámetro de espaciado de lattice se describe en la sección Nuevos parámetros para la interpolación de área que aparece a continuación.
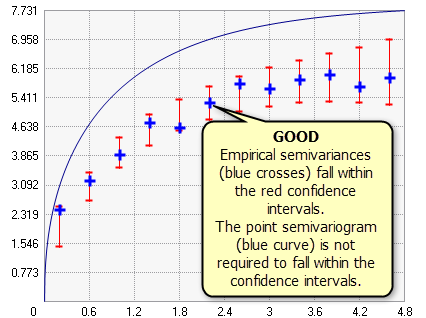
Como se ve en el gráfico siguiente, si Tipo de función se cambia a Semivariograma, la curva de semivariograma de los puntos (la línea azul en el gráfico que aparece a continuación) podría no atravesar los intervalos de confianza. Este hecho no supone un problema en sí mismo, y los criterios para un buen modelo no cambian: si un gran porcentaje de semivarianzas empíricas se encuentra dentro de los intervalos de confianza, puede confiar en la precisión del modelo.
Nuevos parámetros para la interpolación de área
En Geostatistical Wizard, encontrará los tres parámetros siguientes que no aparecen en otros métodos de kriging:
- Espaciado de lattice: para estimar las covarianzas de los puntos, se superpone a cada polígono un lattice cuadrado y se asigna un punto a cada intersección del lattice. El parámetro de espaciado de lattice especifica la distancia horizontal y vertical entre los distintos puntos del lattice. Si el espaciado de lattice es lo suficientemente grande como para que un polígono no reciba ningún punto, se coloca un punto en su centroide. Un espaciado de lattice menor hará predicciones más precisas, pero también aumentará el tiempo de procesamiento. Por ejemplo, si se reduce el espaciado de lattice a la mitad, el procesamiento se cuadruplica.
- Nivel de confianza: especifica el nivel de confianza para los intervalos de confianza de las curvas de semivariograma/covarianza. Si el modelo es correcto, este valor indica el porcentaje de cruces azules (covarianzas/semivarianzas empíricas) que deberían encontrarse dentro de los intervalos de confianza rojos. Tenga en cuenta que la línea de semivariograma de puntos no estará necesariamente dentro de los intervalos de confianza. Este parámetro se usa exclusivamente con fines de diagnóstico; el valor no afectará a las predicciones.
- Parámetro de sobredispersión: solo aplicable a datos de recuento de eventos (Poisson sobredisperso). En los datos de recuento de Poisson, se observa con frecuencia una sobredispersión (mayor variabilidad observada de lo que se espera del modelo). El parámetro de sobredispersión ayuda a corregir este problema. Este parámetro equivale al inverso del parámetro de dispersión de la distribución binomial negativa.
Todos los demás parámetros tienen el mismo significado que en otros métodos de kriging.
Limitaciones
Al igual que con todos los métodos de kriging, la interpolación de área conlleva ciertas limitaciones que pueden impedirle hallar un modelo válido para sus datos.
No estacionariedad
Uno de los supuestos más estrictos del kriging es el supuesto de estacionariedad de los datos. La estacionariedad es el supuesto por el cual la relación estadística entre dos valores de datos de polígono depende únicamente de la distancia entre los polígonos. Por ejemplo, las poblaciones humanas suelen agruparse en ciudades, quedando pocas personas en el espacio que separa a dos ciudades. Este hecho plantea un problema para la interpolación de área debido a que, en virtud de la estacionariedad, la densidad de población debería cambiar sin grandes saltos a lo largo del paisaje; no deberían existir poblaciones extremadamente densas justo al lado de densidades de población tremendamente bajas. En el caso de los datos no estacionarios como estos, el ajuste de un modelo de interpolación de área válido será muy difícil, si no imposible.
Polígonos de tamaños muy diferentes
Si algunos de sus polígonos tienen áreas muy pequeñas en comparación con los polígonos más grandes, es posible que el software no distinga los polígonos más pequeños y los trate como polígonos coincidentes. Podría ocurrir si el parámetro de espaciado de lattice discretiza los polígonos y es posible representar más de un polígono como un único punto en el lattice. Esta situación generará un error porque la interpolación de área no admite el uso de polígonos coincidentes. Para resolver este error, siga estos pasos:
- Utilice las herramientas Buscar idéntico y Eliminar idéntico para localizar y eliminar los polígonos coincidentes. Si no se detecta ningún polígono coincidente o la eliminación no resuelve el error, continúe con el siguiente paso.
- Reduzca manualmente el espaciado de lattice hasta que el software pueda diferenciar los polígonos. Sin embargo, la reducción del espaciado de lattice aumenta rápidamente el tiempo de cálculo. Si descubre que el espaciado de lattice requerido tarda demasiado en procesarse, continúe con el paso siguiente.
- Anule la selección de los polígonos más pequeños de la clase de entidad para que no se utilicen en el cálculo.
Referencias
- Krivoruchko, K., A. Gribov, E. Krause (2011). "Multivariate Areal Interpolation for Continuous and Count Data," Procedia Environmental Sciences, volumen 3: 14–19.