Cuando nos fijamos en el mundo que nos rodea, es muy natural que organicemos, agrupemos, diferenciemos y cataloguemos lo que vemos para ayudarnos a tener un mejor sentido al respecto; este tipo de proceso de clasificación mental es fundamental para el aprendizaje y la comprensión. Del mismo modo, para ayudarle a aprender y comprender mejor los datos, puede utilizar la herramienta Clustering multivariante. Dado el número de clústeres a crear, buscará una solución en la que todas las entidades dentro de cada clúster son lo más parecido posible, y todos los clúster en sí son tan diferentes como sea posible. La similitud de las entidades se basa en el conjunto de atributos que especifica para el parámetro Campos de análisis, y los clústeres se crean mediante el algoritmo de valor medio K.
Sugerencia:
El clustering, el agrupamiento y la clasificación son algunas de las técnicas más utilizadas en aprendizaje de máquina. El Clustering multivariante utiliza métodos no supervisados de aprendizaje de máquina para determinar los clústeres naturales presentes en sus datos. Estos métodos de clasificación se consideran no supervisados porque no requieren un conjunto de entidades previamente clasificadas para guiar o entrenar el método empleado para encontrar los clústeres en sus datos.
A pesar de que existen cientos de algoritmos de análisis de clustering, todos ellos están clasificados como NP-duro. Esto significa que la única forma de garantizar que una solución maximizará perfectamente tanto las similitudes dentro del grupo como las diferencias entre grupos es tratar cada combinación posible de las entidades que desee distribuir en clústeres. Aunque esto puede ser viable con unas cuantas entidades, el problema rápidamente se convierte en incorregible.
No solo es incorregible para garantizar que ha encontrado una solución óptima, sino también es poco realista intentar identificar un algoritmo de clustering que funcionará mejor para todos los tipos de datos y escenarios posibles. Los clústeres son de diferentes formas, tamaños y densidades; los datos de atributos pueden incluir una variedad de rangos, simetría, continuidad y unidades de medición. Esto explica por qué tantos algoritmos de análisis cluster diferentes han sido desarrollados durante los últimos 50 años. Es más adecuado, por lo tanto, pensar en estas herramientas como herramientas de exploración que pueden ayudarle a obtener más información sobre estructuras subyacentes en los datos.
Potenciales aplicaciones
Estas son algunas formas en que se podría aplicar esta herramienta:
- Supongamos que tiene muestras de salmonela de granjas alrededor de su estado y atributos que incluyen el tipo/clase, ubicación y fecha/tiempo. Para comprender mejor cómo las bacterias se transmiten y propagan, puede utilizar la herramienta Clustering multivariante para dividir las muestras en "brotes" individuales. Aunque el análisis en sí no es espacial, podría descubrir un patrón espacial en sus resultados, a medida que el brote se propaga. Una vez que se determinan los clústeres, puede utilizar otras herramientas de análisis de patrón espacial como Elipse de desviación estándar, Centro medio o Cercano para analizar cada brote.
- Si ha recopilado datos sobre avistamientos de animales para entender mejor sus territorios, la herramienta Clustering multivariante podría ser útil. Entender dónde y cuándo se congrega el salmón en diferentes fases de la vida, por ejemplo, podría ayudar a diseñar las áreas protegidas que pueden ayudar a garantizar una reproducción exitosa.
- El clustering de los clientes por sus patrones de compra, características demográficas, patrones de viaje u otros atributos de comportamiento puede ayudarle a diseñar una estrategia de marketing eficiente para los productos de la empresa.
Entradas
Esta herramienta toma Entidades de entrada de punto, polilínea o polígono, una ruta para las Entidades de salida, uno o varios Campos de análisis y un valor entero que representa el Número de clústeres que se desea crear. También existen distintos parámetros opcionales, incluidas opciones para Método de inicialización y una Tabla de salida para evaluar el número óptimo de clústeres.
Campos de análisis
Seleccione los campos que son numéricos y que reflejan relación, intervalo o sistemas de medición ordinales. A pesar de que los datos Nominales se pueden representar mediante variables simuladas (binarias), estos por lo general no funcionan tan bien como los demás tipos de variables numéricas. Por ejemplo, podría crear una variable llamada Rural y asignar a cada entidad (cada distrito censal, por ejemplo) un 1 si es principalmente rural y un 0 si es principalmente urbana. Sin embargo, una mejor representación de esta variable sería la cantidad o la proporción de extensión rural asociada con cada entidad.
Nota:
Los valores de los Campos de análisis están estandarizados en la herramienta porque las variables que tienen grandes variaciones (donde los valores de los datos están muy dispersos alrededor del valor medio) tienden a influir más en los clústeres que las variables que tienen pequeñas variaciones. La estandarización de los valores de atributos implica una transformación z en la que el valor medio de todos los valores se resta de cada valor y se divide entre la desviación estándar de todos los valores. La estandarización pone todos los atributos en la misma escala aunque estén representados por tipos de números muy diferentes: tasas (número de 0 a 1,0), población (valores superior a 1 millón) y distancias (kilómetros, por ejemplo).
Debe seleccionar las variables que considere que distinguirán un clúster de entidades de otro. Supongamos, por ejemplo, que está interesado en realizar un clustering distritos escolares por rendimiento de los estudiantes sobre pruebas estandarizadas de logros. Podría seleccionar Campos de análisis que incluyan los resultados generales de las pruebas, los resultados de temas específicos como matemáticas o lectura, la proporción de los estudiantes que cumplen con un umbral de puntuación mínima en las pruebas, y así sucesivamente. Cuando ejecuta la herramienta Clustering multivariante, se calcula un valor R2 para cada variable, que se comunica en la ventana de mensajes. En el siguiente resumen, por ejemplo, los distritos escolares se agrupan con base en las puntuaciones de las pruebas de los estudiantes, el porcentaje de los adultos en el área que no terminaron la escuela secundaria, por gasto por estudiante y la relación promedio entre estudiantes-profesores. Observe que la variable TestScores tiene el valor R2 más alto. Esto indica que esta variable divide los distritos escolares en clústeres de forma más eficaz. El valor R2 refleja cuánto de la variación en los datos originales de TestScores se mantuvo después del proceso de clustering, de modo que mientras más alto sea el valor R2 para una variable específica, mejor es esa variable en la discriminación entre las entidades.

Explorar:
R2 se calcula como:
(TSS-ESS)/TSS
donde TSS es la suma total de cuadrados y EES es la suma explicada de los cuadrados. TSS se calcula al elevar al cuadrado y luego sumar las desviaciones del valor medio global de una variable. ESS se calcula de la misma manera, excepto que las desviaciones se clasifican por clúster: cada valor se resta del valor medio para el clúster al que pertenece, luego se eleva al cuadrado y se suma.
Número de clústeres
A veces sabrá cuál es el número de clústeres más adecuado para su pregunta o problema, e introduciría ese número en el parámetro Número de clústeres. En muchos casos, sin embargo, usted no tendrá ningún criterio para seleccionar una cantidad específica de clústeres; en lugar de ello, solo desea el número que mejor distingue las similitudes y diferencias de las entidades. Para ayudarle en esta situación, puede dejar vacío el parámetro Número de clústeres y permitir que la herramienta Clustering multivariante evalúe la eficacia de dividir las entidades en 2, 3, 4 y hasta 30 clústeres. La eficacia del clustering se mide mediante la pseudo estadística F Calinski-Harabasz, que es una proporción de la varianza entre clústeres respecto de la varianza dentro del clúster. En otras palabras, es una proporción que refleja la similitud dentro de un grupo y las diferencias entre grupos:

Método de clustering
La herramienta Clustering multivariante utiliza el algoritmo de valores medios K de forma predeterminada. El objetivo del algoritmo de valores medios K es dividir las entidades de manera que se minimicen las diferencias que existan entre las entidades de un clúster, en todos los clústeres. Debido a que el algoritmo es NP-duro, se utiliza una heurística codiciosa para clasificar las entidades en clústeres. El algoritmo codicioso siempre convergirá en un mínimo local, pero no siempre encontrará el mínimo global (más óptimo).
El algoritmo de valores medios K funciona identificando primero los valores de inicialización utilizados para hacer crecer cada clúster. Por consiguiente, el número de valores iniciales siempre coincidirá con el Número de clústeres. La primera semilla se selecciona de manera aleatoria. Sin embargo, la selección de las semillas que quedan, mientras aún se emplea un componente aleatorio, aplica una ponderación que favorece la selección de semillas posteriores más adelante en el espacio de datos desde el conjunto existente de entidades de semillas (esta parte del algoritmo se denomina valores medios K ++). Debido al componente aleatorio para buscar valores de inicialización cuando selecciona Ubicaciones de valores de inicialización optimizados o Ubicaciones de valores de inicialización aleatorios para el Método de inicialización, puede obtener variaciones en los resultados del clustering de una ejecución de la herramienta a la siguiente.
Una vez que se identifican los valores de inicialización, se asignan todas las entidades a la entidad valor de inicialización más cercana (más cercana en el espacio de datos). Para cada cluster de entidades, se calcula un centro medio de datos, y se vuelve a asignar cada entidad al centro más cercano. El proceso de calcular un centro medio de datos para cada clúster y luego reasignar las entidades al centro más cercano continúa hasta que se estabiliza la pertenencia al clúster (hasta un máximo de 100 iteraciones).
Al igual que el algoritmo de valores medios K, medoides K funciona identificando primero las entidades de valor de inicialización para hacer crecer cada clúster. Cada una de las entidades de valor de inicialización es una entidad real de Entidades de entrada. Estas entidades de valor de inicialización se denominan medoides. Todas las entidades se asignan al medoide más cercano (más cercano en el espacio de datos). Esta es la solución de clúster inicial. Se calcula la suma de la distancia (en el espacio de datos) entre el medoide y las entidades ajenas al medoide. Para afinar esta solución, dentro de cada clúster, el medoide se intercambia con cada entidad ajena al medoide y se calcula la suma de las distancias (en el espacio de datos) entre cada medoide y entidad ajena al medoide. Si el intercambio aumenta la suma de las distancias, se deshace a menos que la entidad intercambiada se convierta en el nuevo medoide. El proceso de buscar medoides nuevos y luego reasignar las entidades al medoide más cercano continúa hasta que se estabiliza la pertenencia al clúster.
Valores medios K y Medoides K son dos algoritmos de clustering populares y, por lo general, generan resultados similares. Sin embargo, Medoides K es más resistente al ruido y los valores atípicos de las Entidades de entrada. Valores medios K es por lo general más rápido que Medoides K y es preferible para los datasets grandes.
Salidas
La herramienta Clustering multivariante crea un número de resultados. Los mensajes son accesibles desde el panel Geoprocesamiento desplazando el puntero por encima de la barra de progreso, haciendo clic en el botón de progreso de herramienta  o expandiendo la sección de mensajes situada en la parte inferior del panel Geoprocesamiento. También puede acceder a los mensajes de una ejecución previa de Clustering multivariante a través del Historial de geoprocesamiento.
o expandiendo la sección de mensajes situada en la parte inferior del panel Geoprocesamiento. También puede acceder a los mensajes de una ejecución previa de Clustering multivariante a través del Historial de geoprocesamiento.

La salida predeterminada para la herramienta Clustering multivariante es una nueva clase de entidad de salida que contiene los campos que se utilizan en el análisis más un nuevo campo de tipo entero llamado CLUSTER_ID que identifica a qué clúster pertenece cada entidad. Esta clase de entidad de salida se agrega a la tabla de contenido con un esquema de representación en pantalla a color único aplicado al campo CLUSTER_ID. El campo IS_SEED indica qué entidades se eligieron como valores de inicialización y se usan para el desarrollo de los clústeres.

Salidas de gráfico de Clustering multivariante
Se crean varios tipos de gráficos para resumir los clústeres que se han creado. Se usan diagramas de caja para representar tanto las características de cada clúster como las características de cada variable utilizada en el análisis. El siguiente gráfico le muestra cómo interpretar los diagramas de caja y sus valores de resumen para cada Campo de análisis y clúster creado: valor mínimo de datos, 1.er cuartil, mediana global, 3.er cuartil, valor máximo de datos y valores atípicos de datos (valores más pequeños o más grandes que 1,5 veces el rango entre cuartiles). Sitúe el ratón sobre el diagrama de caja del gráfico para ver estos valores, así como el valor de rango entre cuartiles. Cualquier marca de punto que quede fuera del mínimo o el máximo (límite superior o inferior) representa valores atípicos de datos.
Explorar:
El rango entre cuartiles (IQR) es el 3.er cuartil menos el 1.er cuartil. Los valores atípicos bajos serían valores menores que 1.5*IQR (Q1-1.5*IQR) y los valores atípicos altos serían valores mayores que 1.5*IQR (Q3+1.5*IQR). Los valores atípicos aparecen en los diagramas de caja como símbolo de punto.

El gráfico de diagrama de caja paralelo predeterminado resume tanto los clústeres como las variables que contienen. Por ejemplo, la herramienta Clustering multivariante se ejecutó en distritos censales para crear cuatro clústeres. Observe en el gráfico siguiente que el clúster 2 (rojo) refleja distritos con rentas por encima de la media en comparación con el resto de clústeres, los valores más altos para los hogares liderados por mujeres con hijos (FHH_CHILD), los valores más altos para la cantidad de unidades residenciales (HSE_UNITS) y los valores más altos para los niños menores de 5 años. El clúster 4 (dorado) refleja distritos con las medianas de rentas más altas, casi el número más bajo de hogares con hijos con mujeres como cabeza de familia y más que la media de unidades de vivienda. El clúster 3 (verde) refleja los distritos con el menor número de hogares con hijos con mujeres como cabeza de familia, el menor número de hijos por debajo de los 5 años de edad, el menor número de unidades residenciales y casi la renta más baja (no tan baja como en el clúster 1). Sitúe el ratón sobre cada nodo de las líneas de media para ver el valor medio del clúster para cada Campo de análisis.

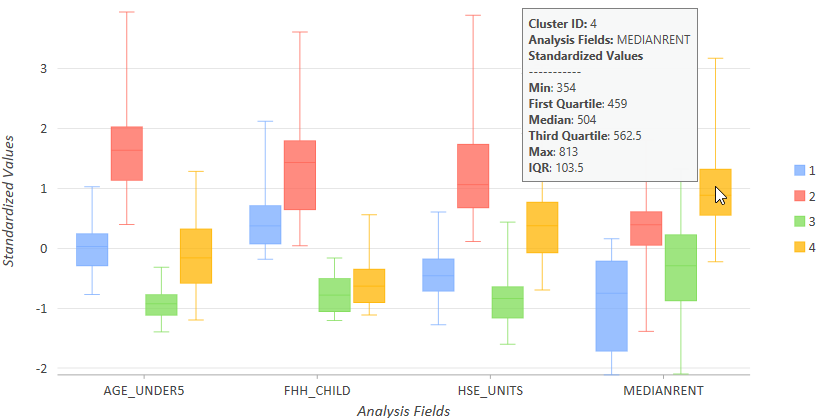
Tras inspeccionar el resumen global del análisis con los diagramas de caja paralelos que mostrábamos arriba, puede inspeccionar los diagramas de caja de cada clúster en cada variable, cambiando a En paralelo en la pestaña Series del panel Propiedades de gráfico. Con esta vista de los datos, es fácil ver qué grupo tiene el rango más alto y más bajo de valores en cada variable. Se crearán diagramas de caja para cada clúster y cada variable, de modo que puede ver la relación entre los valores de cada clúster y los de los demás clústeres creados. Sitúe el ratón sobre el diagrama de caja de cada variable para ver los valores Mínimo, Máximo y Mediana de cada variable de cada clúster. En el gráfico que aparece a continuación, por ejemplo, verá que el clúster 4 (dorado) presenta los valores más altos en la variable MEDIANRENT y contiene distritos con un rango de valores que va del 354 al 813.
También se crea un gráfico de barras que muestra el número de entidades por cada clúster. Al seleccionar cada barra, también se seleccionan las entidades del clúster en el mapa, lo que puede resultar útil para análisis posteriores.

Si deja vacío el parámetro Número de clústeres, la herramienta evaluará el número óptimo de clústeres basándose en sus datos. Si especifica una ruta para la Tabla de salida para evaluar el número de clústeres, se creará un gráfico que muestra los valores de la pseudo estadística F calculados. El pico más alto del gráfico es la estadística F más grande, que indica cuántos clústeres serán más eficaces para distinguir las entidades y las variables que especificó. En el gráfico que aparece a continuación, la estadística F asociada con cuatro grupos es la más alta. Cinco grupos, con una pseudo estadística F alta, también serían una buena elección.

Prácticas recomendadas
Aunque existe la tendencia a querer incluir tantos Campos de análisis como sea posible, para la herramienta Clustering multivariante funciona mejor comenzar con una variable única y construir. Los resultados son más fáciles de interpretar con menos campos de análisis. También es más fácil determinar qué variables son los mejores discriminadores cuando hay menos campos.
En muchos casos, es probable que ejecute la herramienta Clustering multivariante varias veces buscando el Número de clústeres óptimo y la combinación de Campos de análisis más eficaz y que mejor separe sus entidades por clústeres.
Si la herramienta devuelve 30 como número óptimo de clústeres, asegúrese de echar un vistazo al gráfico de la estadística F. Vale entras a la por la pregunta está en que hace Celia vamos a ver un poco o La selección del número de clústeres y la interpretación del gráfico de la estadística F es todo un arte y un número más bajo de clústeres podría ser más adecuado para su análisis.
Recursos adicionales
Consulte los siguientes recursos para obtener más información:
- Caliński, T. y J. Harabasz. 1974. "A dendrite method for cluster analysis." Communications in Statistics. 3:1, 1-27. https://doi.org/10.1080/03610927408827101.
- Hinde, A., T. Whiteway, R. Ruddick, y A. D. Heap. 2007. "Seascapes of the Australian Margin and adjacent sea floor: Keystroke Methodology." Geoscience Australia. Record 2007/10, 58pp.
- Jain, A. K. 2009. "Clustering de datos: 50 años más allá de los valores K.". Pattern Recognition Letters. https://doi.org/10.1016/j.patrec.2009.09.011.