Cómo funciona Detección de puntos de cambio

Para cada ubicación de un cubo de espacio-tiempo, la herramienta Detección de puntos de cambio identifica los periodos de tiempo cuando cambia alguna propiedad estadística de las series temporales. La herramienta puede detectar cambios en el valor medio, la desviación estándar o la pendiente (tendencia lineal) de variables continuas, así como cambios en el valor medio de las variables de recuento. La herramienta puede determinar el número de puntos de cambio de cada ubicación o se puede proporcionar un número definido de puntos de cambio que se utilizan en todas las ubicaciones.

Los puntos de cambio dividen cada serie temporal en segmentos en los que los valores de cada segmento tienen un valor medio, una desviación estándar o una tendencia lineal (pendiente e intercepción). Los puntos de cambio se definen como el primer periodo de tiempo de cada nuevo segmento empezando por el segundo segmento, de modo que el número de puntos de cambio siempre es uno menos que el número de segmentos.

Tipos de puntos de cambio

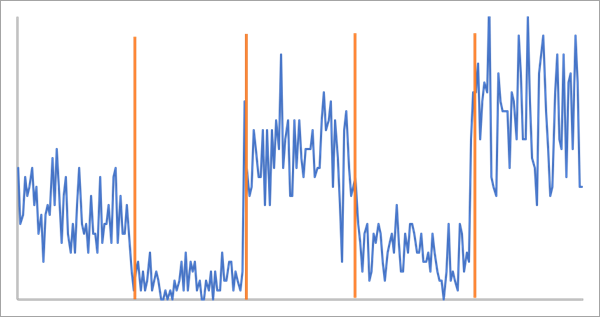
La herramienta puede detectar cuatro tipos de cambio. Cada imagen siguiente muestra las series temporales como un gráfico de líneas azul con líneas naranjas verticales en los puntos de cambio.

• Desplazamiento medio: detecta variaciones en el valor medio de la variable de análisis. Se supone que los valores de datos siguen una distribución normal, ya que todos los períodos de tiempo tienen la misma desviación estándar. El valor medio es constante dentro de cada segmento y cambia a un nuevo valor en cada punto de cambio.

  

  • Posible aplicación: detectar olas de calor cuando la temperatura máxima diaria aumenta a lo largo de un corto intervalo de tiempo.
• Desviación estándar: detecta cambios en la desviación estándar de la variable de análisis. Se supone que los valores de datos siguen una distribución normal, ya que todos los períodos de tiempo tienen el mismo valor medio. La desviación estándar es constante dentro de cada segmento y cambia a un nuevo valor en cada punto de cambio.

  

  • Posible aplicación: detectar cambios en la variación de velocidad del viento que podrían indicar eventos climatológicos importantes.
• Pendiente (tendencia lineal): detecta cambios en la tendencia lineal de la variable de análisis. Se supone que los valores de datos siguen una distribución normal con un valor medio definido por una línea y todos los periodos de tiempo tienen la misma desviación estándar. La pendiente y la intercepción de la línea son constantes dentro de cada segmento y cambian a valores nuevos en cada punto de cambio.

  

  • Posible aplicación: detecte cambios en la tendencia de los ingresos de las ventas a fin de determinar qué campañas de marketing son más efectivas.
• Recuento: detecta cambios en el valor medio de una variable de análisis que representa recuentos. Se supone que los valores de datos siguen una distribución Poisson dentro de cada segmento con un valor medio que cambia a un nuevo valor en cada punto de cambio.

  

  • Posible aplicación: detectar los cambios en los recuentos diarios de las tiendas a fin de estimar el comienzo y el final de cada estación de tránsito anual.

Salidas de la herramienta

La salida principal de la herramienta es una clase de entidad con una entidad para cada ubicación del cubo de espacio-tiempo de entrada. La capa se dibuja con cinco clases en función del número de puntos de cambio detectado en cada ubicación.

Las entidades de salida incluyen los siguientes campos:

• Número de puntos de cambio (NUM_CPTS): número de puntos de cambio detectados en la ubicación.
• Fecha del primer punto de cambio (FIRST_CHPT): fecha del primer punto de cambio en la ubicación. Si no se detectan puntos de cambio, el valor será nulo.
• Fecha del último punto de cambio (LAST_CHPT): fecha del último punto de cambio en la ubicación. Si no se detectan puntos de cambio, el valor será nulo. Si se detecta un punto de cambio, el valor será el mismo que la fecha del primer punto de cambio.

La hora de la capa de las entidades de salida se basa en la fecha del primer punto de cambio, de modo que el control deslizante de tiempo se puede utilizar para filtrar ubicaciones según esta fecha. La hora de la capa se puede cambiar a la fecha del último punto de cambio en las propiedades de capa. Esto se puede utilizar, por ejemplo, para animar a través del tiempo y visualizar en qué momento diferentes ubicaciones experimentan su primer o último punto de cambio para identificar patrones temporales en ubicaciones.

Gráficos emergentes de serie temporal

Al hacer clic en cualquier entidad del mapa usando la herramienta de navegación Explorar, se muestra un gráfico de líneas en el panel Elementos emergentes. El gráfico muestra un gráfico de líneas azul de la serie temporal en la ubicación con puntos de cambio indicados por puntos rojos más grandes.

Para los tipos de cambio cambio Desplazamiento medio y Recuento, las líneas rojas horizontales se dibujan en el valor medio de cada segmento.

Para el tipo de cambio Pendiente (tendencia lineal), se dibujan líneas rojas que muestran la tendencia lineal de cada segmento.

Para el tipo de cambio Desviación estándar, se dibuja una línea roja sólida con el valor medio global de toda la serie temporal. Para cada segmento, las líneas discontinuas rojas se dibujan dos desviaciones estándar por encima y por debajo del valor medio global con sombreado rosa entre las bandas. Estas bandas se ensanchan o se estrechan cuando la desviación estándar cambia en los puntos de cambio. Las líneas grises discontinuas se dibujan dos desviaciones estándar globales por encima y por debajo del valor medio global. Esto permite determinar si la desviación estándar de un segmento es mayor o menor que la desviación estándar de todas las series temporales.

Puede pasar el cursor por cualquier elemento del gráfico para obtener más información sobre los valores.

Nota:

Los gráficos emergentes no se crearán si las entidades de salida se guardan como shapefile (.shp).

Mensajes de geoprocesamiento

La herramienta proporciona varios mensajes con información sobre la ejecución de la herramienta. Los mensajes presentan varias secciones.

La sección Detalles del cubo de espacio-tiempo de entrada muestra propiedades del cubo de espacio-tiempo de entrada, junto con información sobre el intervalo del periodo de tiempo, número de periodos de tiempo, número de ubicaciones y número de bins de espacio-tiempo. Las propiedades mostradas en esta primera sección dependen de cómo se creó el cubo, por lo que la información varía en función del cubo.

La sección Fechas importantes muestra las fechas del primer y el último punto de cambio en todas las ubicaciones, así como la fecha con el mayor número de puntos de cambio. Se puede utilizar para identificar fechas en las que se produjeron grandes cambios que provocaban cambios en varias ubicaciones. Si hay vínculos, se muestra la primera fecha.

La sección Resumen de número de puntos por periodo de tiempo muestra el mínimo, el máximo, el valor medio, la mediana y la desviación estándar de la cantidad de puntos de cambio por periodo de tiempo. Esto le permite investigar la frecuencia de los puntos de cambio en las series temporales en todas las ubicaciones. Si la frecuencia es demasiado alta o demasiado baja, puede ajustar el valor del parámetro Sensibilidad de detección para aumentar o disminuir la frecuencia de los puntos de cambio.

Visualizar el cubo de espacio-tiempo en 3D

El cubo de espacio-tiempo de entrada se actualiza con los resultados del análisis y se puede utilizar en la herramienta Visualizar cubo de espacio-tiempo en 3D con la opción Cambiar puntos de serie temporal del parámetro Tema de visualización para mostrar los resultados en una escena 3D. La salida contendrá una entidad por periodo de tiempo del cubo de espacio-tiempo. Los periodos de tiempo detectados como puntos de cambio se etiquetan como Cambiar punto y se muestran en morado, y los periodos de tiempo no detectados como puntos de cambio se etiquetan como No cambiar punto y se muestran en gris claro.

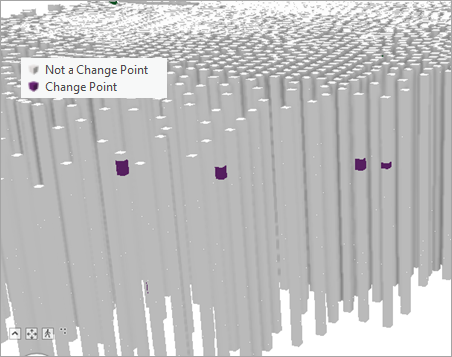
Se incluyen campos informativos sobre la hora, la ubicación y el Id. del periodo de tiempo junto con los siguientes campos sobre los puntos de cambio detectados:

• Cambiar indicador de punto (CHPT_IND): el campo contiene el valor 1 si el período de tiempo se detecta como un punto de cambio, y contiene 0 si el período de tiempo no se detecta como un punto de cambio.
• Valor medio actual (MEAN_CUR): valor medio del segmento que contiene el periodo de tiempo. Este campo solo se crea para el tipo de cambio de desplazamiento medio.
• Valor medio anterior (MEAN_BEF): valor medio del segmento que contiene el periodo de tiempo anterior. Los valores Valor medio actual y Valor medio anterior serán iguales si el período de tiempo no es un punto de cambio y serán diferentes si el período de tiempo es un punto de cambio (porque el valor anterior está en un segmento diferente). Esto le permite comparar los valores medios de los segmentos antes y después del punto de cambio. Este campo solo se crea para el tipo de cambio de desplazamiento medio.
• Desviación estándar actual (STDEV_CUR): desviación estándar del segmento que contiene el período de tiempo. Este campo solo se crea para el tipo de cambio de desviación estándar.
• Desviación estándar anterior (STDEV_BEF): desviación estándar del segmento que contiene el periodo de tiempo anterior. Los valores de Desviación estándar actual y Desviación estándar anterior serán iguales si el período de tiempo no es un punto de cambio y serán diferentes si el período de tiempo es un punto de cambio. Este campo solo se crea para el tipo de cambio de desviación estándar.
• Valor medio actual de recuentos (MEAN_CUR): valor medio de los recuentos del segmento que contiene el período de tiempo. Este campo solo se crea para el tipo de cambio de recuento.
• Valor medio de recuentos anteriores (MEAN_BEF): valor medio de los recuentos del segmento que contiene el periodo de tiempo anterior. Los valores Valor medio actual de recuentos y Valor medio de recuentos anterior serán iguales si el período de tiempo no es un punto de cambio y será diferente si el período de tiempo es un punto de cambio. Este campo solo se crea para el tipo de cambio de recuento.
• Pendiente actual (SLOPE_CUR): la pendiente de la línea del segmento que contiene el periodo de tiempo. Este campo solo se crea para el tipo de cambio de pendiente (tendencia lineal).
• Pendiente anterior (SLOPE_BEF): la pendiente de la línea del segmento que contiene el periodo de tiempo anterior. Este campo solo se crea para el tipo de cambio de pendiente (tendencia lineal).
• Intercepción actual (INTRCP_CUR): la intercepción de la línea del segmento que contiene el periodo de tiempo. Este campo solo se crea para el tipo de cambio de pendiente (tendencia lineal).
• Intercepción anterior (INTRCP_BEF): la intercepción de la línea del segmento que contiene el periodo de tiempo anterior. Este campo solo se crea para el tipo de cambio de pendiente (tendencia lineal).

Nota:

El tema de visualización Puntos de cambio de serie temporal de Visualizar cubo de espacio-tiempo en 2D volverá a crear la clase de entidad de salida requerida de la detección de puntos de cambio.

Cómo se detectan los puntos de cambio

El objetivo de la detección de puntos de cambio es encontrar periodos de tiempo en los que el valor medio, la desviación estándar o la pendiente de los datos cambia de un valor a otro. Este problema equivale al problema de la segmentación de series temporales, donde una serie temporal se divide en segmentos cuyos valores tienen un valor medio, desviación estándar o pendiente similares. Para determinar qué segmentación (conjunto de puntos de cambio) es óptima para una serie temporal, debe poder medir y comparar la eficacia de las distintas segmentaciones posibles. Esta comparación se realiza calculando un coste de segmentación para cada segmentación y la que tiene el coste más bajo es la más óptima.

El coste de una segmentación se calcula agregando los costes individuales de cada segmento de la segmentación, donde el coste de cada segmento se basa en una función de probabilidad determinada por el tipo de cambio (consulte Tipos de puntos de cambio para las suposiciones de distribución de cada tipo de cambio). De forma intuitiva, cuanto más cerca se aproximen los segmentos a la distribución supuesta del tipo de cambio, mayor será la probabilidad y menor será el coste de la segmentación.

Por ejemplo, la siguiente imagen muestra una serie temporal con 150 periodos de tiempo en los que todos los valores se generaron a partir de una distribución normal con una desviación estándar igual a 1. El valor medio de los primeros 50 periodos de tiempo es 0, entonces el valor medio aumenta a 10 para los 50 periodos de tiempo medios y luego disminuye de nuevo a 0 para los 50 periodos de tiempo finales. Los puntos de cambio se definen como los primeros periodos de tiempo en cada segmento nuevo, de modo que, para esta serie temporal, los periodos de tiempo 51 y 101 son los puntos de cambio verdaderos cuando la media se desplaza. Los histogramas de los segmentos individuales muestran que cada segmento parece seguir una distribución normal con una desviación estándar aproximadamente igual, pero un valor medio distinto, de modo que esta segmentación parece alinearse con las suposiciones del tipo de cambio de desplazamiento medio. Esto indica que la probabilidad de esta segmentación es alta y el coste de segmentación resultante es bajo. Para esta segmentación correcta, el coste de segmentación es 401,39 al detectar el desplazamiento medio. Este valor es difícil de interpretar por sí solo, pero se puede comparar con el coste de otras posibles segmentaciones.

La siguiente imagen muestra una segmentación incorrecta en la que se detectan períodos de tiempo 31 y 121 como puntos de cambio. El segmento central no aparece normalmente distribuido y tiene una desviación estándar mucho mayor que el primer y el último segmento. Esto sugiere que los valores de los datos de los segmentos son poco probables bajo la suposición de distribución del tipo de cambio de desplazamiento medio, por lo que el coste de la segmentación debe ser elevado. En realidad, el coste de esta segmentación es 2596,24, que es mucho mayor que el coste de la segmentación correcta. Esto confirma que estos puntos de cambio no son óptimos para esta serie temporal.

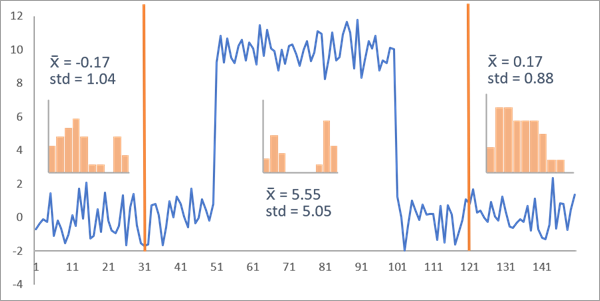
Ahora, supongamos que se agrega un punto de cambio innecesario además de los dos puntos de cambio verdaderos. En la siguiente imagen, los periodos de tiempo 51, 101 y 131 se identifican como puntos de cambio. Aunque el último punto de cambio no es necesario, los histogramas de segmento aparecen normalmente distribuidos con una desviación estándar aproximadamente igual, lo que indica una probabilidad alta y un coste de segmentación bajo. El coste de esta segmentación es 401,27, que es ligeramente inferior al coste de la segmentación real (401.39). La segmentación con un punto de cambio innecesario presenta un coste de segmentación menor que la segmentación real porque las probabilidades nunca decrecen incluyendo nuevos parámetros (en este caso, nuevos puntos de cambio). La inclusión del punto de cambio adicional solo redujo ligeramente el coste porque proporcionó muy poca mejora en cuanto al ajuste del modelo a los datos, en comparación con no incluirse como punto de cambio.

Si no se aplican restricciones al número de puntos de cambio, el coste de la segmentación siempre se reducirá agregando más puntos de cambio. Para evitar que todos los períodos de tiempo se detecten como puntos de cambio, debe aplicar uno de los dos tipos de restricciones utilizando el parámetro Método.

La opción Número definido de puntos de cambio (SegNeigh) permite especificar cuántos puntos de cambio se detectarán mediante el parámetro Número de puntos de cambio. Esta opción utiliza el algoritmo Segmento Vecindad (SegNeigh, Auger 1989) para buscar la segmentación con el coste más bajo entre todas las segmentaciones posibles que tengan el número especificado de puntos de cambio.

La opción Detectar automáticamente el número de puntos de cambio (PELT) utiliza el algoritmo Hora lineal exacta ejecutada (PELT, Killick 2012) para estimar el número y la ubicación de los puntos de cambio. Este algoritmo penaliza la inclusión de cada punto de cambio adicional agregando un valor de penalización al coste de cada segmento y buscando la segmentación cuyo coste penalizado (coste de segmentación más penalización) es el más pequeño entre todas las segmentaciones posibles. La intuición detrás de PELT es que, para que un período de tiempo se detecte como un punto de cambio, debe reducir el coste de la segmentación en más del valor de penalización que se agrega. Si la reducción de coste es menor que la penalización agregada, el coste penalizado aumentará y el período de tiempo no se detectará como un punto de cambio.

La elección del valor de penalización es fundamental para los resultados de PELT. Las penalizaciones que son demasiado bajas pueden detectar muchos puntos de cambio falsos, y las penalizaciones que son demasiado altas pueden no detectar puntos de cambio reales. El valor de penalización utilizado en PELT está determinado por el valor del parámetro Sensibilidad de detección. La sensibilidad se proporciona como un número entre 0 y 1, donde las diferencias más altas detectan más puntos de cambio usando valores de penalización más bajos. Cada ubicación del cubo de espacio-tiempo utilizará el mismo valor de penalización al detectar puntos de cambio.

Para el cambio de valor medio, desviación estándar y recuento, el valor de penalización se determina a partir de la sensibilidad mediante la siguiente fórmula, donde n es el número de periodos de tiempo de la serie temporal:

El valor de sensibilidad más alto de 1 corresponde a minimizar el Criterio de información bayesiano (BIC).

Para el cambio de pendiente (tendencia lineal), se utiliza una fórmula de penalización más conservadora:

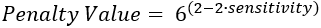
El valor de sensibilidad predeterminado de 0,5 corresponde a minimizar el Criterio de información de Akaike (AIC). El cambio de pendiente (tendencia lineal) utiliza una fórmula de penalización más conservadora porque otros tipos de cambio tienen dificultades para diferenciar entre tendencias y puntos de cambio, por lo que requieren valores de penalización más elevados para evitar detectar demasiados puntos de cambio. Sin embargo, el cambio de pendiente (tendencia lineal) se ha diseñado para datos con tendencias y no requiere valores de penalización tan elevados.

PELT y SegNeigh son algoritmos recursivos exactos, lo que significa que siempre devolverán la segmentación con el menor coste global de segmentación, dado un valor de penalización fijo o un número fijo de puntos de cambio. Los algoritmos se realizan de forma independiente en todas las ubicaciones del cubo de espacio-tiempo de entrada.

Existe una correspondencia entre PELT y SegNeigh en el sentido de que detectarán los mismos periodos de tiempo que los puntos de cambio si ambos métodos detectan el mismo número de puntos de cambio. Por ejemplo, si realiza PELT y utiliza un valor de penalización que detecta seis puntos de cambio en una ubicación, después realiza SegNeigh y especifica que se detectarán seis puntos de cambio, ambos métodos detectarán los mismos períodos de tiempo como puntos de cambio.

Longitud mínima de segmento

Puede utilizar el parámetro Longitud mínima de segmento para especificar el número mínimo de periodos de tiempo dentro de cada segmento. Por ejemplo, si tiene ingresos de ventas diarios y especifica una longitud mínima de segmento de 7, habrá al menos una semana entre cada punto de cambio. El valor predeterminado de la longitud mínima de segmento es el valor más pequeño necesario para calcular el coste del segmento. El valor predeterminado de cambio de la media, la desviación estándar y el recuento es 1, lo que significa que cada periodo de tiempo puede ser un punto de cambio. Para el cambio de pendiente (tendencia lineal), el valor predeterminado es 2 porque se requieren al menos dos periodos de tiempo para ajustar una línea a los valores del segmento.

La longitud mínima del segmento es otra restricción además de la restricción aplicada con el parámetro Método. PELT o SegNeigh encontrará el conjunto de puntos de cambio con el menor coste de segmentación entre todas las segmentaciones posibles cuyos segmentos tienen al menos la longitud mínima.

Prácticas recomendadas y limitaciones

Debe tener en cuenta varias consideraciones a la hora de elegir los parámetros y opciones de la herramienta.

• Los métodos de modificación de puntos se clasifican en línea o sin conexión y esta herramienta realiza la detección sin conexión. Los métodos sin conexión suponen una serie temporal existente con un inicio y un final, y el objetivo es volver atrás en el tiempo para determinar cuándo se produjeron los cambios. En su lugar, los métodos en línea se ejecutan constantemente en los datos que se actualizan a medida que hay nuevos valores disponibles. El objetivo de los métodos de detección en línea es detectar en directo nuevos cambios en el tiempo mínimo posible después de que se haya producido el cambio. Los métodos en línea y sin conexión difieren significativamente en sus algoritmos, casos de uso y suposiciones sobre los datos.
• Detectar cambios de valor medio, desviación estándar o recuento es más eficaz para datos sin tendencias y cuyos cambios se produzcan en un solo periodo de tiempo. Para las series temporales con tendencias, se pueden detectar muchos periodos de tiempo como puntos de cambio debido al valor medio que cambia constantemente. Del mismo modo, si el cambio es más gradual y tarda varios períodos de tiempo antes de que el valor cambie completamente, todos los períodos de tiempo durante la transición se pueden detectar como puntos de cambio. Para estos casos, se recomienda utilizar valores más bajos para el parámetro Sensibilidad de detección o para detectar cambios de pendiente (tendencia lineal).
• La detección de puntos de cambio es similar a la detección de valores atípicos de serie temporal, pero difiere en aspectos importantes. La detección de puntos de cambio identifica los periodos de tiempo cuando un modelo cambia a un nuevo modelo (por ejemplo, un cambio en el valor medio) y la detección de valores atípicos identifica periodos de tiempo que se desvían significativamente de un modelo único. La primera sugiere un cambio agresivo, mientras que esta última sugiere una anomalía a corto plazo.

• Para las variables de análisis que representan recuentos, la opción Recuento del parámetro Tipo de cambio suele ser más adecuada para detectar cambios en el valor medio de los recuentos. Sin embargo, la opción Desplazamiento medio puede proporcionar resultados equivalentes o mejores para los datos de recuento. Esto se debe a que el modelo del tipo de cambio de recuento presupone que los valores de cada segmento siguen una distribución Poisson en la que la varianza del segmento es igual al valor medio del segmento. En su lugar, el tipo de cambio de desplazamiento medio presupone que los valores de cada segmento están distribuidos normalmente, de modo que el valor medio puede ser mayor o menor que la varianza de los valores.

  En una distribución Poisson, la mayoría de los recuentos están dentro de aproximadamente dos raíces cuadradas del valor medio. Por ejemplo, para una distribución Poisson con un valor medio igual a 100, aproximadamente el 95 por ciento de los recuentos estará entre 80 y 120 (2 × sqrt(100) = 20). Para una distribución Poisson con un valor medio igual a 1 millón, la mayoría de recuentos estará entre 998.000 y 1.002.000 (la raíz cuadrada de 1 millón es 1.000). El rango de recuentos es en comparación más acotado para el valor medio más grande de 1 millón, donde la mayoría de los recuentos están dentro del 0,2 por ciento del valor medio. Sin embargo, en el valor medio más pequeño de 100, los recuentos varían hasta el 20 por ciento del valor medio. Comparados con su valor medio, si los valores de los recuentos varían más de lo esperado respecto de una distribución Poisson, es posible que se detecten muchos periodos de tiempo como puntos de cambio. Esto es más común con recuentos grandes. En este caso, se recomienda que detecte el desplazamiento medio.

• Para todos los tipos de cambio, el primer período de tiempo nunca se detectará como un punto de cambio. Esto se debe a que los puntos de cambio marcan el inicio de cada segmento nuevo, comenzando por el segundo segmento. Dado que el primer intervalo de tiempo siempre está en el primer segmento, nunca puede ser un punto de cambio. Además, para el cambio de pendiente (tendencia lineal), los dos primeros periodos de tiempo nunca se detectarán como puntos de cambio porque debe haber al menos dos periodos de tiempo en el primer segmento.
• Para la opción Número definido de puntos de cambio (SegNeigh) del parámetro Método, la segmentación óptima no siempre es única. Si varias segmentaciones tienen el mismo coste de segmentación, se devolverán los puntos de cambio óptimos más recientes posibles. Por ejemplo, si todos los valores de una serie temporal son iguales en una ubicación, todas las segmentaciones tienen la misma probabilidad y coste. En este caso, si se solicitan tres puntos de cambio, los tres últimos periodos de tiempo se detectarán como puntos de cambio en la ubicación.
• La detección del desplazamiento de la media requiere la estimación de la varianza de los datos en torno a la media sin conocer los periodos de tiempo en los que se desplaza la media (los puntos de cambio). Las fórmulas de varianza tradicionales están sesgadas en presencia de una media cambiante desconocida, por lo que se utiliza la siguiente fórmula de varianza sólida:

  

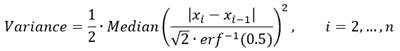
  Detectar cambios en la pendiente también requiere estimar una varianza desconocida alrededor de una línea de tendencia cambiante, y se utiliza la siguiente fórmula de varianza sólida:

  

  Si alguna de las fórmulas da como resultado cero, la varianza se estima suponiendo que no hay conversiones ni tendencias en el valor medio.

Recursos adicionales

Para obtener más información sobre la detección de puntos de cambio, consulte las siguientes referencias:

• Auger, I. E. and Lawrence, C. E. (1989). "Algorithms for the optimal identification of segment neighborhoods."Bulletin of Mathematical Biology. 51(1):39-54. https://doi.org/10.1007/BF02458835
• Killick, R., Fearnhead, P., and Eckley, I.A. (2012). "Optimal Detection of Changepoints With a Linear Computational Cost." Journal of the American Statistical Association. 107. 1590-1598. https://dx.doi.org/10.1080/01621459.2012.737745
• Killick, R. and Eckley, I.A. (2014). "changepoint: An R Package for Changepoint Analysis." Journal of Statistical Software. https://dx.doi.org/10.18637/jss.v058.i03