Cómo funciona Suavizado con conservación de entidades

Disponible con una licencia de Spatial Analyst.

La herramienta Suavizado con conservación de entidades suaviza un ráster de superficie de entrada, como los rásters de modelo digital de elevación (DEM) o de modelo de superficie digital (DSM). El ráster resultante es una versión suavizada del DEM original del que se ha eliminado el ruido (como pequeñas protuberancias, hoyos y rupturas de pendiente de baja inclinación) sin alterar significativamente otras entidades del paisaje.

La herramienta tiene varios parámetros de entrada que le permiten controlar el proceso de suavizado, como la distancia de vecindad de entrada, el umbral de diferencia normal de entrada, el número de iteraciones de entrada y el umbral de cambio máximo de elevación de entrada. Cada uno de estos parámetros controla una perspectiva única del proceso de suavizado o de conservación de entidades. Pero con frecuencia es necesario utilizarlos combinados para obtener la suavidad de salida deseada.

Distancia de vecindad

El parámetro Distancia de vecindad define el tamaño de vecindad utilizado por el algoritmo de suavizado. Puede especificarse como número de celdas o como distancia en el mapa, en función de la configuración del parámetro Unidades de distancia. Se mide desde el centro de la celda de procesamiento actual hasta el centro de un vecino ortogonal. La menor distancia de vecindad permitida es de 1 celda (o igual al tamaño de celda del ráster de entrada si se especifica mediante un valor de distancia), lo que da como resultado una ventana de 3 por 3 celdas.

Se muestra la relación entre la distancia de la vecindad (línea naranja) y el número de celdas de la ventana en movimiento. Para un tamaño de celda de 10 metros, una distancia de vecindad de 10 metros utilizará una ventana de 3 por 3 celdas. Una distancia de vecindad de 20 metros utilizará una ventana de 5 por 5 celdas, y una distancia de vecindad de 30 metros utilizará una ventana de 7 por 7 celdas.

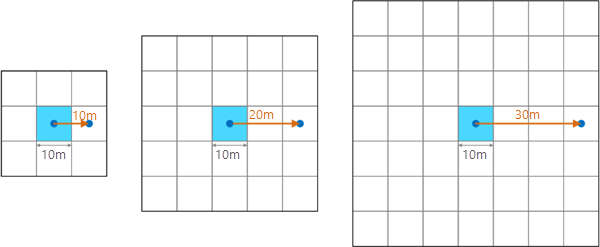
Si se especifica una distancia de vecindad que no resulta en un intervalo entero de tamaños de celda, se redondeará al siguiente intervalo de tamaños de celda. Por ejemplo, para un tamaño de celda de 10 metros, si se especificó una distancia de vecindad de 19 metros, el algoritmo redondeará al siguiente intervalo del tamaño de celda, 20 metros (dos veces el tamaño de celda), lo que dará como resultado una ventana de 5 por 5 celdas.

El tamaño de la vecindad afecta a la eficacia del algoritmo de suavizado. Una vecindad más amplia puede aumentar la suavidad general del resultado. Una vecindad más pequeña permite que la herramienta se centre más en la variabilidad local del paisaje, lo que hace que se suavicen las pequeñas entidades. Dado que el ruido suele ser un fenómeno a pequeña escala, normalmente el tamaño de la vecindad debe ser pequeño. Por ejemplo, un valor de 5 para el parámetro Distancia de vecindad, que da como resultado una ventana de procesamiento de 11 por 11 celdas, suele ser eficaz para garantizar que solo se suavice el ruido.

Se muestra el efecto de las distancias de vecindad en la suavidad de la salida. De izquierda a derecha: la primera imagen muestra el ráster de superficie de entrada de 1 metro de resolución; la segunda imagen muestra la salida con una distancia de vecindad de 2 celdas; la tercera imagen muestra la salida con una distancia de vecindad de 5 celdas.

Umbral de diferencia normal

Con la herramienta Suavizado con conservación de entidades, el algoritmo de filtrado calcula la media ponderada sobre los vectores normales en lugar de sobre los valores de las celdas. Un vector normal es un vector 3D perpendicular al plano tangente en la ubicación de una celda, con una magnitud de 1. La siguiente imagen ilustra un vector normal de superficie en una vista de sección cruzada:

Una vista de sección cruzada muestra un vector normal de superficie en el punto T.

La herramienta calcula un campo vectorial normal para todas las celdas de la vecindad de la celda de procesamiento actual. Una diferencia normal se define como el ángulo formado entre el vector normal de la celda de procesamiento actual y el vector normal de una celda vecina. La siguiente imagen muestra un ejemplo de campo vectorial normal y diferencia normal:

Se muestra el campo vectorial normal para un ejemplo de vecindad de 5 por 5. El subconjunto ilustra un caso de la diferencia normal (θ) entre la celda actual (morado) y una celda vecina (verde).

No todas las celdas vecinas se utilizarán en el filtrado. El algoritmo de filtrado utiliza el parámetro Umbral de diferencia normal para determinar qué celdas vecinas se utilizarán (solo se utilizarán aquellas celdas cuya diferencia normal con la celda actual sea menor que el ajuste de este parámetro).

El parámetro Umbral de diferencia normal representa un umbral para la conservación de la inclinación de los bordes. Los bordes de entidad más planos que este valor pueden suavizarse. Los bordes de entidad que tengan una pendiente superior a este valor se conservan. En la mayoría de los casos, debe especificarse un valor pequeño (como 15 grados o menos) para este parámetro a fin de garantizar que solo se suavizan las entidades planas.

Se muestra el efecto del umbral de diferencia normal en los bordes de la entidad de salida. De izquierda a derecha: la primera imagen muestra el ráster de superficie de entrada de 1 metro de resolución; la segunda imagen muestra la salida con un umbral de diferencia normal de 5 grados; la tercera imagen muestra la salida con un umbral de diferencia normal de 30 grados.

Numero de iteraciones

Una sola aplicación del proceso de suavizado puede no lograr el grado de suavizado de salida necesario. Especificar un valor superior a 1 para el parámetro Número de iteraciones permite a la herramienta repetir varias veces el proceso de suavizado.

El efecto acumulado aumentará la suavidad del ráster de salida, a costa de un tiempo de procesamiento adicional. En la mayoría de los casos, un valor pequeño (como 3) debería funcionar bien.

Se muestra el efecto de icrementar el número de iteraciones sobre la suavidad de la salida. De izquierda a derecha: la primera imagen muestra el ráster de superficie de entrada de 1 metro de resolución; la segunda imagen muestra la salida tras una iteración; la tercera imagen muestra la salida tras cinco iteraciones.

Cambio máximo de elevación

El parámetro Cambio máximo de elevación le permite definir el cambio máximo permitido de los valores de las celdas de una iteración.

Este parámetro representa un umbral para los cambios de altura de la entidad. Las entidades más cortas que este valor pueden suavizarse. Las entidades más altas que este valor se conservan. En la mayoría de los casos, debe especificarse un valor pequeño (como 0,5 metros) para este parámetro a fin de garantizar que solo se suavicen las entidades cortas.

Se muestra el efecto del cambio máximo de elevación en la conservación de la entidad. De izquierda a derecha: la primera imagen muestra el ráster de superficie de entrada de 1 metro de resolución; la segunda imagen muestra la salida con un cambio máximo de elevación de 0,05 metros; la tercera imagen muestra la salida con un cambio máximo de elevación de 1,0 metros.

Algoritmo de suavizado con conservación de entidades

La herramienta Suavizado con conservación de entidades se basa en un planteamiento vectorial normal 3D que suaviza los rásteres DEM (véase Lindsay et al, 2019).

Para una celda determinada, un vector normal 3D, n = (a, b, c), es un vector perpendicular al plano tangente en la ubicación de la celda. El plano se define mediante la siguiente ecuación:

ax + by + cz + d = 0

La herramienta calcula primero un vector normal para cada celda de la vecindad de la celda actual.

A continuación, para la celda actual, realiza una media ponderada de los vectores normales de las celdas vecinas. El peso de una celda vecina j se determina del siguiente modo:

Si θ_j es inferior a θ_t, se aplica la siguiente ecuación:

• Donde:

  θ_j es la diferencia normal entre la celda actual y la vecina j

  θ_t es el umbral de diferencia normal

Si θ_j es mayor o igual que θ_t, entonces W_j = 0, lo que excluye a la celda vecina j de la media ponderada.

Por último, se utiliza el vector normal de superficie suavizada para obtener un nuevo valor de altura en la ubicación actual de la celda sustituyendo a, b y c en la primera ecuación y se resuelve para z.

Cuando el nuevo valor z se utiliza para actualizar el valor en la ubicación de una celda, se compara con el valor de elevación original en esa ubicación. Si la diferencia no es mayor que el valor del parámetro de entrada Cambio máximo de elevación, se utilizará el nuevo valor z. De lo contrario, el valor de elevación original permanece inalterado. El proceso de suavizado se repite el número de veces definido por el valor del parámetro de entrada Número de iteraciones.

Utilización de una GPU

Esta herramienta puede aumentar el rendimiento si tiene determinado hardware de GPU instalado en su sistema. Consulte el tema Procesamiento de GPU con Spatial Analyst para obtener más información sobre la compatibilidad de esta capacidad y sobre el procedimiento para configurarla y activarla.

Referencias

Lindsay, John B., Anthony Francioni y Jaclyn M. H. Cockburn. 2019. "LiDAR DEM Smoothing and the Preservation of Drainage Features." Remote Sensing 11, número 16, 1926. https://doi.org/10.3390/rs11161926

Sun, Xiangfang, Paul L. Rosin, Ralph Martin y Frank Langbein. 2007. "Fast and effective feature-preserving mesh denoising." IEEE Transactions on Visualization and Computer Graphics Volumen 13, número 5. pp. 925–938. https://doi.org/10.1109/TVCG.2007.1065