Funcionamiento de la herramienta Asociación espacial bivariante (L de Lee)

La herramienta Asociación espacial bivariante (L de Lee) mide la asociación espacial (dependencia) entre dos variables de análisis continuas calculando el valor estadístico L de Lee. El valor estadístico caracteriza el grado de correlación de las variables y su copatterning (similitud de agrupación espacial). El valor estadístico L de Lee estará comprendido entre -1 y 1 y es conceptualmente similar a un coeficiente de correlación, pero se ajusta para tener en cuenta la autocorrelación espacial de las dos variables. Los valores L de Lee cercanos a 1 indican que las variables están muy correlacionadas positivamente (cuando un valor es alto, el otro tiende a serlo también) y que cada variable tiene una alta autocorrelación espacial (los valores altos y bajos de las variables tienden a agruparse). Los valores próximos a -1 indican que las variables están muy correlacionadas negativamente (cuando un valor es alto, el otro tiende a ser bajo) y que cada variable tiene una autocorrelación espacial alta. Los valores próximos a 0 indican que las variables no están asociadas espacialmente, lo que significa que no están correlacionadas o que no están autocorrelacionadas espacialmente. El valor estadístico también se puede particionar localmente para cada entidad de entrada y categorizar, lo que permite investigar cómo cambia la asociación espacial de las variables de análisis a lo largo de un área de estudio.

Tener en cuenta la autocorrelación espacial de las variables es esencial para evaluar la asociación espacial entre las variables de análisis, ya que las pruebas estadísticas tradicionales basadas en la correlación de Pearson no son válidas cuando las variables están espacialmente autocorrelacionadas. Además, estas pruebas tradicionales no evalúan el factor copatterning de las dos variables, que es un aspecto crítico de la relación espacial entre las variables.

El valor estadístico L de Lee se calcula combinando la correlación de las medias locales de vecindario de las dos variables de análisis y ajustando la correlación mediante escalares de suavizado espacial de cada variable de análisis. Los escalares de suavizado espacial son valores entre 0 y 1. Los escalares de suavizado cercanos a 1 indican una fuerte autocorrelación espacial (positiva o negativa), y los valores cercanos a 0 indican que los valores son espacialmente aleatorios y no autocorrelacionados. Los escalares de suavizado espacial pequeños reducirán el valor estadístico L de Lee en relación con la correlación de Pearson para ajustar la falta de agrupación espacial de las variables.

Las siguientes imágenes muestran varios ejemplos de mapas de dos variables de análisis y las correlaciones de Pearson y los valores estadísticos L de Lee asociados para las variables. En cada imagen, los triángulos azules tienen el valor 1, y los triángulos naranjas, el valor 0.

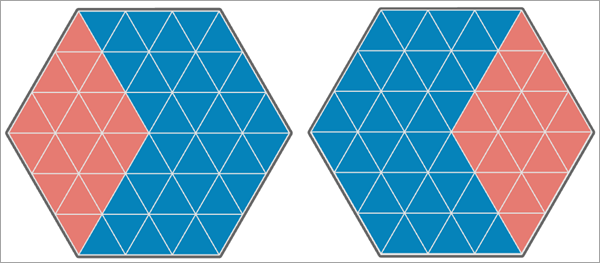
En la primera imagen de abajo, ambas variables de análisis tienen los mismos valores en cada ubicación, por lo que su correlación de Pearson es igual a 1. Además, cada una de ellas tiene una alta autocorrelación espacial positiva con valores altos y bajos agrupados. El da lugar a un valor estadístico L de Lee igual a 0,801, lo que indica una elevada asociación espacial positiva entre las variables.

En la segunda imagen, los valores de la segunda variable de análisis se desplazan un triángulo a la derecha, de modo que 30 de los 54 triángulos tienen valores coincidentes. El resultado es una correlación de Pearson igual a 0,167. Sin embargo, debido a la fuerte autocorrelación espacial de cada variable de análisis, el valor estadístico L de Lee es ligeramente superior: 0,186. Esto indica una asociación espacial positiva de débil a moderada entre las variables.

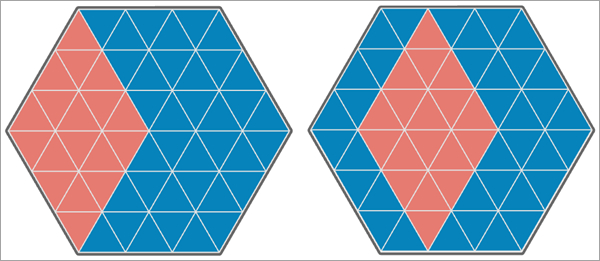
En la tercera imagen, los valores de la segunda variable de análisis se desplazan al otro lado del área de estudio hexagonal, y 18 de los 54 triángulos tienen valores coincidentes. El resultado es una correlación de Pearson igual a -0,500, y el valor estadístico L de Lee es igual a -0,490, lo que indica una asociación espacial negativa de moderada a fuerte entre las variables.

En la imagen final, ambas variables de análisis tienen autocorrelación espacial negativa, y ninguno de los triángulos tiene el mismo valor. El resultado es una correlación de Pearson igual a -1, y el valor estadístico L de Lee es igual a -0,204, lo que indica una asociación espacial negativa de débil a moderada entre las variables.

Valores estadísticos L de Lee locales

El valor estadístico L de Lee puede particionarse para cada entidad de entrada para ver cómo cambia espacial y localmente la asociación espacial entre las variables. Algunas regiones o ubicaciones pueden tener una asociación espacial mayor o menor que el valor estadístico L de Lee general (global) debido a las correlaciones locales cambiantes y al suavizado espacial local. Puede determinar si la asociación espacial local es mayor o menor que la asociación espacial global comparando directamente el valor estadístico L de Lee local con el valor estadístico L de Lee global. A diferencia del valor estadístico global, los valores estadísticos locales pueden ser mayores que 1 o menores que -1, y la media de los valores estadísticos locales siempre es igual al valor estadístico global.

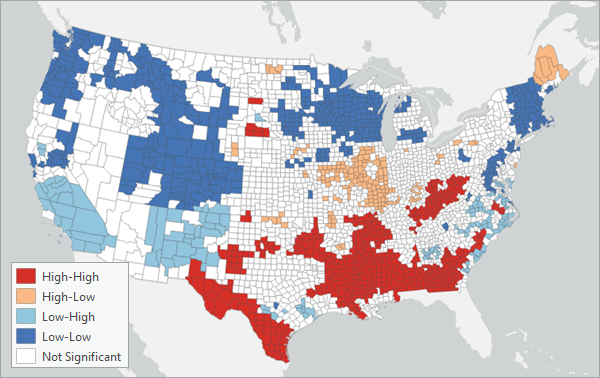
También puede clasificar los valores estadísticos L de Lee locales en varias categorías en función de su importancia estadística y de los valores de las vecindades de cada entidad. Hay cinco categorías posibles para cada entidad: Not Significant, High-High, High-Low, Low-High y Low-Low. Si el valor estadístico L de Lee local no es significativo al menos en un 90 % para una entidad, se clasificará como No significativo. En caso contrario, si el promedio del vecindario de la primera variable de análisis es mayor que el promedio de la primera variable de análisis, el promedio del vecindario de la segunda variable es mayor que el promedio de la segunda variable, se clasificará como High-High. Del mismo modo, si la primera variable es inferior al promedio, y la segunda es superior al promedio, se clasificará como Low-High (y viceversa). Es importante distinguir estas categorías, ya que, si las dos variables están asociadas espacialmente de forma positiva, significa que los valores bajos de las dos variables tienden a agruparse juntos y los valores altos tienden a agruparse juntos. Sin embargo, ambas situaciones darán lugar a grandes valores estadísticos L de Lee locales, por lo que las categorías aclaran si cada entidad tiene una asociación alta porque ambas variables son altas o porque ambas variables son bajas. Del mismo modo, para la asociación espacial negativa, las clasificaciones aclaran si una entidad tiene un valor estadístico L de Lee local negativo porque la primera variable es alta y la segunda baja, o si la primera variable es baja y la segunda alta.

Cuando se ejecuta en un mapa activo, la capa de entidades de salida dibujará basándose en estas cinco categorías. Para las variables asociadas espacialmente de forma positiva (valor estadístico global L de Lee mayor que 0), la capa contendrá principalmente categorías High-High y Low-Low. Para las variables asociadas espacialmente de forma negativa (valor estadístico L de Lee global inferior a 0), la capa contendrá principalmente categorías High-Low y Low-High.

Casos de uso de ejemplo

Puede utilizar la herramienta en los siguientes escenarios:

• Investigar la asociación espacial entre los niveles educativos y la renta familiar en distintos vecindarios de una gran ciudad. ¿Corresponden las zonas con mayor nivel educativo a las zonas con mayores ingresos familiares?
• Investigar la asociación espacial entre la cobertura vegetal y la calidad del aire. ¿Las zonas con más vegetación suelen tener una mejor calidad del aire? ¿Es la asociación estadísticamente significativa?
• ¿Existe una relación entre los índices de delincuencia y el valor de la propiedad? ¿Cambia la relación en las distintas regiones de un área metropolitana?

Permutaciones y valores p

Puede comprobar la significación estadística de los valores estadísticos L de Lee globales y locales mediante permutaciones. Las permutaciones reasignan aleatoriamente todos los valores de las dos variables de análisis a una nueva ubicación (manteniendo los dos valores emparejados en cada nueva ubicación), y se calculan los valores estadísticos L de Lee globales y locales para los valores permutados. Este proceso se repite un gran número de veces (controlado por el valor del parámetro Número de permutaciones), lo que crea distribuciones de referencia que se pueden comparar con los valores estadísticos L de Lee globales y locales originales. Si el valor original se encuentra en los extremos (derecho o izquierdo) de la distribución de referencia, significa que es poco probable que el valor original sea el resultado de una variación aleatoria, y que la asociación espacial es estadísticamente significativa. El valor p del valor estadístico L de Lee global se devuelve en forma de mensaje de geoprocesamiento, y los valores p y los niveles de significación de los valores estadísticos L de Lee locales se devuelven en forma de campos de la clase de entidad de salida. Consulte la sección Salidas de herramientas que aparece a continuación para obtener más información.

Nota:

Los valores p se calculan contando el número de valores permutados que son más extremos que el valor original, sumando uno y dividiendo por el número de permutaciones más uno. Este ajuste del numerador y el denominador se realiza para tener en cuenta las muestras pequeñas y garantizar que los valores p nunca sean iguales a cero. A continuación, el valor se duplica para que el valor p proceda de una prueba de hipótesis bilateral. El lado de la prueba se determina por el lado que tiene una menor proporción de valores más extremos (valores permutados que son mayores o menores que el valor original). Los valores p de los valores estadísticos L de Lee locales no se ajustan para pruebas de hipótesis múltiples, así que téngalo en cuenta al interpretar cualquier valor p local concreto.

Tipos de vecindad

Los valores estadísticos L de Lee global y local requieren un vecindario alrededor de cada entidad para estimar la asociación espacial. Puede especificar el vecindario de cada entidad mediante el parámetro Tipo de vecindad. El parámetro tiene las opciones que se describen a continuación para definir las entidades que se utilizan como vecinas de cada entidad. Para todos los tipos de vecindario, la entidad se incluye en su propio vecindario.

• Banda de distancia fija: se utilizarán como vecinos todas las entidades existentes dentro de una distancia especificada (hasta un máximo de 1000 entidades). Este valor predeterminado es la distancia euclidiana que garantiza que cada entidad tenga como mínimo un vecino. Especifique la distancia en el parámetro Banda de distancia. En el caso de los polígonos, se utilizarán las distancias entre centroides para determinar los vecinos.

  

• Vecinos K más cercanos: se utilizará como vecinos un número fijo de entidades más cercanas a la entidad focal. Especifique el valor en el parámetro Número de vecinos. Este valor no incluye la entidad en sí, por lo que el número de entidades utilizadas en los cálculos será una más que el valor especificado. En el caso de los polígonos, se utilizarán las distancias entre centroides para determinar los vecinos.

  

• Solo bordes de contigüidad: se utilizará como vecino cualquier polígono que comparta un borde con la entidad. Esta opción solo es aplicable a las entidades poligonales.

  

• Bordes o esquinas de contigüidad: se utilizará como vecino cualquier polígono que comparta un borde o esquina con la entidad. Esta opción solo es aplicable a las entidades poligonales.

  

• Triangulación de Delaunay: los vecinos se determinarán compartiendo bordes o esquinas en su triangulación de Delaunay (polígonos de Thiessen) recortada en el casco convexo de los puntos. Esta opción solo está disponible para las capas de entidades de puntos.

  

• Obtener ponderaciones espaciales a partir del archivo: los vecinos y las ponderaciones de cada entidad se definirán mediante un archivo de matriz de ponderaciones espaciales especificado en el parámetro Archivo de matriz de ponderaciones. Puede crear el archivo mediante las herramientas Generar matriz de ponderaciones espaciales o Generar ponderaciones espaciales de red.

Para la banda de distancia y los vecindarios de número de vecinos, los vecinos más cercanos a la entidad pueden recibir ponderaciones más altas utilizando una función kernel que disminuye con la distancia. Para aplicar las ponderaciones más grandes a los vecinos más cercanos, especifique la opción Bicuadrado para el parámetro Esquema de ponderación local.

El kernel bicuadrado define ponderaciones mediante esta fórmula:

La función de kernel depende de un ancho de banda que controla la velocidad con la que los pesos disminuyen con la distancia. El ancho de banda de cada kernel se proporciona en el parámetro Ancho de banda kernel. Para el vecindario de k vecinos más cercanos, si no se proporciona ningún valor de ancho de banda, cada entidad utilizará un ancho de banda diferente (adaptativo) igual a la distancia al vecino (k+1)º de la entidad. Para la vecindad de banda de distancia, el ancho de banda kernel se establece de forma predeterminada en el mismo valor que el parámetro Banda de distancia.

Nota:

Todas las entidades tendrán una ponderación igual a 1 para la ponderación de la entidad a sí misma, incluso si el archivo de ponderaciones espaciales no tiene estas ponderaciones asignadas. Además, las ponderaciones del vecindario de cada entidad se normalizarán para que sumen 1 (lo que se conoce como normalización de filas).

Salidas de la herramienta

La herramienta devuelve una serie de resultados que puede utilizar para investigar la asociación espacial entre las dos variables de análisis. Los resultados se devuelven como mensajes de geoprocesamiento, una clase de entidades de salida y un gráfico de dispersión.

Mensajes de geoprocesamiento

Los mensajes de geoprocesamiento devueltos por la herramienta contienen valores relacionados con la asociación espacial global entre las dos variables de análisis. En los mensajes aparecen los siguientes valores:

• L de Lee global: valor estadístico L de Lee entre las dos variables de análisis. El valor será entre -1 y 1. Los valores positivos indican una asociación espacial positiva, y los negativos, una asociación espacial negativa. Los valores cercanos a 0 indican que las variables no están asociadas espacialmente. El valor estadístico es una combinación de la correlación de los promedios de los vecindarios entre las variables de análisis y el grado de autocorrelación espacial de cada variable de análisis.
• Valor p global: valor p de una prueba bilateral de asociación espacial estadísticamente significativa. Los valores p pequeños indican que la estadística L de Lee global es estadísticamente significativa y no se debe a una variación aleatoria. Si el valor p es significativo (inferior a 0,1 para una significación del 90 %, inferior a 0,05 para una significación del 95 % e inferior a 0,01 para una significación del 99 %) y el valor estadístico L de Lee global es positivo, las dos variables de análisis están asociadas espacialmente de forma significativamente positiva. Si el valor p es significativo y el valor estadístico global L de Lee es negativo, las variables de análisis están significativamente asociadas espacialmente de forma negativa.
• Escalar de suavizado espacial (campo de análisis 1): valor entre 0 y 1 que indica el grado de autocorrelación espacial de la primera variable de análisis. Los valores cercanos a 1 indican una fuerte autocorrelación espacial positiva (los valores altos y bajos tienden a agruparse), y los valores cercanos a 0 indican una fuerte autocorrelación espacial negativa (los valores altos tienden a estar rodeados de valores bajos y viceversa).
• Escalar de suavizado espacial (campo de análisis 2): valor entre 0 y 1 que indica el grado de autocorrelación espacial de la segunda variable de análisis.
• Correlación de Pearson (sin procesar): correlación de Pearson entre las dos variables de análisis. Este valor es útil para compararlo con el valor estadístico global L de Lee para ver la diferencia entre la correlación sin procesar de las variables y su asociación espacial.
• Correlación de Pearson (promedios de vecindario): correlación de Pearson entre los promedios ponderados de los vecindarios de las dos variables de análisis. El valor estadístico L de Lee global también es aproximadamente igual a este valor multiplicado por las raíces cuadradas de los escalares de suavizado espacial.

El valor estadístico L de Lee global, el valor p global y la correlación de Pearson (sin procesar) también se devuelven como resultados derivados de la herramienta.

Clase de entidad y campos

La clase de entidad de salida contendrá los siguientes campos que resumen los resultados del valor estadístico L de Lee local:

• Copias de las dos variables de análisis y un campo del Id. de origen para cada entidad de entrada.
• Asociación espacial local (LOCAL_L): valor estadístico L de Lee local para cada entidad. Los valores superiores a 0 indican una asociación espacial positiva entre las variables de análisis en la ubicación, y los valores inferiores a 0 indican una asociación espacial negativa.
• Media ponderada de vecindad de (primera variable de análisis) (NWA_VAR1): media ponderada de vecindad de la primera variable de análisis para cada entidad. El valor es la media ponderada de los valores de la entidad y sus vecinas utilizando las ponderaciones definidas por los parámetros Tipo de vecindad, Esquema de ponderación local y Ancho de banda kernel.
• Media ponderada de vecindad de (segunda variable de análisis) (NWA_VAR2): media ponderada de vecindad de la segunda variable de análisis para cada entidad.
• Valor p (P_VALUE): valor p de una prueba de hipótesis bilateral para la significación estadística del valor estadístico L de Lee local para cada entidad.
• Nivel de significancia (SIG_LEVEL): nivel de significancia más alto alcanzado del valor estadístico L de Lee local para cada entidad. Los valores posibles son No significativo, 90 % significativo, 95 % significativo y 99 % significativo.
• Categoría de asociación espacial local (ASSOC_CAT): categoría de la asociación espacial local para cada entidad. Los valores posibles son: Not Significant, High-High, High-Low, Low-High y Low-Low. Por ejemplo, Low-High significa que la entidad es significativa al menos en un 90 por ciento, la media ponderada del vecindario de la primera variable de análisis es menor que la media de la primera variable de análisis, y la media ponderada del vecindario de la segunda variable de análisis es mayor que la media de la segunda variable de análisis.
• Número de vecinos (NUM_NBRS): número de vecinos (incluida la entidad) utilizado para calcular los valores estadísticos L de Lee local y global para cada entidad.

Gráfico de dispersión L de Lee

La capa de entidades de salida incluye un gráfico de dispersión L de Lee que muestra las medias ponderadas por vecindario de la primera variable de análisis en el eje x y las medias ponderadas por vecindario de la segunda variable de análisis en el eje y, junto con una línea de tendencia lineal ajustada a los datos. También se trazan líneas horizontales y verticales discontinuas en el valor medio de cada variable de análisis. Estas líneas dividen el diagrama de dispersión en cuatro cuadrantes y se utilizan para dividir los puntos en las categorías de asociación espacial local. Por ejemplo, las entidades estadísticamente significativas del cuadrante superior izquierdo serán de la categoría Low-High (azul claro).

El gráfico también puede utilizarse para identificar entidades individuales que se desvían de las tendencias generales del resto de entidades. Por ejemplo, puede seleccionar puntos individuales en el gráfico de dispersión que se alejen de la línea de tendencia para investigar más a fondo estas entidades. Es posible que estas entidades se agrupen en el mapa y revelen patrones regionales en las asociaciones espaciales que, de otro modo, serían difíciles de detectar.

Prácticas recomendadas y limitaciones

Plantéese lo siguiente al utilizar esta herramienta:

• Los valores atípicos (valores mucho mayores o menores que el resto de los valores) en cualquiera de las variables de análisis afectarán en gran medida a los resultados. Se recomienda crear histogramas de cada variable de análisis para determinar si hay valores atípicos y eliminar cualquier entidad que contenga valores atípicos en cualquiera de las variables. También puede utilizar ingeniería de datos para identificar valores atípicos.
• Al utilizar esta herramienta, se supone que existe una relación lineal entre las medias ponderadas por vecindario de las dos variables de análisis. Si los valores del gráfico de dispersión L de Lee muestran un patrón que no es lineal, puede utilizar la herramienta Transformar campo para aplicar transformaciones a las variables de análisis para linealizar la relación y vuelva a ejecutar la herramienta con los valores transformados.
• Un valor p estadísticamente significativo (generalmente inferior a 0,05) no significa necesariamente que exista una correlación cruzada entre las dos variables. En cambio, podría significar únicamente que una o ambas variables tienen una autocorrelación espacial elevada. Para interpretar un valor p significativo, revise los valores del valor estadístico L de Lee global, la correlación entre las medias de los vecindarios y el escalar de suavizado espacial de cada variable. Juntos, estos valores permiten interpretar el origen de la significación estadística: autocorrelación, correlación cruzada o ambas. Si el valor p es significativo, pero el valor estadístico L de Lee global y la correlación entre las medias de los barrios son muy próximos a 0 y los escalares de suavizado espacial son próximos a 1, probablemente significa que cada una de las variables está muy autocorrelacionada, pero hay poca correlación cruzada entre ellas.
• Se recomienda utilizar al menos 50 entidades de entrada e incluir al menos 8 vecinos para cada entidad.

Fórmulas

Esta sección contiene las fórmulas de todas las estadísticas calculadas por la herramienta. Para más información, consulte los artículos de la sección Referencias

En todas las fórmulas, x hace referencia a la primera variable de análisis e y hace referencia a la segunda. Una tilde (~) sobre una variable indica que se trata de una media ponderada de los valores del vecindario. Las ponderaciones de cada vecindario se normalizan para que sumen 1. Una barra sobre una variable indica que se trata de una media no ponderada de todas las n entidades de entrada. El subíndice i indica una única entidad de entrada. Todas las sumas en las fórmulas suman todas las entidades de entrada.

El valor estadístico global L de Lee se calcula con la siguiente fórmula:

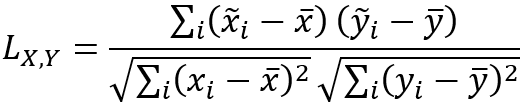
El valor estadístico L de Lee global también es aproximadamente igual al producto de las raíces cuadradas de los escalares de suavizado espacial y la correlación entre las medias ponderadas del vecindario, como se indica a continuación:

Los escalares de suavizado espacial se calculan con las siguientes fórmulas:

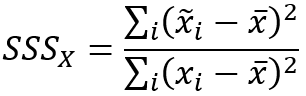
La correlación entre las medias ponderadas de los barrios se calcula con la siguiente fórmula:

La estadística local L de Lee se calcula con la siguiente fórmula:

El valor estadístico L de Lee global es igual a la media de las estadísticas L de Lee locales como se indica a continuación:

Referencias

Para implementar la herramienta, se utilizaron los siguientes recursos:

• Lee, Sang-Il. "Developing a bivariate spatial association measure: an integration of Pearson's r and Moran's I." Journal of geographical systems 3 (2001): 369-385. https://doi.org/10.1007/s101090100064.
• Lee, Sang-Il. "A generalized randomization approach to local measures of spatial association." Geographical Analysis 41.2 (2009): 221-248. https://doi.org/10.1111/j.1538-4632.2009.00749.x.