Cómo funciona el Análisis de inferencia causal

La herramienta Análisis de inferencia causal estima el efecto causal entre una variable de exposición continua y una variable de resultado continua equilibrando las variables de confusión. La herramienta utiliza la correlación de la puntuación de propensión o la ponderación inversa de la puntuación de propensión para asignar ponderaciones a cada observación, de modo que las variables de confusión queden descorrelacionadas con la variable de exposición y aislando así el efecto causal entre la exposición y el resultado. El resultado es una función exposición-respuesta (ERF) que estima cómo responde la variable de resultado a los cambios en la variable de exposición. Por ejemplo, puede estimar el aumento medio del rendimiento del maíz (resultado) para diferentes cantidades de fertilizante (exposición) y factorizar variables de confusión como el tipo de suelo, las técnicas agrícolas y las variables medioambientales que afectan a la producción de maíz. La ERF se muestra como un gráfico de dispersión y como una imagen en los mensajes de geoprocesamiento. Además, puede estimar el efecto causal de las observaciones individuales y crear objetivos basados en metas. Por ejemplo, puede calcular la cantidad de fertilizante que necesita cada explotación para producir una cantidad determinada de maíz al año.

Antecedentes del análisis de inferencia causal

El análisis de inferencia causal es un campo de la estadística que modela las relaciones de causa y efecto entre dos variables de interés. Una variable (denominada variable de exposición o tratamiento) modifica o afecta directamente a otra variable (conocida como variable de resultado). Con frecuencia, se utilizan correlaciones como medida de cómo los cambios en una variable están asociados a los cambios en la otra variable; sin embargo, la correlación no significa necesariamente que una variable cause la otra. Es posible que ambas se vean influidas por otros factores. Por ejemplo, la relación entre las ventas de helados y las de crema solar podría tener una fuerte relación positiva. Sin embargo, no se puede concluir que el aumento de las ventas de helados esté provocando un aumento de las ventas de crema solar. Deben tenerse en cuenta otros factores, como la temperatura, el índice UV o el mes del año antes de extraer conclusiones causales. Los factores que afectan tanto a las variables de exposición como a las de resultado se denominan variables de confusión y es esencial que se tengan en cuenta para captar con precisión la relación causa-efecto entre las variables de exposición y de resultado.

Un análisis causal comienza con una hipótesis basada en la investigación o en el conocimiento común. Por ejemplo, considere el efecto del ejercicio sobre la salud. Existen evidencias y un conocimiento común de que el ejercicio regular puede mejorar la salud, pero las variables también dependen de otras muchas variables de confusión como los hábitos alimentarios, las elecciones de estilo de vida y el acceso a áreas seguras para hacer ejercicio. En situaciones como esta, se puede utilizar el análisis de inferencia causal para aislar el efecto de la variable de exposición (por ejemplo, el tiempo diario dedicado al ejercicio) en la variable de resultado (por ejemplo, el resultado sanitario) después de tener en cuenta diversas variables de confusión importantes.

En los experimentos diseñados, las variables de confusión se controlan mediante ensayos aleatorios controlados (RCT, por sus siglas en inglés). Los RCT se utilizan ampliamente en la investigación clínica e implican que a los participantes se les asignan aleatoriamente diferentes niveles de exposición y se comparan sus resultados. Por ejemplo, un individuo hace ejercicio durante 10 minutos todos los días, otro durante una hora y otro no hace nada de ejercicio. Debido a que sus variables de exposición se asignaron al azar, cualquier diferencia en el resultado de salud no puede atribuirse a nada más que a la variable de exposición.

Sin embargo, en los escenarios del mundo real, con frecuencia resulta imposible o poco ético llevar a cabo experimentos controlados. Por ejemplo, para estudiar el efecto de la contaminación en la depresión, no resulta ético exponer a las personas a una contaminación elevada para ver qué ocurre con su depresión. En su lugar, solo puede observar el nivel de contaminación que ya experimentan las personas y observar sus índices de depresión. El análisis de inferencia causal puede utilizarse en estos casos para modelar la relación causal a partir de los datos observacionales, imitando un diseño experimental controlado. Para ello, se estima una puntuación de propensión para cada observación, y las puntuaciones de propensión se utilizan para estimar un conjunto de ponderaciones de equilibrio para las observaciones. Las ponderaciones de equilibrio se configuran de tal forma que mantienen la relación causal entre las variables de exposición y de resultado, pero eliminan el efecto de las variables de confusión sobre la variable de exposición, lo que permite una estimación no sesgada de la relación causal. Las observaciones ponderadas resultantes tienen propiedades análogas a las de un dataset recogido a través de un RCT, y es posible hacer inferencias a partir de él de muchas de las mismas maneras que puede hacerlo para los datasets recogidos a través de un experimento diseñado.

Dos formas habituales de estimar las ponderaciones de equilibrio son la correlación de puntuaciones de propensión y la ponderación inversa de puntuaciones de propensión. En la correlación de puntuaciones de propensión, cada observación se correlaciona con varias otras observaciones que tienen variables de confusión similares (medidas por la similitud de sus puntuaciones de propensión), pero que tienen valores de exposición diferentes. Al comparar el valor de resultado de una observación con los valores de resultado de sus correlaciones, es posible determinar cuál podría haber sido el valor de resultado de la observación si hubiera tenido exposiciones diferentes. La ponderación de equilibrio asignada a cada observación es el número de veces que se correlacionó con cualquier otra observación. En la ponderación de puntuación de propensión inversa, las ponderaciones de equilibrio se asignan invirtiendo las puntuaciones de propensión y multiplicándolas por la probabilidad global de la exposición. Este procedimiento incrementa la representación de las observaciones poco comunes (observaciones con una puntuación de propensión baja) y reduce la representación de las observaciones comunes (puntuaciones de propensión altas) para que la influencia de las variables de confusión se mantenga en proporción en todos los valores de la variable de exposición.

Las ponderaciones de equilibrio de la asignación de puntuación de propensión o de la ponderación inversa de la puntuación de propensión no siempre equilibran suficientemente las variables de confusión, por lo que sus correlaciones ponderadas se comparan con un valor de umbral. Si las correlaciones están por debajo del umbral (lo que significa que la correlación es baja), se determina que están equilibradas y se estima una ERF. Sin embargo, si las ponderaciones de equilibrio no equilibran suficientemente las variables de confusión, la herramienta devuelve un error y no genera ninguna ERF.

Aplicaciones de ejemplo

A continuación, se presentan ejemplos de aplicación de esta herramienta:

• Investigar cómo afecta la exposición a los anuncios de productos del tabaco al consumo de tabaco en los adolescentes de Estados Unidos. En este ejemplo, la variable de exposición es la cantidad de exposición a la publicidad de cada adolescente, y la variable de resultado es la cantidad de tabaco consumida por cada adolescente durante un periodo de tiempo determinado. Las variables de confusión deben ser cualquier otra variable que se conozca a ciencia cierta o se sospeche que está relacionada con la exposición o el consumo de productos del tabaco en adolescentes, como las variables socioeconómicas, la exposición directa a productos del tabaco por parte de familiares o amistades, el precio de los productos del tabaco y la disponibilidad de los productos del tabaco. Se podrían elegir muchas variables de exposición para investigar el consumo de tabaco entre los adolescentes (como la exposición directa a los productos del tabaco por parte de los miembros de la familia), pero la publicidad de los productos del tabaco es una variable de exposición útil porque, si se descubre que causa un gran aumento en el consumo de tabaco entre los adolescentes, se puede reducir la cantidad de publicidad mediante la regulación. Sin embargo, lograr una reducción en el consumo de productos del tabaco entre los miembros adultos de la familia sería más difícil de implementar como política pública.
• Estimar el efecto causal de la cantidad de fertilizante sobre el rendimiento del maíz en la agricultura de precisión, controlando al mismo tiempo el tipo de suelo, las técnicas de cultivo, las variables medioambientales y otras variables de confusión de cada parcela de cultivo. Por ejemplo, ¿cuánto aumentaría la producción de maíz si cada explotación aumentara la cantidad de fertilizante en un 10 %?
• Estimar el efecto causal entre la presión arterial y el riesgo de infarto, controlando variables de confusión como la edad, el peso, las variables sociodemográficas y el acceso a la atención sanitaria.
• En los datos espaciales, las distancias a otras entidades son con frecuencia variables de exposición útiles. Por ejemplo, la distancia a tiendas de comestibles, a zonas verdes y a hospitales provoca cambios en otras variables: una mayor distancia de las tiendas de comestibles reduce el acceso a los alimentos, una mayor distancia de un hospital reduce el acceso a la atención sanitaria, y así sucesivamente. Por razones similares, las variables espaciales y las distancias a otras entidades también suelen ser variables de confusión importantes, incluso si las variables de exposición y de resultado no son variables espaciales.

Sin embargo, el análisis de inferencia causal tiene una serie de limitaciones y supuestos que deben cumplirse para que las estimaciones de los efectos causales sean imparciales y válidas. A continuación, se exponen algunos de los supuestos y limitaciones del análisis de inferencia causal:

• Deben incluirse todas las variables de confusión importantes. Se trata de un sólido supuesto del análisis de inferencia causal y significa que si no se incluye como variable de confusión cualquier variable que esté relacionada tanto con la variable de exposición como con la variable de resultado, la estimación del efecto causal estará sesgada (una mezcla del efecto causal y el efecto de confusión de cualquier variable de confusión que falte). La herramienta no puede determinar si se han incluido todas las variables de confusión importantes, por lo que es fundamental que sopese qué variables de confusión incluye. Si hay variables de confusión importantes que no están disponibles, interprete los resultados con mucha cautela o no utilice la herramienta.
• Las correlaciones entre las variables de confusión y la variable de exposición deben eliminarse para aislar el efecto causal. En el análisis de inferencia causal, la eliminación de las correlaciones entre las variables de confusión y exposición se denomina equilibrio, y la herramienta utiliza varios procedimientos de equilibrio. Sin embargo, no siempre puede eliminar suficientemente las correlaciones entre las variables de confusión y exposición. Si el procedimiento de equilibrio no equilibra suficientemente las variables de confusión, la herramienta devolverá un error y no estimará una ERF. Consulte Consejos para lograr el equilibrio de las variables de confusión para obtener más información sobre el error y cómo resolverlo.
• La ERF no puede extrapolarse fuera del rango de valores de exposición que se utilizaron para estimarla. Por ejemplo, si la variable de exposición es la temperatura media anual, no podrá estimar nuevos resultados para temperaturas superiores a las de la muestra. Esto significa, por ejemplo, que es posible que no pueda predecir resultados en el futuro cuando las temperaturas medias superen a las actuales. Además, la herramienta recorta de forma predeterminada (elimina del análisis) el 1 % superior e inferior de los valores de exposición, por lo que el rango de la ERF será más estrecho que incluso los valores de exposición de las observaciones de la muestra.

Salidas de la herramienta

La herramienta crea una variedad de resultados que puede utilizar para investigar la relación causal entre las variables de exposición y de resultado. Los resultados se devuelven como una capa de gráficos, mensajes de geoprocesamiento, entidades de salida (o tabla) y una tabla de ERF de salida.

Función exposición-respuesta

El resultado principal de la herramienta es la ERF que estima cómo responde la variable de resultado a los cambios en la variable de exposición. La ERF calcula la nueva media poblacional (la media de todos los miembros de la población) de la variable de resultado si todos los miembros de la población cambiaran para tener el mismo valor de variable de exposición, pero mantuvieran todas sus variables de confusión existentes. Por ejemplo, en el caso de todos los condados de EE. UU., si la variable de exposición son las PM2,5 y la variable de resultado son las tasas de hospitalización por asma, la ERF calcula cómo cambiaría la tasa media nacional de hospitalización por asma si se aumentara o disminuyera el nivel nacional de PM2,5, pero manteniendo todas las demás variables (como las sociodemográficas) igual que antes del cambio en las PM2,5.

Cuando se ejecuta en un mapa activo, se incluirá un gráfico de dispersión con las entidades de salida que muestran la ERF. En los mensajes también aparece una imagen de la ERF.

La ERF estima el valor medio de la variable de resultado (eje y) si todos los miembros de la población cambiasen para tener el mismo valor de exposición (eje x).

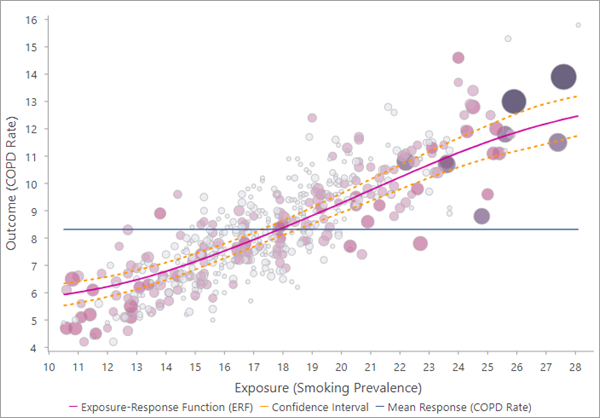
La curva rosa es la ERF entre las variables de exposición (eje x) y de resultado (eje y). Las observaciones se muestran como puntos en el diagrama de dispersión, y los puntos más grandes indican que la entidad tenía una mayor ponderación de equilibrio y contribuía en mayor medida a la estimación de la ERF. Para la correlación de puntuación de propensión, si la observación no tiene coincidencias, se dibuja como un punto gris claro. Las observaciones recortadas no aparecen en el gráfico.

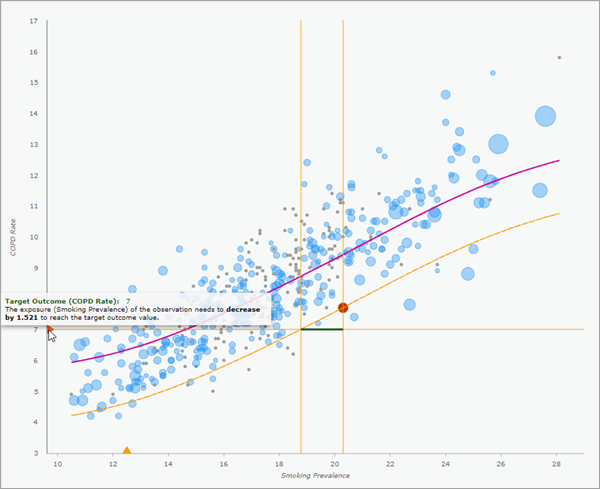
La ERF también contiene una línea horizontal azul que muestra el valor medio de la variable de resultado a modo de comparación con la media estimada para varios niveles de la variable de exposición. Por ejemplo, en la imagen que aparece a continuación, si todos los condados cambiaran su prevalencia de tabaquismo al mismo valor por debajo de aproximadamente 18 (donde la línea media cruza la ERF), la tasa global de EPOC disminuiría con respecto al nivel actual. Del mismo modo, la tasa global de EPOC aumentaría si todos los países cambiaran a una prevalencia de tabaquismo superior a 18.

También puede utilizar el parámetro Tabla de salida de la función exposición-respuesta para crear una tabla de la ERF. Si se crea, la tabla contendrá 200 valores de exposición distribuidos uniformemente entre la exposición mínima y la máxima, además del valor de respuesta (salida) correspondiente. Si se proporciona algún valor objetivo de exposición o de resultado, también se incorporará al final de la tabla junto con el valor estimado de exposición o de respuesta.

Estadísticas de equilibrio de variables de confusión

La sección Resultados de equilibrio de los mensajes muestra las correlaciones absolutas originales y ponderadas entre cada variable de confusión y la variable de exposición. Le permite ver si las ponderaciones de equilibrio redujeron efectivamente la correlación original entre las variables de confusión y la variable de exposición. Si las ponderaciones son eficaces en cuanto al equilibrio, las correlaciones ponderadas deberían ser inferiores a las correlaciones originales. La última fila de la tabla de mensajes muestra la correlación media, mediana o máxima absoluta, en función del valor del parámetro Tipo de equilibrio.

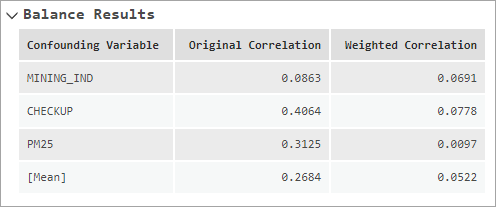
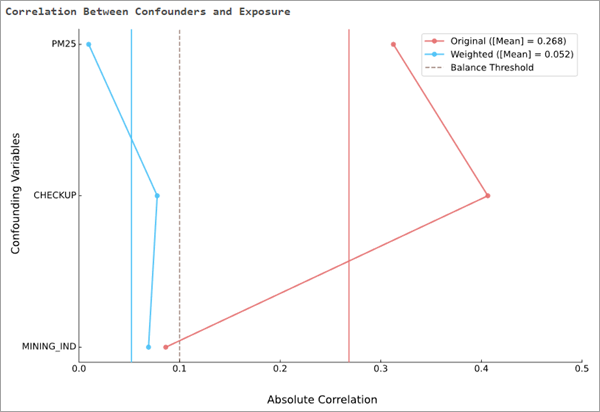
La tabla de mensajes Correlación entre variables de confusión y exposición muestra la misma información que la tabla, si bien en un gráfico de líneas verticales. Para cada variable de confusión, las correlaciones originales aparecen conectadas por una línea roja; las correlaciones ponderadas, por una línea azul. Las correlaciones agregadas originales y ponderadas también se dibujan como barras verticales rojas y azules, respectivamente. Si las ponderaciones equilibran eficazmente las variables de confusión, las líneas azules deberían estar generalmente a la izquierda de las líneas rojas. El umbral de equilibrio se dibuja como una línea discontinua vertical, lo que permite ver lo cerca que estaban las correlaciones del umbral. Por ejemplo, en la imagen que aparece a continuación, dos de las variables de confusión empezaron con correlaciones relativamente grandes (superiores a 0,3 y 0,4, respectivamente), pero las ponderaciones de equilibrio redujeron las correlaciones a menos de 0,1. La tercera variable de confusión partía de una correlación baja (ligeramente inferior a 0,1), pero las ponderaciones de equilibrio redujeron la correlación en una pequeña cantidad. En general, la correlación media se redujo de casi 0,27 a menos de 0,05.

Para más información sobre el equilibrio de las variables de confusión, consulte la sección Comprobar el equilibrio de las variables de confusión más abajo.

Resultados del ajuste de parámetros

Los mensajes también contienen secciones que resumen varios parámetros de ajuste que se utilizan para estimar la ERF. En función de los parámetros especificados en la herramienta, pueden aparecer las siguientes secciones:

• Resultados de recorte: se muestra el número original de observaciones (tras eliminar los registros con valores nulos), el número de observaciones que se eliminaron por recorte de exposición, el número de observaciones eliminadas por recorte de puntuación de propensión y el número final de observaciones que quedan tras el recorte.
• Resultados de búsqueda de cuadrícula coincidentes: para la correlación de puntuación de propensión, se muestran los resultados de la búsqueda de parámetros de correlación. La herramienta utiliza varias combinaciones de número de bin de exposición y ponderación relativa de la puntuación de propensión a la exposición (escala) y mostrará las correlaciones ponderadas resultantes para cada combinación. La combinación que resulta en la correlación ponderada más baja (mejor equilibrio) se resalta en negrita.
• Transformación que equilibra los resultados: para el modelo de puntuación de propensión de regresión, se muestran las transformaciones de las variables de confusión que se utilizaron para intentar encontrar el equilibrio, junto con la correlación ponderada para cada combinación de transformación. La combinación de transformaciones que da lugar a la correlación ponderada más baja aparece resaltada en negrita.
• Resultados de equilibrio de incremento de gradiente: para el modelo de puntuación de propensión del incremento de gradiente, se muestran los resultados de la búsqueda en cuadrícula del incremento de gradiente. Esta herramienta prueba nueve combinaciones de número de árboles y tasa de aprendizaje y muestra las correlaciones ponderadas de cada combinación. La combinación que da como resultado la correlación ponderada más baja aparece resaltada en negrita.
• Parámetros que resultan en el mejor equilibrio: para la correlación de la puntuación de propensión, se muestra el número de bins de exposición y la ponderación relativa de la puntuación de propensión a la exposición (escala) que resultaron en el mejor equilibrio de la variable de confusión. Para el incremento de gradiente, se muestran el número de árboles, la tasa de aprendizaje y el valor inicial del generador de números aleatorios que dieron como resultado el mejor equilibrio.
• Resultados de equilibrio: se muestran las correlaciones originales y ponderadas de cada variable de confusión, junto con las correlaciones media, mediana o máxima. Si se utilizaron transformaciones, también se muestra la transformación para cada variable de confusión.

Consulte la sección Estimar los parámetros óptimos de equilibrio más abajo para obtener más información sobre cómo se determinan muchos de los valores de los mensajes.

Entidades de salida

Las entidades de salida o la tabla contienen copias de las variables de exposición, resultado y confusión, junto con las puntuaciones de propensión, las ponderaciones de equilibrio (recuentos de coincidencias o ponderaciones inversas de las puntuaciones de propensión) y un campo que indica si el registro se recortó. Cuando se agregan a un mapa, las entidades de salida se dibujan en función de la ponderación de equilibrio. De esta forma, es posible comprobar si existe en las ponderaciones algún patrón espacial que pueda indicar que ciertas regiones están siendo sobrerrepresentadas o infrarrepresentadas en los resultados.

Si proporciona algún valor de exposición objetivo o de resultado, cada valor proporcionado creará dos campos adicionales en la salida. Para los valores de exposición objetivo, el primer campo contiene el valor de resultado estimado si la observación recibió la exposición objetivo; el segundo campo, el cambio estimado en la variable de resultado. Los valores positivos indican que la variable de resultado aumentará y los negativos que se reducirá. Para los valores de resultado objetivo, el primer campo contiene el valor de exposición que daría lugar al resultado objetivo, y el segundo campo contiene el cambio requerido en la variable de exposición para producir el resultado objetivo.

Si crea gráficos emergentes de la ERF local, cada registro de salida mostrará la ERF local en el panel emergente. Cualquier resultado objetivo o los valores de exposición se muestran como triángulos naranjas en los ejes x e y. Puede hacer clic en los triángulos para activar o desactivar las barras horizontales o verticales y comprobar dónde cruza el valor la ERF local. Además, puede mantener el puntero sobre los triángulos para ver información sobre los cambios necesarios en la exposición o el resultado para alcanzar el objetivo. Para más información, consulte Estimar los efectos causales locales.

Para esta observación, la prevalencia del tabaquismo debe disminuir aproximadamente un 1,5 para alcanzar la tasa objetivo de EPOC del 7.

Si crea intervalos de confianza con bootstrap para la ERF, se crearán dos campos adicionales que contienen el número de veces que se seleccionó la observación en una muestra bootstrap y el número de veces que se incluyó la observación en una muestra de bootstrap que alcanzó el equilibrio. Se recomienda buscar patrones espaciales en ambos campos. Si hay ciertas regiones que contienen muchas más muestras de bootstrap equilibradas que otras, los intervalos de confianza pueden estar sesgados (lo que suele dar lugar a intervalos de confianza poco realistas). Consulte Intervalos de confianza con bootstrap para obtener más información.

Puntuaciones de propensión

Un componente fundamental del análisis de inferencia causal es la puntuación de propensión. La puntuación de propensión se define como la probabilidad de que una observación tome su valor de exposición observado, dados los valores de sus variables de confusión. Una puntuación de propensión grande significa que el valor de exposición de la observación es común para los individuos con variables de confusión similares, mientras que una puntuación de propensión baja significa que el valor de exposición es poco común para los individuos con variables de confusión similares. Por ejemplo, si un individuo tiene la tensión arterial alta (variable de exposición), pero no tiene factores de riesgo (variables de confusión) para la tensión arterial alta, este individuo tendría probablemente una puntuación de propensión baja porque es relativamente infrecuente tener la tensión arterial alta sin ningún factor de riesgo. Por el contrario, la hipertensión arterial de un individuo con muchos factores de riesgo tendría una puntuación de propensión mayor porque se trata de una situación más común.

Dos planteamientos del análisis de inferencia causal utilizan la puntuación de propensión: la correlación de la puntuación de propensión y la ponderación inversa de la puntuación de propensión. Cada planteamiento asigna a cada observación un conjunto de ponderaciones de equilibrio que luego se utilizan para equilibrar las variables de confusión (para más información, consulte la sección Comprobar el equilibrio de las variables de confusión más abajo).

Correlación de puntuación de propensión

La correlación de puntuación de propensión intenta equilibrar las variables de confusión correlacionando cada observación con varias observaciones que presentan variables de confusión similares pero exposiciones diferentes. Al comparar el valor del resultado de la observación con los resultados de las observaciones de correlación, se ven los resultados que podría haber tenido la observación si hubiera tenido otro nivel de exposición (pero manteniendo las mismas variables de confusión). Después de encontrar correlaciones para todas las observaciones, la ponderación de equilibrio asignada a cada observación es el número de veces que la observación coincidió con cualquier otra observación. Por ejemplo, si una observación no coincide con ninguna otra, la ponderación de equilibrio será cero; si la observación coincide con todas las demás, la ponderación de equilibrio será igual al número de observaciones.

La correlación de puntuación de propensión para variables de exposición continuas es relativamente complicada y se describe y deriva por completo en los elementos cuarto y quinto de la sección Referencias más abajo. A continuación, se presenta un breve resumen del procedimiento de correlación:

Este procedimiento divide en primer lugar las observaciones en bins espaciados a intervalos regulares en función de la variable de exposición (similar a los bins de un histograma) utilizando el valor del parámetro Número de bins de exposición. La correlación de la puntuación de propensión se realiza dentro de cada bin comparando las puntuaciones de propensión de las observaciones del bin con las puntuaciones de propensión contrafactuales de todas las demás observaciones. Las puntuaciones de propensión contrafactuales son las puntuaciones de propensión que habría tenido una observación si hubiera tenido las mismas variables de confusión, pero hubiera tenido en cambio exposiciones diferentes (en este caso, los valores centrales de cada bin de exposición). Las correlaciones dentro de cada bin se determinan encontrando la observación del bin de exposición cuya puntuación de propensión se aproxime más a las puntuaciones de propensión contrafactuales de cada una de las demás observaciones. Sin embargo, dado que los valores de exposición de las observaciones contenidas en el bin no se alinearán generalmente con el centro del bin, se agrega una penalización adicional basada en la diferencia entre el valor de exposición y el centro del bin de exposición. La cantidad que se penaliza viene determinada por el valor del parámetro Ponderación relativa de puntuación de propensión a la exposición (denominado como parámetro de escala en las referencias), y la coincidencia global es la observación que presenta la suma ponderada más baja de las diferencias absolutas en las puntuaciones de propensión (puntuación de propensión menos puntuación de propensión contrafactual) y exposición (exposición bruta menos valor del centro del bin).

Ponderación inversa de la puntuación de propensión

La ponderación inversa de puntuación de propensión asigna ponderaciones de equilibrio a cada observación invirtiendo la puntuación de propensión y multiplicándola por la probabilidad global de tener la exposición dada. Este planteamiento de la inferencia causal proporciona mayores ponderaciones de equilibrio a las observaciones con puntuaciones de propensión bajas y menores ponderaciones de equilibrio a las observaciones con puntuaciones de propensión altas. El razonamiento que subyace a este esquema de ponderación es que la puntuación de propensión es una medida de lo común o poco común que es el valor de exposición para un conjunto dado de variables de confusión. Al aumentar la influencia (aumentar la ponderación de equilibrio) de las observaciones poco comunes (observaciones con puntuaciones de propensión bajas) y disminuir la influencia de las observaciones comunes, las distribuciones generales de las variables de confusión se mantienen en proporción en todos los valores de la variable de exposición.

Nota:

La estimación de la densidad kernel (KDE, por sus siglas en inglés) se utiliza para estimar la probabilidad global del valor de exposición. La KDE utiliza un kernel gaussiano con el ancho de banda de Silverman, tal y como se implementa en la función scipy.stats.gaussian_kde del paquete de Python SciPy.

Estimación de la puntuación de propensión

El parámetro Método de cálculo de la puntuación de propensión le permite especificar cómo se estimarán las puntuaciones de propensión. Cada método construye un modelo que utiliza las variables de confusión como variables explicativas y la variable de exposición como variable dependiente. Existen dos métodos de cálculo de la puntuación de propensión:

• Regresión: se utiliza la regresión por mínimos cuadrados ordinarios (MCO) para estimar las puntuaciones de propensión.

  Más información sobre la regresión de OLS

• Incremento de gradiente: se utilizan árboles de regresión con incremento de gradiente para estimar las puntuaciones de propensión.

  Más información sobre el incremento de gradiente

Para el modelo de regresión, se asignan probabilidades a las predicciones suponiendo que los residuales estandarizados se distribuyen normalmente. El modelo de incremento de gradiente no produce de forma natural residuales estandarizados, por lo que la herramienta construye un segundo modelo de incremento de gradiente para predecir el valor absoluto de los residuales del primer modelo, lo que proporciona una estimación del error estándar. A continuación, se utiliza la KDE (la misma que en la ponderación inversa de puntuación de propensión anterior) con los residuales estandarizados para crear una distribución de residuales estandarizados. Esta distribución puede utilizarse entonces para estimar puntuaciones de propensión para todas las combinaciones de valores de las variables de exposición y de confusión.

Tanto la regresión como el incremento de gradiente reescalan todas las variables para que estén entre 0 y 1 antes de construir sus respectivos modelos.

Comprobar el equilibrio de las variables de confusión

Para que la ERF sea una estimación no sesgada del efecto causal, todas las variables de confusión deben estar incluidas y equilibradas, lo que significa que las variables de confusión no deben estar correlacionadas con la variable de exposición. Dado que las variables de confusión están correlacionadas con la variable de exposición por definición, las variables de confusión originales siempre estarán desequilibradas. Sin embargo, el propósito de las ponderaciones de equilibrio (de los recuentos de coincidencia de la puntuación de propensión o de las ponderaciones inversas de la puntuación de propensión) es ponderar cada observación de forma que las observaciones ponderadas estén equilibradas, pero manteniendo la relación causal entre las variables de exposición y de resultado, lo que permite una estimación no sesgada de la ERF.

Para determinar si las ponderaciones de equilibrio equilibran eficazmente las variables de confusión, se calculan las correlaciones ponderadas entre cada variable de confusión y la variable de exposición. A continuación, se agregan los valores absolutos de las correlaciones ponderadas y se comparan con un valor de umbral. Si la correlación agregada es inferior al umbral, se determina que las variables de confusión están equilibradas. Puede especificar el tipo de agregación (media, mediana o correlación absoluta máxima) mediante el parámetro Tipo de equilibrio y proporcionar el valor umbral en el parámetro Umbral de equilibrio. De forma predeterminada, la herramienta calcula la correlación media absoluta y utiliza un valor de umbral igual a 0,1.

Nota:

Para las variables de confusión continuas, las correlaciones ponderadas se calculan utilizando un coeficiente de correlación de clasificación de Spearman ponderado. Esta correlación es similar a un coeficiente de correlación de Pearson tradicional, pero utiliza los rangos ponderados de las variables en lugar de valores brutos. El uso de rangos hace que la correlación sea más robusta frente a los valores atípicos y distribuciones con formas extrañas. En el caso de las variables de confusión de categorías, las correlaciones ponderadas se calculan mediante una estadística eta ponderada que utiliza rangos ponderados de la variable de exposición. La estadística eta es un equivalente cercano de la correlación absoluta de Pearson para las variables de categorías ambas pueden definirse como la raíz cuadrada de R cuadrado, el coeficiente de determinación, y el uso de rangos ponderados en lugar de valores de exposición brutos la convierte en un equivalente cercano del valor absoluto de una correlación ponderada de Spearman.

Consejos para lograr el equilibrio de las variables de confusión

Si las ponderaciones de equilibrio no equilibran suficientemente las variables de confusión, la herramienta devolverá un error y no producirá una ERF; sin embargo, se siguen mostrando varios mensajes con información sobre las correlaciones ponderadas de cada variable de confusión. Cuando se encuentre con este error, consulte los mensajes para determinar en qué medida las ponderaciones de equilibrio redujeron las correlaciones y lo cerca que estaba la correlación ponderada del umbral de equilibrio.

Cuando la herramienta no logre el equilibrio, considere si le falta alguna variable de confusión relevante e incluya las que le falten. A continuación, pruebe con otro tipo de opciones para los parámetros Método de cálculo de la puntuación de propensión y Método de equilibrio. Sin embargo, para algunos datasets, puede que no haya ninguna combinación que logre el equilibrio.

En general, cuanto mayores sean las correlaciones originales de las variables de confusión, más difícil será equilibrarlas. En el caso de variables de confusión fuertemente correlacionadas, puede ser necesario un gran tamaño de la muestra para lograr un equilibrio suficiente. En el caso de las variables de confusión categóricas, cuantas más categorías haya, más difícil es lograr el equilibrio. Puede ser necesario combinar algunas de las categorías, especialmente si hay poca variación de la variable de exposición o un número reducido de observaciones (generalmente menos de cinco) en cada categoría.

Sin embargo, si puede tolerar la introducción de sesgos en la ERF, puede lograr el equilibrio aumentando el umbral de equilibrio o utilizando un tipo de equilibrio más permisivo.

En general, un valor de umbral de equilibrio más bajo indica menos tolerancia al sesgo en la estimación del efecto causal; sin embargo, es más difícil lograr el equilibrio cuando se usan umbrales más bajos. Para el tipo de equilibrio, el uso del valor medio de las correlaciones garantiza que las variables de confusión estén equilibradas por término medio, pero sigue existiendo el riesgo de que algunas variables de confusión tengan correlaciones grandes si hay un número suficiente de ellas con correlaciones más bajas como para que la media esté por debajo del umbral. La opción máxima es la más conservadora y requiere que cada variable de confusión esté por debajo del umbral; sin embargo, si incluso una sola variable de confusión está ligeramente por encima del umbral, las variables de confusión se considerarán desequilibradas. La opción de mediana es la más indulgente, y permite que hasta la mitad de las correlaciones sean muy grandes y aún así se consideren equilibradas.

Estimar los parámetros óptimos de equilibrio

Con frecuencia, conseguir el equilibrio de las variables de confusión puede resultar difícil, por lo que la herramienta prueba con varias optimizaciones y búsquedas para encontrar parámetros de ajuste que den como resultado variables de confusión lo más equilibradas posible. Las optimizaciones que se realicen dependen de varios parámetros de la herramienta y se describen en las secciones siguientes.

Búsqueda de parámetros de correlación

En la correlación de puntuaciones de propensión, los resultados de la correlación dependen de los valores de los parámetros Número de bins de exposición y Ponderación relativa de puntuación de propensión a la exposición, pero resulta difícil predecir los valores que darán lugar al mejor equilibrio. Además, cualquier mínimo cambio en cualquiera de los valores puede provocar grandes cambios en el otro, por lo que resulta particularmente complicado encontrar un par de valores que funcione eficazmente. Si no se proporcionan valores para los parámetros, la herramienta probará con varias combinaciones y mostrará los resultados en forma de tabla en los mensajes. En la tabla, las filas son el número de bins de exposición y las columnas son las ponderaciones relativas (a menudo denominadas como escala). La correlación ponderada de cada combinación se muestra en la cuadrícula, y cualquier combinación que haya alcanzado el equilibrio tendrá un asterisco junto al valor. La combinación que resulta en la correlación ponderada más baja (mejor equilibrio) se resalta en negrita. Como se muestra en la imagen que aparece a continuación, las correlaciones ponderadas pueden variar sustancialmente para distintos valores de los dos parámetros.

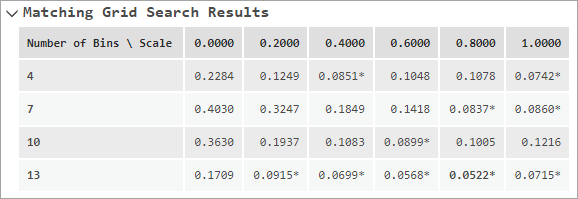
Esta herramienta intenta ponderaciones relativas que van de 0 a 1 por 0,2, pero el número de bins de exposición que se prueban depende del número de observaciones. Los valores probados oscilan entre la raíz cuarta y dos veces la raíz cúbica del número de observaciones. Los valores probados se incrementarán uniformemente en no menos de tres, y no se probarán más de 10 valores.

Transformaciones de regresión

Al utilizar la regresión para calcular las puntuaciones de propensión, si las variables de confusión no están equilibradas, se aplican diversas transformaciones a cualquier variable de confusión continua. Si en algún momento las variables de confusión alcanzan el equilibrio, el proceso finaliza y el conjunto actual de transformaciones se utiliza para construir la ERF.

El proceso comienza con la variable de confusión menos equilibrada (mayor correlación ponderada) y aplica una secuencia de transformaciones. Se conserva la transformación que logre el mejor equilibrio y el proceso se repite con la siguiente variable de confusión. El proceso continúa hasta que todas las variables de confusión se han probado con todas las transformaciones, y si las variables de confusión siguen sin estar equilibradas, la herramienta devuelve un error y no genera ninguna ERF.

Se realizarán las siguientes transformaciones, con algunas restricciones sobre los valores de las variables de confusión que se transforman:

• Logaritmo natural: solo para variables de confusión con valores positivos
• Cuadrado: solo para variables de confusión con valores no negativos
• Raíz cuadrada: solo para variables de confusión que presentan valores no negativos
• Cubo
• Raíz cúbica

Las transformaciones que dieron como resultado el mejor equilibrio se muestran en la sección Resultados de equilibrio de los mensajes, y el historial completo de los intentos de transformación se muestra en la sección Transformación que equilibra los resultados.

En la correlación de puntuación de propensión, se utiliza el número de bins de exposición y los valores de ponderación relativa de las variables de confusión originales (sin transformar) para todas las combinaciones de transformación. Así se evitan los tiempos de cálculo excesivamente largos al repetir la búsqueda de parámetros de correlación para cada combinación de transformación. La transformación de cuadrado se restringe a valores no negativos para que el orden de los valores de las variables de confusión no cambie antes y después de la transformación, lo que es importante a la hora de reutilizar el número de bins de exposición y la ponderación relativa determinados a partir de las observaciones originales.

Búsqueda de parámetros con incremento de gradiente

Cuando se utiliza el incremento de gradiente para calcular puntuaciones de propensión, se prueban varias combinaciones del número de árboles y de la tasa de aprendizaje. Si en algún momento las variables de confusión alcanzan el equilibrio, el proceso finaliza y se utilizan el número de árboles y la tasa de aprendizaje actuales. El proceso prueba hasta nueve combinaciones: número de árboles igual a 10, 20 y 30 árboles y tasas de aprendizaje iguales a 0,1, 0,2 y 0,3.

El número de árboles y la tasa de aprendizaje que dan como resultado el mejor equilibrio se mostrarán en la sección Parámetros que resultan en el mejor equilibrio de los mensajes, y el historial completo de combinaciones de parámetros se mostrará en la sección Resultados de equilibrio de incremento de gradiente.

A diferencia de las transformaciones de regresión, la búsqueda de parámetros de correlación para el número de bins de exposición y la ponderación relativa se repite con cada combinación de número de árboles y tasa de aprendizaje. Se realiza una búsqueda más profunda porque cualquier mínimo cambio en cualquiera de estos cuatro parámetros puede provocar cambios considerables en los valores óptimos de los demás.

Estimar la función exposición-respuesta

El procedimiento de ponderación de equilibrio asigna ponderaciones de equilibrio (recuentos de coincidencias o ponderaciones inversas de puntuación de propensión) a cada observación, y estas ponderaciones son la base para estimar la función de exposición-respuesta. Cada una de las observaciones ponderadas (a veces denominadas como seudopoblación) tiene un valor de exposición, un valor de resultado y una ponderación, y el objetivo es ajustar una curva suave (la ERF) a las observaciones ponderadas. Al estimar la ERF, cada observación influye en la estimación proporcionalmente a su ponderación. En otras palabras, una observación que presenta una ponderación igual a tres contribuye tanto como tres observaciones con una ponderación igual a uno cada una. Del mismo modo, aquellas observaciones que presentan una ponderación igual a cero no tienen ningún impacto en la ERF, lo que provoca de hecho la exclusión de la observación.

Para un valor determinado de la variable de exposición (eje x), el valor de respuesta asociado (eje y) se estima como una media móvil ponderada (a veces denominada suavizador kernel) de los valores resultantes de las observaciones. Las ponderaciones de la media ponderada son las ponderaciones de equilibrio multiplicadas por la ponderación de un kernel gaussiano recortado en tres desviaciones estándar.

Si este procedimiento se realiza en todos los valores de la variable de exposición, el resultado es una curva suave que pasa por las observaciones y se dirige hacia las observaciones con mayor ponderación.

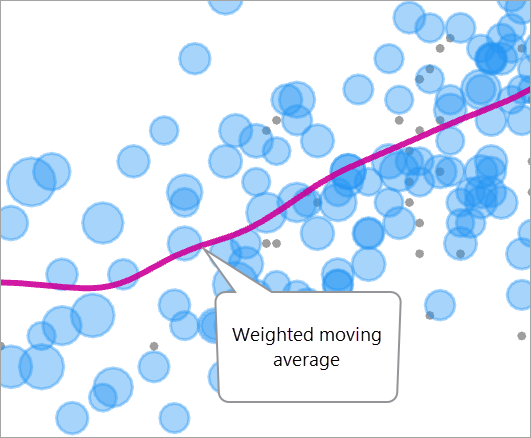
Estimación del ancho de banda

El kernel de la fórmula de la ERF depende de un valor de ancho de banda (la desviación estándar del kernel gaussiano) que controla la suavidad de la curva de la ERF, y especificar un ancho de banda apropiado es fundamental para producir una ERF realista y precisa. Los valores de ancho de banda mayores dan lugar a ERF más suaves para el mismo conjunto de observaciones ponderadas. La siguiente imagen muestra tres valores de ancho de banda utilizados para las mismas observaciones:

Puede utilizar el parámetro Método de estimación del ancho de banda para elegir cómo estimar un valor de ancho de banda. Existen tres métodos de estimación del ancho de banda:

• Plug-in: se utiliza una fórmula rápida de regla general para estimar el valor del ancho de banda. Esta opción es la predeterminada, se calcula rápidamente y, en general, produce ERF precisas y realistas. El método es una variante ponderada de la metodología de Fan (1996) y deriva el valor del ancho de banda de la segunda derivada de un polinomio global ponderado de cuarto orden ajustado a todas las observaciones.
• Validación cruzada: se utiliza el valor de ancho de banda que minimiza el error cuadrático medio de validación cruzada. Esta opción es la que tarda más en calcularse, pero es la más fundamentada en la teoría estadística. Sin embargo, para los datasets grandes, la validación cruzada tiene tendencia a estimar valores de ancho de banda demasiado pequeños y a producir ERF demasiado curvas.
• Manual: se utiliza el valor de ancho de banda personalizado proporcionado en el parámetro Ancho de banda. Esta opción se recomienda cuando las otras opciones generan valores de ancho de banda que dan lugar a ERF demasiado suaves o demasiado curvas. En este caso, consulte los valores del ancho de banda estimados por los otros métodos y haga las correcciones necesarias para ajustar la suavidad.

El valor estimado del ancho de banda se indica en la parte inferior de los mensajes.

Nota:

Para los métodos plug-in y de validación cruzada, si el valor estimado del ancho de banda es inferior a la mayor diferencia entre los valores de exposición, se estimará en su lugar la mayor diferencia. Así se garantiza que cada valor de exposición tenga datos suficientes para la media ponderada. Para utilizar valores de ancho de banda menores, proporcione un valor de ancho de banda manual.

Estimar los efectos causales locales

Puede crear ERF locales para cada registro de la función o tabla de salida activando el parámetro Habilitar ventanas emergentes con una función de exposición-respuesta. Si se activa, la salida contiene un gráfico ERF en las ventanas emergentes de cada registro de entidad o tabla de salida. Las ventanas emergentes muestran en qué medida se estima que la variable de resultado de la observación individual responde a los cambios en su variable de exposición. La ERF local adopta la misma forma que la ERF global, pero se desplaza hacia arriba o hacia abajo para pasar por la observación individual. Además, si se proporciona algún resultado objetivo o valores de exposición, estos resultados se muestran en los gráficos emergentes junto con los cambios necesarios en la exposición o el resultado para alcanzar los objetivos.

La creación de ERF locales o el uso de valores objetivo de exposición o de resultados requiere hacer una suposición adicional de un efecto de exposición fijo para todas las observaciones. Se trata de una suposición fuerte, y violarla puede conducir a resultados sesgados o engañosos. La hipótesis del efecto fijo de la exposición implica que el efecto de la exposición sobre el resultado es constante en todos los individuos de la población. En otras palabras, dada su exposición inicial, el aumento de la exposición en una cantidad fija cambia el resultado de la misma manera para todos, independientemente de los niveles de cualquier otra variable (incluidos, entre otros, los factores de confusión medidos). Por ejemplo, aumentar la cantidad de fertilizante de 150 libras por acre a 175 libras por acre debería conducir a un aumento del rendimiento del maíz en la misma cantidad en todas las explotaciones, independientemente de su rendimiento actual de maíz, tipo de suelo, técnicas de cultivo u otras variables de confusión.

Esta suposición es razonable siempre y cuando no haya modificadores del efecto, es decir, variables que afecten a la forma en que el resultado responde a la exposición a nivel individual. Sin embargo, las variables sociodemográficas, entre ellos el sexo, el origen racial o los niveles educativos, son a menudo modificadores del efecto y suelen incluirse como variables de confusión en los modelos de inferencia causal. Esta posibilidad funciona a la hora de promediar la modificación del efecto en todos los niveles de la variable modificadora, lo que permite estimar un efecto causal medio global (la ERF). Sin embargo, la ERF global no representa ningún subgrupo específico definido por los niveles del modificador del efecto. Por ejemplo, un programa de formación profesional podría mostrar un aumento de las ofertas de empleo con más horas de formación. Sin embargo, en los EE. UU., las ofertas de empleo se estancan después de ciertas horas de formación en vecindarios en los que predomina la población negra o hispana, lo que podría sugerir una discriminación sistémica en la contratación. Por lo tanto, la ERF global puede enmascarar involuntariamente las disparidades a las que se enfrentan estas comunidades. La ERF global representa el efecto de la exposición sobre los resultados promediados en toda la población; sin embargo, en presencia de variables modificadoras del efecto, la ERF global podría no representar con exactitud el efecto de la exposición en los resultados en las áreas con población predominantemente negra o hispana.

Las ERF locales no son válidas cuando el modelo contiene modificadores de efectos. Un planteamiento válido a la hora de abordar los modificadores del efecto es la estratificación, que consiste en dividir las observaciones en estratos (o subgrupos) en función de los valores de la variable modificadora. Al separar los modificadores del efecto por estratos y construir ERF independientes para cada estrato, es posible examinar la relación entre la exposición y el resultado dentro de cada grupo por separado. Esta posibilidad le permite comprobar si el efecto de la exposición en el resultado difiere según los distintos niveles del modificador del efecto.

Intervalos de confianza con bootstrap

Puede crear intervalos de confianza del 95 por ciento para la ERF utilizando el parámetro Crear intervalos de confianza con bootstrap. Si se crean, los intervalos de confianza se dibujarán como líneas discontinuas por encima y por debajo de la ERF en el gráfico de dispersión y en los mensajes. Si se crea una tabla de ERF de salida, esta también contendrá campos de los límites de confianza superior e inferior.

Los intervalos de confianza del 95 % se muestran por encima y por debajo de la ERF como líneas discontinuas.

Los intervalos de confianza son límites de la media poblacional de la variable de resultado para cualquier valor dado de la variable de exposición. Dado que los promedios de la población presentan menos variabilidad que los miembros individuales de la población, la mayoría de los puntos del diagrama de dispersión no caerán generalmente dentro de los intervalos de confianza, aunque no constituye necesariamente un signo de problemas. Por razones similares, los intervalos de confianza solo son aplicables a la ERF global, y no pueden aplicarse a ninguna ERF local.

Los intervalos de confianza se crean utilizando bootstrapping M de N. Este procedimiento implica el muestreo aleatorio de M observaciones de las N observaciones, donde M=2*sqrt(N), tal y como recomienda DasGupta (2008). A continuación, la herramienta realiza todo el algoritmo (búsqueda de parámetros óptimos, estimación de la puntuación de propensión, prueba de equilibrio y estimación de la ERF) en la muestra de bootstrap aleatoria. La ERF resultante será normalmente similar a la ERF original, pero no será exactamente igual. Al repetir este proceso muchas veces, es posible comprobar cuánto varía la ERF al tomar diferentes muestras aleatorias de las observaciones. La variación de las ERF resultantes es lo que impulsa la creación de los intervalos de confianza.

Si una muestra de bootstrap no alcanza el equilibrio (según lo determinado por el tipo de equilibrio y el umbral de equilibrio), la muestra de bootstrap se descartará. La herramienta seguirá realizando bootstraps hasta que 5*sqrt(N) muestras de bootstrap alcancen el equilibrio. Este valor se obtiene de forma que se espera que cada observación se incluya en al menos 10 muestras de bootstrap equilibradas por término medio. De esta forma, es posible obtener estimaciones estables de los límites superior e inferior en todo el rango entre de exposición. Si tras de 25*sqrt(N) intentos de bootstrap sigue sin haber suficientes bootstraps equilibrados, no se crean los intervalos de confianza y se devuelve un mensaje de advertencia.

Aunque los intervalos de confianza captan muchas fuentes de incertidumbre de la ERF, es importante señalar que, para crear intervalos de confianza que correspondan realmente a límites superiores e inferiores del efecto causal, deben tenerse en cuenta todas las fuentes potenciales de incertidumbre. El procedimiento bootstrap de esta herramienta incorpora la incertidumbre del procedimiento de equilibrio y la estimación de la ERF, pero no puede dar cuenta de otras posibles fuentes de incertidumbre, como la imprecisión en los valores de las variables o la elección de la forma funcional de la ERF (una media móvil ponderada, frente a un spline o un polinomio global, por ejemplo). Además, los intervalos de confianza se volverán arbitrariamente estrechos a medida que aumente el número de observaciones, aunque no debe tomar este hecho como que la ERF es una caracterización perfecta del efecto causal.

Al crear intervalos de confianza con bootstrap, las características o tabla de salida contendrán dos campos relacionados con los bootstraps. El primer campo contiene el número de veces que se seleccionó la observación en una muestra de bootstrap; el segundo campo contiene el número de veces que se incluyó la observación en una muestra de bootstrap que alcanzó el equilibrio y se estimó una ERF. Estos campos se crearán, aunque no haya suficientes muestras de bootstrap que alcancen el equilibrio para estimar los intervalos de confianza. En el caso de las entidades de salida, los valores de la primera columna deben mostrar pocos patrones espaciales, excepto alrededor del perímetro de las entidades. Sin embargo, si existen patrones espaciales en el segundo campo, este hecho puede indicar un proceso espacial que no se está teniendo en cuenta. Por ejemplo, si la mayoría de las muestras de bootstrap equilibradas proceden de regiones concretas de los datos, estas regiones estarán sobrerrepresentadas en los intervalos de confianza y los intervalos pueden ser poco realistas. Si observa patrones espaciales en los recuentos de muestras de bootstrap equilibradas, considere la posibilidad de incluir una variable de confusión espacial (como una región geográfica) para dar cuenta del efecto espacial ausente.

Para las tablas de entrada, cada bootstrap selecciona M observaciones de forma aleatoria y uniforme. El muestreo presenta sustitución, por lo que la misma observación puede seleccionarse varias veces en el mismo bootstrap. En el caso de la entrada de entidades, las muestras de bootstrap se generan seleccionando una única entidad al azar e incluyéndola a ella y a sus ocho entidades vecinas más cercanas en la muestra. Esta selección aleatoria se repite con reemplazo hasta que se incluyen al menos M observaciones en la muestra de bootstrap. Las mismas entidades pueden resultar seleccionadas aleatoriamente varias veces e incluirse como vecinas varias veces. El uso de vecindarios aleatorios en lugar de una selección completamente aleatoria ayuda a corregir los factores de confusión espaciales no medidos (aunque aún se le anima a corregir los factores de confusión espaciales incluyendo variables espaciales como variables de confusión).

Dado que las ERF no pueden expandirse más allá del rango de valores de exposición utilizados para construirlas, la ERF de cada muestra de bootstrap solo se crea entre la exposición mínima y máxima de las observaciones de la muestra aleatoria. Con frecuencia, supone que ni los valores de exposición más altos ni los más bajos estarán dentro del rango de los valores muestreados aleatoriamente, por lo que se crean menos ERF con bootstrapping para los valores de exposición más extremos.

Una vez completados todos los bootstraps, se crean los intervalos de confianza del 95 % suponiendo una distribución en T de los valores de la ERF con bootstrap para cada valor de exposición. La varianza de los valores de la ERF se reescala multiplicándola por (M/N) para ajustarla al muestreo solo de M valores, y el grado de libertad es el número de ERF con bootstrapping que podrían generarse para el valor de exposición, menos uno. Además, las anchuras de los intervalos de confianza se suavizan utilizando el mismo suavizador de kernel que se utilizó para estimar la ERF original (ponderaciones iguales con ancho de banda de plug-in). A continuación, la anchura suavizada se suma y se resta de la ERF original para obtener los límites de confianza superior e inferior. Si se crea una tabla de ERF de salida, contendrá campos con la desviación estándar suavizada (anchura suavizada dividida por el valor crítico) y el número de ERF con bootstrap que podrían generarse para el valor de exposición.

Referencias

Para implementar la herramienta, se utilizaron los siguientes recursos:

• DasGupta, Anirban. 2008. "Asymptotic Theory of Statistics and Probability." New York, NY. Springer. ISBN 978-0-387-75971-5. https://doi.org/10.1007/978-0-387-75971-5.

• Fan, Jianquin. 1996. "Local Polynomial Modeling and Its Applications: Monographs on Statistics and Applied Probability 66." (1st ed.). Routledge. https://doi.org/10.1201/9780203748725.

• Imbens, Guido y Donald B. Rubin. 2015. "Causal Inference for Statistics, Social, and Biomedical Sciences: An Introduction." Cambridge: Cambridge University Press. https://doi.org/10.1017/CBO9781139025751.

• Khoshnevis, Naeem, Xiao Wu y Danielle Braun. 2023. "CausalGPS: Matching on Generalized Propensity Scores with Continuous Exposures." R package version 0.4.0. https://CRAN.R-project.org/package=CausalGPS.

• Wu, Xiao, Fabrizia Mealli, Marianthi-Anna Kioumourtzoglou, Francesca Dominici y Danielle Braun. 2022. "Matching on Generalized Propensity Scores with Continuous Exposures." Journal of the American Statistical Association. https://doi.org/10.1080/01621459.2022.2144737.