Cómo funciona Calcular índices

La herramienta Calcular índices calcula una serie de índices. Puede utilizar la herramienta para calcular porcentajes, índices, índices de incidencia e índices suavizados. Los índices suavizados pueden calcularse mediante el uso de los métodos de índice Bayes empírico global, índice Bayes empírico local, promedio ponderado localmente o mediana ponderada localmente.

El método de índice bruto puede utilizarse para calcular porcentajes, índices e índices de incidencia. Sin embargo, si las entidades tienen un recuento o una población reducidos, un método de suavizado resulta más adecuado. Los métodos de suavizado utilizan información de los vecinos espaciales de una entidad o de un índice de referencia para ajustar el índice bruto de cada entidad. La herramienta incluye los siguientes métodos de suavizado:

• Bayes empírico global: ajusta el índice bruto de cada entidad para que se acerque al índice de referencia global. El tamaño de población de la entidad afecta al grado del ajuste. Utilice esta opción si cree que existe un riesgo subyacente constante en todas las entidades.
• Bayes empírico local: ajusta el índice bruto de cada entidad para que se acerque al índice de referencia local. Utilice esta opción si cree que existe variabilidad espacial en el riesgo.
• Promedio ponderado localmente: determina el índice de cada entidad mediante el uso del índice promedio ponderado de su vecindad.
• Mediana ponderada localmente: determina el índice de cada entidad mediante el uso del índice medio ponderado de su vecindad.

Potenciales aplicaciones

Los índices se calculan en las siguientes situaciones:

• Calcular porcentajes simples. Por ejemplo, el porcentaje de personas en edad laboral que están desempleadas.
• Calcular relaciones. Por ejemplo, la proporción de mujeres y hombres de cada condado.
• Calcular índices de incidencia. Por ejemplo, los índices de cáncer de esófago en mujeres. Este índice es una estimación de la probabilidad de observar un evento por individuo en la población durante un período determinado. Representa la probabilidad de que el evento ocurra durante ese período para un individuo seleccionado al azar de esa población. En este escenario, el índice es un número entre 0 y 1, y los recuentos son un subconjunto de los individuos de la población.
• Para medir la intensidad de la ocurrencia de un evento en relación con una unidad de referencia. Por ejemplo, la intensidad de los tweets publicados por individuo durante 2020. En este caso, el índice puede exceder uno porque los recuentos no son necesariamente un subconjunto de la población.

Conceptos de fondo

La herramienta Calcular índices puede calcular un índice mediante uno de los siguientes métodos: Índice bruto, Bayes empírico global, Bayes empírico local, Promedio ponderado localmente o Mediana ponderada localmente. El índice bruto es el método más simple y calcula la relación entre los recuentos de un evento y la población durante un período específico.

Por ejemplo, para entender las tasas de mortalidad infantil, puede empezar el análisis utilizando el método de índice bruto con el fin de calcular una tasa simple. El gráfico siguiente muestra la tasa de mortalidad infantil en 728 entidades espaciales dividiendo el número de muertes infantiles en 2020 por el número total de niños nacidos en 2020. Los datos incluyen algunas ciudades grandes intercaladas con numerosos pueblos pequeños. Existe una varianza considerable en el tamaño de la población y en el número de niños, en las entidades espaciales.

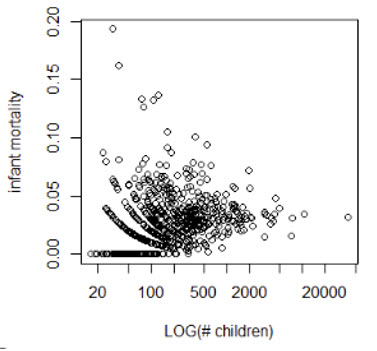
El gráfico se caracteriza por una variabilidad significativa en los índices cuando el número de niños nacidos es pequeño y una variabilidad relativamente pequeña cuando el número de niños nacidos es grande. Para áreas con menos de 100 nacimientos en un año, los índices varían desde 0 (el valor más bajo posible) hasta 0,20. Un índice de mortalidad infantil estimado del 0,20 o de 2 de cada 10 niños nacidos no se observa ni siquiera en las regiones empobrecidas del mundo. En cambio, no hay tasas inferiores al 0,02 ni superiores al 0,08 en zonas con al menos 1.000 nacimientos. Esto puede sugerir que las tasas de mortalidad infantil altas son más probables en áreas con poblaciones más pequeñas. Sin embargo, la causa principal es la mayor varianza de las tasas en áreas pequeñas, lo que da como resultado tasas menos fiables que las calculadas para regiones más pobladas.

La mayor variabilidad se debe a la extrema sensibilidad de los índices al tamaño de la población, más que a diferencias reales en las probabilidades de muerte en las áreas. Esto está relacionado con lo que se ha denominado el problema de los números bajos. Este problema tiene lugar cuando se calculan porcentajes, relaciones, proporciones o índices de áreas geográficas en las que la población está dispersa o donde el evento es excepcional. En estas situaciones, las pequeñas fluctuaciones aleatorias en el recuento de eventos puede causar grandes fluctuaciones en los valores de índice resultantes. En el ejemplo anterior, 15 áreas tuvieron menos de 30 nacimientos y no experimentaron muertes. Si ocurriera una sola muerte en estas áreas, las tasas aumentarían de 0 a un valor entre 0,05 y 0,42 (o una probabilidad de mortalidad del 42 por ciento).

Al calcular índices, le interesa comprender cómo varía la probabilidad de un evento o, en este ejemplo de mortalidad infantil, en el espacio. Sin embargo, parte de la variación de los índices brutos se debe a fluctuaciones que no están asociadas con la probabilidad subyacente del evento. Esta variación es mayor para entidades con poblaciones más pequeñas, lo que hace que sus índices sean menos fiables que las tasas calculadas para entidades con poblaciones grandes. Para superar esta limitación del método de índice bruto, puede utilizar otro método de cálculo de índices disponible en la herramienta Calcular índices.

Los métodos Bayes empírico local y Bayes empírico global abordan la variabilidad en los índices brutos de entidades con población pequeña ajustando el índice bruto de cada entidad hacia un índice de referencia. El alcance del ajuste depende del tamaño de la población: las poblaciones más grandes experimentan cambios mínimos entre su estimación de índice bruto y su estimación empírica de Bayes, y las poblaciones más pequeñas experimentan ajustes más notables.

Más información sobre Bayes empírico global

Más información sobre Bayes empírico local

Los métodos de promedio ponderado localmente, mediana ponderada localmente y Bayes empírico local aplican suavizado espacial para calcular los índices. El índice de cada entidad se calcula utilizando el índice de su vecindad. Una vez que se identifican los vecinos y las ponderaciones de los vecinos de cada entidad, los índices de entidad se calculan utilizando el parámetro Método de índice. El índice de cada entidad es uno de los siguientes:

• Promedio ponderado localmente: el índice promedio ponderado de su vecindad.

  Más información sobre el promedio ponderado localmente

• Mediana ponderada localmente: el índice medio ponderado de su vecindad.

  Más información sobre la mediana ponderada localmente

Entradas de herramienta

La herramienta incluye varios parámetros para definir y configurar los índices.

Campos de índice

El parámetro Campos de índice especifica los campos que se utilizan para calcular los índices. El parámetro incluye un valor de Campo de recuento, que especifica el campo en la capa de entrada con los recuentos de eventos, y un valor de Campo de población, que especifica el campo en la entrada con datos de población que corresponden al campo de recuento seleccionado.

Puede calcular un índice único o varios índices. Para calcular varios índices, proporcione múltiples valores de Campo de recuento y Campo de población. Por ejemplo, si la clase de entidad contiene un campo para recuentos de muertes por cáncer en 2014, 2020 y 2024 y un campo de población para esos mismos años, podría calcular tres índices de muerte por cáncer. Si calcula varios índices, se aplicarán los valores de los parámetros Método de índice y Multiplicador de índice especificados para calcular cada índice.

Método de índice

El parámetro Método de índice especifica el método utilizado para calcular los índices.

índice bruto

La estimación del índice bruto se calcula de la siguiente manera:

Donde r_i es el índice bruto, n_i es la población y Y_i es el recuento en la entidad espacial i^th. El índice bruto se calcula para cada entidad; sin embargo, las entidades con un recuento menor que cero o una población menor o igual a cero recibirán un índice nulo. Puede evaluar la fiabilidad de cada estimación de índice bruto utilizando los campos Confidence interval- upper 95%, Confidence interval- lower 95% y Reliable que se incluyen en la tabla o clase de entidad de salida. Si muchas entidades tienen intervalos de confianza o valores de fiabilidad grandes, considere usar un método de índice diferente.

Más información sobre los valores del intervalo de confianza

Más información sobre valores fiables

Bayes empírico global

El método de índice Bayes empírico global estima los índices tomando un promedio ponderado del índice bruto y un índice de referencia. El método se calcula de la siguiente manera:

donde i es la entidad espacial, 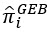es la estimación de índice Bayes empírico global, C_i es una ponderación con un valor entre 0 y 1, es la estimación de índice bruto de la entidad i, y es el índice de referencia.

El índice de referencia es el índice promedio de todas las entidades. El índice de referencia se calcula dividiendo la suma de todos los recuentos de entidades por la suma de todas las poblaciones de entidad de la siguiente manera:

donde es el índice de referencia, Y_i es la población de la entidad i^th y n_i es su recuento. La ponderación, C_i, varía entre entidades y se ve afectado por el tamaño de la población de la entidad. Si una entidad tiene una población grande, la ponderación se acerca mucho a 1 y la estimación del índice Bayes empírico global de una entidad es prácticamente idéntica a su estimación de índice bruto. Si la población es pequeña, el índice bruto se reduce hacia el índice de referencia porque la ponderación C_i, será menor que 1 y la estimación del índice Bayes empírico global será un promedio ponderado del índice bruto y el índice de referencia.

Si el parámetro Método de índice está establecido en Bayes empírico global o Bayes empírico local, también debe especificar un valor para el parámetro Distribución de probabilidad. La distribución de probabilidad es la distribución que se supone para modelar los valores de recuento observados. El parámetro Distribución de probabilidad incluye dos opciones: Poisson y Binomial. La opción predeterminada es Poisson, una distribución ampliamente utilizada para modelar índices. Esta opción se puede utilizar al estimar la intensidad o la probabilidad de que ocurra un evento. El modelo de distribución de probabilidad binomial supone lo siguiente:

• Los recuentos de eventos (numerador) son un subconjunto de la población (denominador).
• Cada evento es independiente de los demás eventos.
• La probabilidad de que ocurra un evento es la misma para todos los eventos.

Si alguno de estos supuestos no se cumple, la distribución binomial no es un modelo adecuado. Se recomienda seleccionar la distribución binomial solo cuando se cumplan estos supuestos y la probabilidad del evento no sea rara.

Bayes empírico local

La estimación del índice Bayes empírico local de una entidad es el promedio ponderado del índice bruto de la entidad focal y el índice promedio ponderado de su vecindad. El índice de Bayes empírico local se calcula de la siguiente manera:

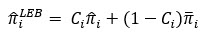
donde i es la entidad de interés, 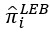es la estimación de índice Bayes empírico local, C_i es la ponderación, 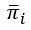es el índice promedio ponderado de la entidad i y sus vecinos, y la es el índice bruto de la entidad focal.

El índice promedio de una vecindad de entidades, 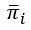, está determinada por los valores de los parámetros Tipo de vecindad y Esquema de ponderación local. El parámetro Tipo de vecindad especifica el método que se utilizará para identificar los vecinos de cada entidad. A cada vecino se le asigna una ponderación basada en el valor del parámetro Tipo de vecindad o Esquema de ponderación local. Luego, la herramienta calcula el índice promedio ponderado localmente de cada vecindad de la siguiente manera:

donde i es la entidad de interés, es el índice promedio ponderado localmente en i, j es el vecino, w_ij es la ponderación del vecino j, y 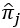es la estimación del índice bruto de vecino j.

Promedio ponderado localmente

El método de índice promedio ponderado localmente estima el índice de una entidad calculando el índice promedio ponderado de su vecindad. Para estimar los índices promedio ponderados localmente, la herramienta primero aplica el valor del parámetro Tipo de vecindad para identificar los vecinos de cada entidad. A continuación, a cada vecino se le asigna una ponderación basada en el valor del parámetro Tipo de vecindad o Esquema de ponderación local. El índice promedio ponderado localmente de cada entidad se calcula de la siguiente manera:

donde i es la entidad de interés, es el índice promedio ponderado localmente en i, j es el vecino, w_ij es la ponderación del vecino j, y 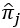es la estimación del índice bruto de vecino j.

Mediana ponderada localmente

El método de índice medio ponderado localmente estima el índice de una entidad calculando el índice medio ponderado de su vecindad.

Métodos locales

Los métodos locales utilizan los vecinos de una entidad para estimar su índice. Los vecinos se identifican utilizando el valor del parámetro Tipo de vecindad especificado y, a continuación, se asigna una ponderación a cada vecino.

Más información sobre los tipos de vecindades

Las ponderaciones de los vecinos pueden no estar ponderadas o calcularse mediante una función de ponderación geográfica (kernel). El parámetro Esquema de ponderación local admite las siguientes opciones de ponderación de vecinos: No ponderado, Gaussiano y Bicuadrado. Utilice el esquema de ponderación que mejor refleje la influencia que tienen los recuentos de eventos vecinos en los recuentos de eventos de una entidad focal. Si todos los vecinos influyen en la entidad focal, independientemente de la distancia, utilice la opción Sin ponderar.

Si la influencia de un vecino depende de la distancia, los vecinos más alejados de la entidad focal deberían tener menos peso y menos influencia en el índice estimado de la entidad focal. Los vecinos que están más cerca de la entidad focal deberían tener mayor peso y mayor influencia en el índice estimada. En este caso, utilice la opción Gaussiano o Bicuadrado. Estas opciones calculan las ponderaciones utilizando un kernel, que es una función que determina la rapidez con la que los pesos disminuyen a medida que aumentan las distancias. Tanto la función kernel gaussiana como la bicuadrada asignan una ponderación de uno a la entidad focal y disminuyen gradualmente la ponderación a medida que aumenta la distancia desde la entidad focal. Si se compara un esquema de ponderación bicuadrado con un esquema de ponderación Gaussiano con las mismas especificaciones de vecindad, los pesos disminuirán más rápidamente con el bicuadrado.

Si se especifican las opciones Gaussiano o Bicuadrado, también debe establecer el parámetro Ancho de banda del kernel. Defina un ancho de banda del núcleo adecuado en función de sus datos. Si no proporciona un valor, se estima un valor predeterminado.

Más información sobre cómo funciona Densidad kernel.

Multiplicador de índice

Cada índice es un valor entre 0 y 1. Si el tamaño de la población es grande o el evento de interés es raro, los índices resultantes serán pequeños. Los índices incluirán muchos ceros a la izquierda, lo que puede dificultar la interpretación de los índices. El parámetro Multiplicador de índice es un valor entero que escala los índices, por lo que son más significativos y más fáciles de interpretar. Si el multiplicador del índice es 100, se calcula un porcentaje. Una buena regla general es utilizar el valor de índice más pequeño para determinar el multiplicador de índice. Por ejemplo, si el índice más pequeño tiene tres ceros a la izquierda, el valor Multiplicador de índice debe ser 10.000 o más. El índice mínimo que no sea 0, será mayor que 1.

Cuando configura el valor de Multiplicador de índice, los índices se expresan como recuento previsto por unidades de multiplicador de índice. Por ejemplo, si calcula la tasa de mortalidad por cáncer de páncreas y configura el valor de Multiplicador de índice en 100.000, los índices resultantes serán el recuento previsto en 100.000 personas. Una entidad con un índice de 144 indicaría que se espera que se produzcan 144 muertes por cáncer de páncreas al año en cada grupo de 100.000 personas.

Salidas de la herramienta

La herramienta produce una clase de entidad o tabla de salida, una capa de grupo de salida y mensajes de geoprocesamiento.

Entidades o tabla de salida

La clase de entidades o tabla de salida incluye varios campos.

Índice excedente

El campo Excess Rate compara el índice de una entidad con el índice promedio de todas las entidades. El índice excedente se calcula dividiendo el índice observado de una entidad por el índice promedio de todas las entidades. El índice excedente puede ser cualquier valor positivo mayor o igual a cero. Los valores de índice excedente cercanos a uno indican que el índice estimado es similar al índice promedio. Si el índice excedente es menor que uno, el índice estimado de la entidad es menor que el índice promedio. Si el índice excedente es mayor que uno, el índice estimado de la entidad es mayor que el índice promedio. Por ejemplo, si una entidad tiene un índice excedente de 1,25, su índice es un 25 por ciento mayor que el índice promedio. Por el contrario, si una entidad tiene un índice excedente igual a 0,75, su índice es un 25 por ciento menor que el índice promedio.

Índice estandarizado

El campo Standardized Rate muestra cuánto se desvió el índice de una entidad del índice medio. El índice estandarizado se calcula de la siguiente manera:

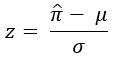
donde z es el índice estandarizado, es la estimación de índice, es el índice medio y 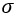es la desviación estándar. Las entidades con índices estandarizados negativos tienen índices menores que el índice medio. Las entidades con índices estandarizados positivos tienen índices mayores que el índice medio. Cuanto más negativo es el valor de un índice estandarizado, más se desvía por debajo del valor medio. Cuanto mayor es el valor de un índice estandarizado positivo, más se desvía por encima del valor medio. Las entidades con índices estandarizados mayores que 3 o menores que –3 se consideran valores atípicos.

Intervalos de confianza

Si el valor del parámetro Método de índice se establece en Índice bruto, la tabla o la clase de entidad de salida incluirá un campo Confidence Interval – Upper 95% y Confidence Interval- Lower 95%. El intervalo de confianza del 95 por ciento se calcula utilizando la metodología propuesta por el Centro para el Control de Enfermedades (CDC) del Centro Nacional de Estadísticas Sanitarias. Si el recuento de una entidad es mayor o igual a 100, una aproximación gaussiana es apropiada y, como resultado, el intervalo de confianza del 95 por ciento para el índice bruto se calcula de la siguiente manera:

Donde r_i es el índice bruto y Y_i es el recuento.

Si el número de recuentos es inferior a 100, el intervalo de confianza del 95 por ciento se calcula utilizando un método propuesto por K. Ulm en Un método sencillo para calcular el intervalo de confianza de un índice de mortalidad estandarizado (SMR). En este caso, la aproximación gaussiana de Poisson no es apropiada y se utiliza una identidad entre las probabilidades acumuladas de Poisson y la distribución chi cuadrado. Sea qgamma(p,x) el cuantil asociado con la probabilidad, p, de una distribución gamma con el parámetro de forma x y el parámetro de velocidad 1. Luego, el intervalo de confianza del 95 por ciento se calcula de la siguiente manera:

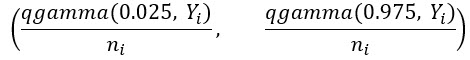
Fiable

Los valores del campo Reliable reflejan la fiabilidad de la estimación del índice. Este campo se incluye en la tabla o entidades de salida si el valor del parámetro Método de índice está establecido en Índice bruto. El cálculo sigue el método descrito por el CDC en su manual de referencia. Cuando el valor fiable es grande, la estimación del índice bruto es imprecisa y el índice bruto se considera poco fiable. A partir de 1989, el CDC en su Centro Nacional de Estadísticas Sanitarias consideraron que cualquier índice bruto que se basara en menos de 20 recuentos era estadísticamente poco fiable. Esto equivale a un valor fiable mayor o igual a 22,94.

La fiabilidad se mide a través del error estándar relativo (RSE), también conocido como coeficiente de variación. El RSE es la relación entre el error estándar del índice y la estimación del índice multiplicado por 100. La varianza del índice se calcula de la siguiente manera:

y suponiendo un recuento distinto de cero, el RSE se calcula de la siguiente manera:

RSE solo depende de los recuentos (Y_i). Aunque la fórmula RSE no depende directamente del tamaño de la población, las poblaciones grandes tienden a tener un mayor número de recuentos, por lo que existe un efecto indirecto.

Número de vecinos no nulos

El campo Number of Non-Null Neighbors enumera la cantidad de vecinos, incluida la entidad focal, que no tienen un índice nulo. Las entidades con un valor negativo o nulo en los valores del parámetro Campo de población o Campo de recuento tienen un índice nulo.Los métodos de suavizado espacial utilizan la vecindad de una entidad para determinar el índice de esa entidad. El campo Number of Non-Null Neighbors revela la cantidad de vecinos que se utilizaron para suavizar el índice de la entidad focal. Este campo se incluye en la tabla o clase de entidad de salida si el valor del parámetro Método de índice es Promedio ponderado localmente, Mediana ponderada localmente o Bayes empírico local.

Rellenar valor faltante

El campo Fill Missing Value es un campo booleano que indica si se imputó un índice para la entidad. Las entidades con un valor negativo o nulo en el valor del parámetro Campo de recuento o un valor negativo o nulo en el valor del parámetro Campo de población tendrán un índice nulo. Sin embargo, si el valor del Método de índice es Promedio ponderado localmente o Mediana ponderada localmente, se puede imputar un índice para una entidad con un índice nulo. Si la entidad tiene vecinos no nulos, el índice nulo será reemplazada por el promedio ponderado localmente o la estimación mediana ponderada localmente de su vecindad.

Capa de grupo y simbología

La herramienta agrega una capa de grupo al panel Contenido y una subcapa para cada índice. Si se calculan más de 10 índices, solo los primeros 10 índices se agregarán como subcapas.

Cada subcapa es un mapa de desviación estándar. Los índices se dividen en bins según su desviación estándar. Cada bin está etiquetado con el intervalo de desviación estándar y, entre paréntesis, el intervalo de índice correspondiente. La rampa de colores incluye tres colores: verde, blanco en el medio y marrón. La rampa de color se centra en torno al índice medio. Las entidades sombreadas en verde tienen índices que están por debajo del índice medio. Las entidades sombreadas en marrón tienen índices superiores al índice medio. Las entidades con tonos más fuertes de color marrón (+3 desviaciones estándar) y verde (-3 desviaciones estándar) son valores atípicos.

Mensajes de geoprocesamiento

Los mensajes de geoprocesamiento proporcionan un resumen de las entidades y los índices. Los mensajes incluyen una sección desplegable para cada índice calculado. Cada sección incluye una tabla de Resumen de índices. Si el valor del parámetro Método de índice es Promedio ponderado localmente, Mediana ponderada localmente o Bayes empírico local, cada sección también incluirá una tabla de Resumen de recuentos de vecindades.

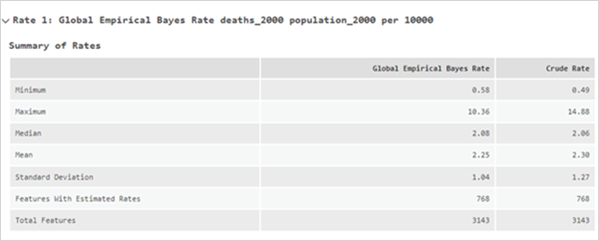
Resumen de índices

Si el valor del parámetro Método de índice no es Índice bruto, la tabla Resumen de índices incluirá una columna que resume el método de índice seleccionado y una columna adicional que resume los índices brutos. Utilice estas columnas para comparar los resultados del método de índice seleccionado con los resultados del método de índice bruto. La tabla Resumen de índices incluye los valores de Mínimo, Máximo, Mediana, Valor medio y Desviación estándar de los índices. Si el valor del parámetro Método de índice es Promedio ponderado localmente o Mediana ponderada localmente, la tabla incluirá una fila Entidades con valor de índice nulo y Entidades con valores completos. La fila Entidades con valor de índice nulo enumera la cantidad de entidades con un índice nulo. La fila Entidades con valores completos enumera la cantidad de entidades con un índice imputado. Estas entidades inicialmente tenían un índice nulo; sin embargo, su vecindad incluía valores de índice no nulos, por lo que se imputó su índice.

Resumen de recuentos de vecindades

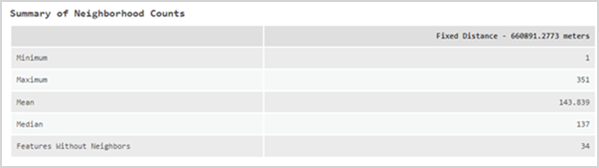
Si el valor del parámetro Método de índice es Promedio ponderado localmente, Mediana ponderada localmente o Bayes empírico local, cada sección también incluirá una tabla de Resumen de recuentos de vecindades, que resume todas las vecindades. La tabla incluye el recuento de vecindad Mínimo, Máximo, Mediano y Medio y el número del valor Entidades sin vecinos.

Recursos adicionales

Consulte los siguientes recursos adicionales:

• Anselin, L., N. Lozano y J. Koschinsky. 2006."Rate Transformations and Smoothing"
• Brillinger, D. R. 1986. "A biometrics invited paper with discussion: the natural variability of vital rates and associated statistics." Biometrics, 693-734. https://pubmed.ncbi.nlm.nih.gov/3814721/
• Carlin, B.P. y T.A. Louis. 1997. "Bayes and empirical Bayes methods for data analysis." Statistics and Computing, 153- 154. https://doi.org/10.1023/A:1018577817064
• Marshall, R.J. 1991. "Mapping disease and mortality rates using empirical Bayes estimators." Journal of the Royal Society Series C: (Applied Statistics), 283-294. https://doi.org/10.2307/2347593
• Martuzzi, M. y P. Elliott. 1996. "Empirical Bayes estimation of small prevalence of non-rare conditions." Statistics in Medicine, 15(17-18) 1867-1873. https://doi.org/10.1002/(SICI)1097-0258(19960915)15:17<1867::AID-SIM398>3.0.CO;2-2
• National Center for Health Statistics. 2019. Technical appendix from vital statistics of United States 1999 mortality
• Ulm, K. 1990. "Simple method to calculate the confidence interval of a standardized mortality ratio (SMR)." American Journal of Epidemiology, 131(2) 373-375. https://doi.org/10.1093/oxfordjournals.aje.a11507