La herramienta Evaluar los tamaños de los bins para la agregación de puntos ayuda a elegir un tamaño de bin adecuado al agregar cantidades de puntos en bins cuadrados o hexagonales dispuestos en una teselación. La herramienta permite evaluar otros tamaños de bin para determinar cómo podrían cambiar los recuentos y patrones resultantes si se utilizan otros tamaños de bin en su lugar.

Agregar y contabilizar puntos contenidos en bins es un flujo de trabajo común en SIG, lo que incluye agregar llamadas de emergencia, interrupciones del servicio y avistamientos de animales. También se utiliza para visualizar mejor grandes aglomeraciones de puntos y proteger la confidencialidad ocultando ubicaciones de puntos individuales. Sin embargo, a pesar de las muchas aplicaciones, existe relativamente poca orientación sobre el tamaño que deberían tener estos bins. En la práctica, los tamaños de bin suelen elegirse por conveniencia (por ejemplo, utilizando un número redondo) o seleccionando el tamaño de bin que produce resultados más atractivos visualmente. Sin embargo, la elección de la escala cambia lo que puede detectar y cómo interpretarlo (ejemplo de problema de unidad aérea modificable), por lo que es importante tomar decisiones defendibles y reproducibles. También es importante caracterizar cuán sensibles son las cantidades de puntos resultantes al tamaño del bin: ¿usar un bin más grande o más pequeño daría lugar a patrones y conclusiones diferentes?
En esencia, determinar un tamaño de bin apropiado para agregar datos de puntos en bins es un problema de escala. Los bins que son demasiado pequeños estarán vacíos en su mayoría y tendrán recuentos poco fiables y los bins que son demasiado grandes se difuminarán y enmascararán patrones locales importantes. El tamaño de bin adecuado es lo bastante grande para producir una gran variedad de cantidad de puntos (en lugar de tener muchos bins vacíos con un pequeño número de cantidades grandes), pero lo bastante pequeño como para que los patrones de puntos locales se conservan en los bins resultantes (en lugar de agregarse y perderse).
Para determinar un tamaño de bin adecuado, se avalúa un rango de tamaños de bins candidatos en función de dos criterios: uniformidad interna y variedad de cantidad de puntos. La métrica de uniformidad interna mide si los puntos de cada bin tienden a ser espacialmente aleatorios y casi siempre se prefieren los tamaños de bin más pequeños. Por el contrario, la métrica de variedad de cantidad de puntos mide cuán uniformemente distribuidos están los bins resultantes y casi siempre se prefieren los tamaños de bin más grandes.

Estas dos métricas (cada valor entre 0 y 1) se multiplican a la vez para producir una sola puntuación de evaluación para cada tamaño de bin y la herramienta recomienda el tamaño de bin con la puntuación de evaluación más alta. La curva de puntuación de evaluación también permite ver cómo se comparan otros tamaños de bin con el tamaño de bin recomendado por la herramienta.

Consulte la sección Detalles adicionales de evaluación de tamaño de bins a continuación para obtener más información sobre las puntuaciones de evaluación y cómo se calculan.
Definir un límite de agregación adecuado
Además de proporcionar los puntos que se agregarán, también debe utilizar el parámetro Límite de agregación para definir el área en la que se agregarán los puntos y se crearán los bins. El límite de agregación (a veces denominado área de estudio o área de interés) debería definir el área en la que pueden producirse y registrarse puntos. Por ejemplo, al agregar llamadas de emergencia dentro de una ciudad, la frontera de la ciudad debería utilizarse como límite de agregación porque la llamada de emergencia puede proceder de cualquier parte de la ciudad y las llamadas que no se realicen dentro de la ciudad no se incluirán en el dataset. Aunque resulta tentador considerar que los bins se crean y recortan según el límite de agregación, en realidad el límite tiene un impacto profundo en las puntuaciones de evaluación y en el tamaño de bin recomendado. La elección de un límite de agregación inadecuado suele ocasionar tamaños de bin recomendados grandes o pequeños de manera poco realista, por lo que es muy recomendable tener en cuenta el límite que es más adecuado para los datos.
Es importante proporcionar un límite para delinear dónde pueden ocurrir los puntos y dónde no porque la herramienta debe ser capaz de diferenciar si una zona no tiene puntos porque no se han producido incidencias (como una zona de una ciudad en la que no se han producido robos en una semana concreta) o si no es posible observar puntos en la zona (como avistamientos de ballenas en tierra). Como esta herramienta evalúa la variedad de cantidades de puntos resultantes de los bins, las cantidades cero son igual de importantes que otras; la herramienta evitará los tamaños de bin que resulten en una proporción de bins sin puntos. En la práctica, esto significa que, si el límite de agregación es demasiado grande (lo que implica que contiene muchas áreas en las que no pueden registrarse puntos), el tamaño de bin recomendado será irrealmente grande con el fin de rellenar los vacíos y reducir el número de bins vacíos. Por el contrario, si el área de estudio es demasiado pequeña, la herramienta recomendará tamaños de bin más pequeños para aumentar el número de bins sin puntos.
Si se conoce un límite de agregación apropiado para los puntos (como el límite de una ciudad), seleccione la opción Polígonos personalizados y proporcione el límite en el parámetro Polígonos personalizados. También puede dibujar interactivamente el límite de agregación mediante el uso de la entrada interactiva de entidades.
Si no se conoce el límite de agregación adecuado, el límite puede crearse automáticamente con las opciones Envoltura cóncava, Envoltura convexa o Envoltura (consulte Geometría de límite mínima para obtener más información). Cuando utilice un límite creado de forma automática, siempre debería evaluar visualmente si el límite representa los puntos de manera adecuada. Si el límite no es adecuado, utilice una opción diferente o dibuje un límite que represente los puntos de forma interactiva.
En la imagen siguiente se muestran los tamaños de bin resultantes correspondientes a los mismos datos que utilizan todas las opciones del parámetro Límite de agregación. La opción personalizada utiliza el límite real en el que se recopilan los puntos. Para otros datasets (sobre todo, los que tienen valores espaciales atípicos), la diferencia en cuanto a tamaños de bin resultantes y patrones puede ser todavía más exagerada.

Salidas de la herramienta
La herramienta crea tres salidas que se incluyen en una capa de grupo. La salida principal es una clase de entidad de polígono de los bins agregados que utilizan el tamaño de bin recomendado. La capa está simbolizada por la cantidad de puntos que hay dentro de cada bin.
La segunda salida es una clase de entidad de polígono del límite de agregación que ha utilizado la herramienta. Esta salida es más útil para las opciones de envoltura cóncava y convexa a fin de visualizar las formas de los límites. La tercera salida es una tabla que contiene las puntuaciones de evaluación correspondientes a todos los tamaños de bin que ha probado la herramienta. La tabla se suministra con dos gráficos que pueden utilizarse para investigar los tamaños de bin.
Gráfico de puntuaciones de evaluación en función del tamaño de los bins
El gráfico de puntuaciones de evaluación en función del tamaño de los bins muestra las puntuaciones de evaluación de todos los tamaños de bin sometidos a prueba. Los puntos azules del gráfico son las puntuaciones de evaluación sin procesar de los tamaños de bin y se suavizan con una spline (la curva azul). El valor más grande de la curva azul es el tamaño de bin recomendado y se indica mediante una línea naranja vertical. También se muestra una región de confianza en color naranja claro alrededor del tamaño de bin recomendado, y cualquier tamaño de bin dentro de este rango tiene una puntuación de evaluación que no es significativamente menor que el tamaño de bin recomendado, por lo que puede elegir cualquier valor en este rango (por ejemplo, un número redondo) sin una disminución significativa en la puntuación de evaluación.

El tamaño de bin recomendado y el área asociada de cada bin se muestran en la parte inferior del gráfico. En el caso de los bins cuadrados, el tamaño de bin es la anchura o la altura de cada cuadrado; en el caso de los hexágonos, el tamaño de bin es la altura de cada hexágono (las distancia desde un borde plano hasta el contrario).
Nota:
El tamaño de bin más pequeño probado (el valor mínimo del eje x) es el tamaño de bin que da como resultado 20 bins por cada punto de entrada (en otras palabras, los bins son tan pequeños que más del 95% de ellos no contendrán puntos) y el tamaño de bin más grande (el valor máximo del eje x) corresponde al 25% de la extensión en x o en y, la que sea mayor. La herramienta prueba 100 tamaños de bin incrementados de manera uniforme entre el mínimo y el máximo.
Gráfico de uniformidad interna y variedad de la cantidad de puntos en los distintos tamaños de bin
El gráfico Uniformidad interna y variedad de cantidad de puntos en los tamaños de bin muestra los dos criterios que se combinaron para generar las puntuaciones de evaluación. Por cada tamaño de bin testado, una curva verde muestra la puntuación de uniformidad interna y la curva morada muestra la puntuación de variedad de cantidades de puntos. Por lo general, la curva verde se reducirá y la curva morada aumentará. También se muestran el tamaño de bin recomendado y el intervalo de confianza como referencia. El tamaño de bin recomendado generalmente tendrá puntuaciones razonables en ambos criterios, lo que indica un equilibrio eficaz entre los criterios opuestos. Consulte la sección Detalles adicionales de evaluación de tamaño de bins a continuación para obtener más información sobre cada criterio.

Mensajes de geoprocesamiento
Los mensajes de la herramienta incluyen una sección Resumen de resultados y una sección Resumen de agregación. El resumen de resultados muestra el tamaño de bin recomendado y el área de bin asociada. En el caso de los hexágonos, muestra la longitud del lado de cada hexágono. El resumen de agregación contiene varias estadísticas de resumen de las cantidades de puntos y los bins resultantes, como el número de puntos, el número de bins, el recuento medio de puntos y el área del límite de agregación.
Prácticas recomendadas y limitaciones
A continuación, se mencionan las prácticas recomendadas y las limitaciones al utilizar esta herramienta:
La herramienta asume que existe un único tamaño de bin apropiado para agregar los puntos. Sin embargo, en muchos casos no existe un único tamaño de bin que represente adecuadamente los puntos en todo el límite de agregación. Por ejemplo, en un condado grande que tiene áreas rurales con baja densidad de población y áreas urbanas con alta densidad de población, puede resultar difícil agregar llamadas de emergencia en todo el condado. Los bins que son lo bastante pequeños como para representar las áreas urbanas de forma adecuada estarán prácticamente vacíos en áreas rurales, mientras que los bins lo bastante grandes para áreas rurales concentrarán los centros urbanos en unos cuantos bins. Un signo común de este problema son los intervalos de confianza muy amplios alrededor del tamaño de bin recomendado, lo que indica una gran incertidumbre sobre qué tamaño de bin utilizar. Una posible solución es separar los puntos en datasets diferentes y agregarlos por separado utilizando tamaños de bin diferentes.
- La herramienta es más adecuada cuando pretende realizar algún tipo de análisis usando cantidades de puntos resultantes (por ejemplo, análisis de puntos calientes o análisis de valores atípicos locales) en lugar de suavizado cartográfico simple. Aunque puede ser eficaz suavizar grandes aglomeraciones de puntos para una mejor representación visual, el propósito principal de la herramienta es generar bins agregados que conserven de la mejor manera la estructura espacial de los puntos y produzcan cantidades de puntos adecuadas para el análisis.
- Los números elevados de puntos de coincidencia (varios puntos en la misma coordenada) pueden producir tamaños de bin no realistas. La herramienta devolverá una advertencia si cualquiera de los puntos de entrada coinciden.
Detalles adicionales de la evaluación de tamaño de bins
La metodología general de la herramienta es evaluar un rango de tamaños de bin utilizando dos métricas: uniformidad interna y variedad de cantidad de puntos. A cada tamaño de bin se asigna una puntuación entre 0 y 1 para cada métrica y los valores se multiplican a la vez para generar una puntuación de evaluación final que equilibra ambos criterios. La métrica de uniformidad interna generalmente prefiere tamaños de bin más pequeños, mientras que la métrica de variedad de cantidad de puntos suele preferir tamaños de bin más grandes. Por lo tanto, los tamaños de bin con las puntuaciones de evaluación más altas son los intermedios que logran el mejor compromiso entre los criterios opuestos. En las secciones siguientes se describen los dos criterios.
Uniformidad interna
La métrica de uniformidad interna mide si los puntos están distribuidos de manera uniforme dentro de los bins resultantes. Por ejemplo, en la imagen siguiente, los puntos del bin de la izquierda están muy agrupados en una esquina, pero los puntos están distribuidos de forma aleatoria y uniforme por el bin de la derecha, por lo que el bin de la derecha tiene la uniformidad interna más alta.
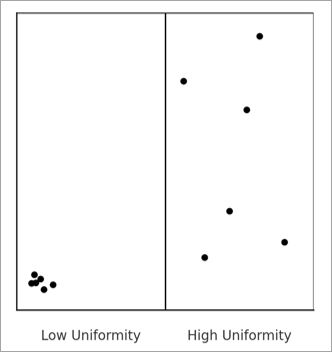
La uniformidad interna es importante para evitar la elección de un tamaño de bin que oculte patrones locales importantes. Si los puntos de un bin forman un clúster o patrón potente, resumirlos en un solo recuento puede ser engañoso. Esta métrica comprueba si los puntos de cada bin están organizados de forma aleatoria, lo que sugiere que el bin es un resumen imparcial y representativo de los puntos que contiene. Cuando muchos bins presentan patrones estructurados, es un signo de que el tamaño de bin podría ser demasiado grande, ocultando patrones importantes dentro de los bins.
La métrica se calcula probando la aleatoriedad espacial completa de cada bin; el valor es la proporción de bins con valor p mayor que 0,05 (lo que significa que no se detectó que estuvieran agrupados). Los bins sin puntos no se incluyen en la proporción porque las celdas vacías no se pueden clasificar como agrupadas o aleatorias espacialmente.
La prueba de aleatoriedad espacial completa divide cada bin en una serie de bins más pequeños. En el caso de los cuadrados, el bin se divide en 25 cuadrados más pequeños; en lo que respecta a los hexágonos, el bin se divide en 24 triángulos. Luego se prueba la uniformidad de los recuentos de puntos dentro de cuadros o triángulos mediante una prueba de bondad de ajuste de chi cuadrado.
Variedad de cantidad de puntos
La métrica de variedad de cantidad de puntos cuantifica la diversidad de las cantidades de puntos entre los bins y favorece los tamaños de bin que producen una amplia variedad de valores de cantidad, evitando aquellos tamaños de bin que presentan grandes proporciones de bins vacíos junto con un pequeño número de bins con cantidades elevadas. Conceptualmente, esto fomenta la riqueza informativa, lo que refleja la idea de que las agregaciones deben producir una variación y diversidad significativas en las cantidades de puntos, lo cual es especialmente deseable cuando se pretende realizar un análisis (como un análisis de puntos calientes) sobre las cantidades de puntos. En la práctica, esta métrica tiende a aumentar el tamaño de bin, ya que los bins más grandes tienden a acumular cantidades más diversas y distribuidas de manera uniforme.
Por ejemplo, en la imagen siguiente, los bins de la parte inferior producen una variedad mayor y una distribución más uniforme de las cantidades de puntos que los bins de la parte superior, por lo que los bins de la parte inferior recibirán una puntuación más alta en cuanto a variedad de cantidad de puntos. En general, cuanto más uniforme (plana) es la distribución de las cantidades de puntos, más alta es la puntuación.

La métrica se calcula utilizando una medida de entropía de Shannon normalizada. La distribución de las cantidades de bins se divide en cinco intervalos iguales para cada tamaño de bin, y se calcula la entropía de esta distribución. Esta entropía se divide después entre la entropía de una distribución uniforme, lo que produce una puntuación entre 0 y 1.
Nota:
Las puntuaciones de uniformidad interna y de variedad de cantidad de puntos se generan simulando cuadrados o hexágonos aleatorios dentro del límite de agregación, en lugar de construir una teselación completa para cada tamaño de bin. Esto mejora la velocidad de procesamiento, pero los resultados serán un poco diferentes cuando se vuelva a ejecutar la herramienta. Sin embargo, puede utilizar el entorno Generador de números aleatorios para garantizar resultados reproducibles. El número de polígonos simulados para cada tamaño de bin se calcula de modo que, en promedio, el 75% del límite de agregación quede cubierto por las simulaciones.
Intervalos de confianza con bootstrap
Los intervalos de confianza naranjas en torno al tamaño de bin recomendado en los gráficos se construyen utilizando bootstrapping. Este proceso vuelve a muestrear aleatoriamente las puntuaciones de evaluación con reemplazo y estima una spline para cada conjunto remuestreado de puntuaciones de evaluación. Para cada remuestreo, se registra la puntuación de evaluación del tamaño de bin recomendado original y se determina el quinto percentil. Todo tamaño de bin cuya puntuación de evaluación supere este valor se incluirá en el intervalo de confianza. Estos tamaños de bin pueden interpretarse como que tienen puntuaciones de evaluación que no son significativamente menores que la puntuación de evaluación del tamaño de bin recomendado por la herramienta.
Hexágonos H3
La herramienta no permite la agregación en hexágonos H3. Sin embargo, al agregar en hexágonos H3, puede mostrar las resoluciones H3 asociadas como guías en el gráfico de puntuaciones de evaluación en función del tamaño de los bins. Las guías están deshabilitadas de forma predeterminada, pero es posible habilitarlas en la pestaña Guías del panel Propiedades de gráfico.

Cuando se habilitan, las guías (líneas verticales discontinuas grises) permiten ver las puntuaciones de evaluación de las resoluciones H3 que están dentro del rango de tamaños de bin sometidos a prueba y elegir el mejor para sus datos. Por ejemplo, en la imagen siguiente, la resolución H3 4 tiene la puntuación de evaluación más alta, está más próxima al tamaño de bin recomendado y está dentro del intervalo de confianza.

Referencias
Para implementar la herramienta, se utilizaron los siguientes recursos:
- Ramos, Rafael G. 2025. "Finding an Adequate Areal Unit to Map Crime: A Spatial Data Perspective." New Research in Crime Modeling and Mapping Using Geospatial Technologies (pp. 27-44). Cham: Springer Nature Switzerland. https://doi.org/10.1007/978-3-031-81580-5_2.