Muchas herramientas y métodos de la caja de herramientas Estadísticas espaciales requieren definir relaciones espaciales entre entidades. Esto conlleva identificar las entidades que se consideran próximas entre sí y cuánta influencia deben tener unos vecinos en otros. Esta estructura, definida por medio de la combinación de un tipo de vecindario y un esquema de ponderación, constituye los cimientos de muchos análisis espaciales.
Relaciones espaciales
Una diferencia importante entre las estadísticas espaciales y tradicionales es que las estadísticas espaciales integran relaciones espaciales directamente en sus operaciones matemáticas y modelos. Por consiguiente, varias herramientas tienen un parámetro Conceptualización de relaciones espaciales, Tipo de vecindario o Restricción espacial que permite definir las relaciones espaciales entre entidades.
Las relaciones espaciales diferentes destacan aspectos diferentes de la estructura espacial. Por ejemplo, en un estudio del mercado de la vivienda, podría tener sentido definir el vecindario de cada casa como las pocas propiedades más cercanas, ponderadas por distancia, bajo el supuesto de que las ventas cercanas ejercen la mayor influencia. Otras situaciones pueden requerir definiciones más amplias o complejas, como relacionar las ciudades en función del número de viajeros entre ellas (donde las ciudades que están más alejadas geográficamente podrían seguir teniendo una elevada dependencia económica). Estas opciones afectan a todo, desde la detección de patrones espaciales hasta el comportamiento de los modelos espaciales, por lo que es importante reflexionar sobre qué relaciones espaciales son más adecuadas para los datos y las preguntas.
Al llevar a cabo un análisis estadístico espacial, como un análisis de puntos calientes o un análisis de clúster y valor atípico, puede definir las relaciones espaciales directamente en las herramientas mediante el uso de los parámetros de las herramientas. Sin embargo, también puede crear un archivo de matriz de ponderaciones espaciales (.swm) para almacenar los vecinos y las ponderaciones de manera que puedan utilizarse otra vez en varias herramientas.
Las herramientas y los métodos diferentes ofrecen varias opciones para definir las relaciones espaciales. Si bien ninguna herramienta admite todas las relaciones posibles, la herramienta Generar matriz de ponderaciones espaciales permite la mayor variedad de relaciones espaciales, y el archivo de salida puede usarse y reutilizarse en otras herramientas de análisis. Para todas las relaciones espaciales excepto las más simples, se recomienda definir primero las relaciones espaciales en un archivo de matriz de ponderaciones espaciales y luego usar ese archivo en las herramientas de análisis espacial.
En las secciones siguientes se describen las diferentes relaciones espaciales que admiten las herramientas:
Distancia inversa
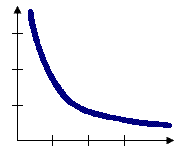
La relación espacial de distancia inversa es un tipo de impedancia, o disminución de la distancia, en la que el peso de las entidades vecinas disminuye al dividirse por la distancia entre la entidad vecina y la entidad focal. Todas las entidades afectan o influyen en el resto de entidades, pero cuanto más lejos esté algo, menor impacto tendrá. Esta distancia inversa también se eleva habitualmente a una potencia, como la distancia inversa al cuadrado, lo que provoca que el peso disminuya aún más rápido. Normalmente, se recomienda utilizar una distancia de umbral con las relaciones de distancia inversa para reducir el número de vecinos con ponderaciones muy próximas a 0. Cuando se especifica la distancia de umbral, se calcula un valor de umbral predeterminado, pero puede imponer que todas las entidades sean un vecino de todas las demás mediante la configuración de la distancia de umbral en 0.
Banda de distancia fija

La relación espacial de banda de distancia fija impone una esfera de influencia alrededor de cada entidad e incluye como vecinas todas las entidades que se encuentren dentro de una distancia de umbral determinada alrededor de la entidad focal. Esta opción es adecuada cuando se quiere evaluar las propiedades estadísticas de los datos en una escala espacial (fija) particular. Si estudia los patrones de viajes y sabe que el viaje promedio para trabajar es de 15 millas, por ejemplo, es posible que desee utilizar una distancia fija de 15 millas para su análisis. Consulte Mejores prácticas para seleccionar un valor de banda distancia fija para conocer las estrategias que pueden ayudarle a identificar una escala apropiada de análisis.
Zona de indiferencia
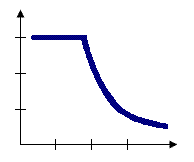
La relación espacial de zona de indiferencia combina las relaciones espaciales de banda de distancia fija y de distancia inversa. Las entidades dentro de la distancia de umbral se incluyen en los análisis para la entidad de destino. Una vez que se excede la distancia de umbral, el nivel de influencia (la ponderación) cae rápidamente. Este método resulta adecuado cuando desea mantener la escala de análisis fija, pero no desea imponer límites nítidos en las entidades vecinas incluidas en los cálculos de la entidad de destino.
Contigüidad de polígonos
Para las clases de entidad de polígono, puede optar por definir como vecinos todos los polígonos que sean contiguos al polígono focal. También puede elegir si incluir polígonos como vecinos si solo comparten una esquina (contigüidad tipo reina) o incluir únicamente como vecinos a los que comparten un borde (denominado contigüidad tipo torre). En varias herramientas, estas opciones se denominan Bordes y esquinas de contigüidad y Solo bordes de contigüidad, respectivamente. Si cualquier porción de dos polígonos se superpone, se considerarán vecinos según ambas opciones de contigüidad.

La contigüidad de polígono también puede ampliarse a órdenes superiores, en los cuales el orden corresponde al número de pasos necesarios para pasar del polígono focal a sus vecinos. La contigüidad de primer orden significa que solo los vecinos inmediatos del polígono focal serán vecinos (los que pueden alcanzarse en un solo paso). El orden dos significa que se incluirán como vecinos todos los polígonos a los que se pueda llegar en dos pasos o menos (los vecinos de primer orden y todos los vecinos de primer orden de estos). Si los polígonos se organizan en una cuadrícula, los órdenes superiores formarán anillos concéntricos alrededor del polígono focal. En general, se recomienda evitar el uso de polígonos de orden superior a 3. Puede crear relaciones espaciales de contigüidad de orden superior mediante el uso de la herramienta Generar matriz de ponderaciones espaciales.
K vecinos más próximos
La relación espacial de los k vecinos más cercanos utiliza como vecinos un número determinado de sus k entidades más próximas, donde k se indica en el parámetro Número de vecinos. En las ubicaciones donde la densidad de la entidad es alta, la escala espacial del análisis será más pequeña. Del mismo modo, en las ubicaciones donde la densidad de la entidad es escasa, la escala espacial para el análisis será más grande. Una ventaja para este modelo de relaciones espaciales es que asegura que habrá algunos vecinos para cada entidad de destino, aún cuando las densidades de la entidad varían ampliamente en el área de estudio.

Triangulación de Delaunay
La relación espacial Triangulación de Delaunay construye vecinos al crear triángulos de Voronoi a partir de entidades de puntos o centroides de la entidad, ya que cada punto o centroide es un nodo de triángulo. Los nodos conectados mediante un borde de triángulo se consideran vecinos. Utilizar la triangulación de Delaunay garantiza que cada entidad tendrá al menos un vecino, aún cuando los datos incluyan islas o densidades de entidades que varíen ampliamente. No utilice la opción Triangulación de Delaunay cuando tiene entidades coincidentes.

Ventana de tiempo-espacio
Con esta opción usted define las relaciones de entidades en términos de espacio (distancia fija) y una ventana de tiempo (intervalo de tiempo fijo). Esta opción está disponible cuando crea un archivo de matriz de ponderaciones espaciales mediante la herramienta Generar matriz de ponderaciones espaciales. Cuando selecciona la opción Ventana de espacio-tiempo, también es necesario que especifique valores en los parámetros Campo de fecha/hora, Tipo de intervalo fecha/hora (Horas, Días o Meses, por ejemplo) y Valor de intervalo fecha/hora. El valor del intervalo es un entero. Si seleccionó la opción Horas para el tipo de intervalo y 3 para el valor de intervalo, por ejemplo, dos entidades se considerarían vecinas si los valores en el campo de fecha/hora están a tres horas unos de otros. Con esta conceptualización, las entidades son vecinas si están dentro de la distancia especificada y del intervalo de tiempo especificado de la entidad de destino. Como posible ejemplo, seleccione la opción Ventana de espacio-tiempo del parámetro Conceptualización de relaciones espaciales si desea crear un archivo de matriz de ponderaciones espaciales para utilizarlo con Análisis de puntos calientes para identificar puntos calientes de espacio-tiempo. La información adicional, incluyendo la forma de visualizar los resultados, se presenta en Análisis de espacio-tiempo. Dispone de otras opciones para visualizar, en 3D, un cubo de espacio-tiempo de netCDF.
Obtener ponderaciones espaciales a partir del archivo
Si sus relaciones espaciales están definidas en un archivo de matriz de ponderaciones espaciales (.swm), use esta opción para proporcionar el archivo y aplicar las ponderaciones personalizadas al análisis. Puede crear estos archivos con la herramienta Generar matriz de ponderaciones espaciales, la herramienta Generar ponderaciones espaciales de red, el Explorador de vecindad o varias herramientas del conjunto de utilidades de componentes espaciales (vectores propios de Moran).
Prácticas recomendadas para seleccionar las relaciones espaciales
Cuanto más pueda modelar de manera realista cómo interactúan mutuamente las entidades en el espacio, más precisos serán sus resultados. Su elección en cuanto a relación espacial deberá reflejar relaciones inherentes entre las entidades que está analizando. A veces, la elección también estará influenciada por características de los datos.
Los métodos de distancia inversa, por ejemplo, son más adecuados con datos continuos o para modelar procesos en los que cuanto más cerca estén dos entidades en el espacio, más probable será que interactúen entre sí o que se influyan mutuamente. Con esta relación espacial, cada entidad es potencialmente vecina de la otra entidad, y con grandes datasets, el número de cálculos involucrados será enorme. Procure incluir una distancia de umbral siempre al utilizar las relaciones de distancia inversa. Esto es particularmente importante para datasets grandes. Si no proporciona una distancia de umbral, se calculará una, pero probablemente no sea la distancia más adecuada para su análisis. El umbral de distancia predeterminado será la distancia mínima que garantice que cada entidad tenga al menos un vecino.
La opción Banda de distancia fija funciona bien para datos de puntos y a menudo es una opción razonable para los datos de polígono cuando hay una gran variación en el tamaño del polígono (polígonos muy grandes en el borde del área de estudio y polígonos muy pequeños en el centro del área de estudio, por ejemplo), y desea garantizar una escala de análisis consistente. Consulte Mejores prácticas para seleccionar un valor de distancia fija a continuación para conocer las estrategias que lo ayudan a determinar un valor de banda de distancia apropiada para su análisis.
La opción Zona de indiferencia funciona bien cuando la distancia fija es adecuada, pero imponer límites nítidos en las relaciones de vecindad no es una representación precisa de sus datos. La relación de zona de indiferencia considera que cada entidad es vecina de las demás entidades.
Las relaciones de contigüidad de polígono (opciones Solo bordes de contigüidad y Bordes y esquinas de contigüidad) son efectivas cuando los polígonos son similares en tamaño y distribución, y cuando las relaciones espaciales son una función de la proximidad de los polígonos (la idea de que si dos polígonos comparten un límite, la interacción espacial entre ellos aumenta). Cuando selecciona una conceptualización de contigüidad de polígono, casi siempre deseará seleccionar estandarización de filas para las herramientas que tienen el parámetro Estandarización de filas.
La opción Vecinos K más cercanos es efectiva cuando desea asegurarse de que tiene un número mínimo de vecinos para su análisis. Especialmente cuando los valores asociados con sus entidades están sesgados (no están distribuidos normalmente), es importante que cada entidad se evalúe dentro del contexto de al menos ocho vecinos (esta es solamente una regla general). Cuando la distribución de los datos varía en el área de estudio de manera que algunas entidades están lejos de las demás entidades, este método funciona bien. Sin embargo, tenga en cuenta que el contexto espacial del análisis cambia según las variaciones en la escasez o densidad de sus entidades. Cuando fijar la escala de análisis es menos importante que fijar la cantidad de vecinos, el método K vecinos más próximos es apropiado.
La opción Triangulación de Dalaunay (a veces denominada vecinos naturales) es adecuada cuando los datos incluyen polígonos de isla (polígonos aislados que no comparten ningún límite con otros polígonos) o en casos donde hay una distribución espacial de entidades muy desigual.
La opción Ventana de espacio-tiempo le permite definir las relaciones de entidades en términos tanto de su proximidad espacial como de su proximidad temporal. Esta opción es adecuada, por ejemplo, para identificar puntos calientes de espacio-tiempo o construir grupos en los que la pertenencia está limitada por la proximidad de espacio y de tiempo. En el Análisis de espacio-tiempo se proporcionan ejemplos de análisis de espacio-tiempo así como estrategias para representar de un modo eficaz los resultados de este tipo de análisis.
Para algunas aplicaciones, la interacción espacial se modela mejor en términos del tiempo de viaje o de la distancia de viaje. Si modela la accesibilidad a los servicios urbanos, por ejemplo, o busca los puntos calientes de delitos urbanos, se recomienda modelar las relaciones espaciales en términos de una red. Utilice la herramienta Generar ponderaciones espaciales de red.
Si ninguna de las opciones predefinidas funciona bien en el análisis, puede crear un archivo de texto ASCII o una tabla con las relaciones de entidad a entidad que desee y utilizarlas para crear un archivo de matriz de ponderaciones espaciales. Si una de las opciones anteriores se aproxima a la relación espacial que desea, puede usar la herramienta Generar matriz de ponderaciones espaciales para crear un archivo básico de matriz de ponderaciones espaciales y, a continuación, editar su archivo de matriz de ponderaciones espaciales.
Esquemas de ponderación
Mientras que las relaciones espaciales de distancia inversa y de zona de indiferencia aplican directamente ponderaciones a todos los vecinos en función de la distancia, varias herramientas permiten especificar una relación espacial definiendo primero una estructura de vecindad (como una banda de distancia o los k vecinos más cercanos) y, a continuación, especificando un método para aplicar ponderaciones a los vecinos. De forma similar a la ponderación por distancia inversa, es común asignar mayores ponderaciones a los vecinos cercanos a la entidad focal utilizando una función, denominada kernel, que disminuye con la distancia. La ponderación kernel tiene la ventaja de proporcionar ponderaciones estables a los vecinos tanto a distancias cercanas como lejanas, mientras que la ponderación por distancia inversa presenta problemas en distancias menores a uno, y las ponderaciones disminuyen rápidamente al alejarse de la entidad focal. Todos los kernel utilizan un ancho de banda que puede ser fijo o adaptativo y que define la rapidez con la que las ponderaciones disminuyen con la distancia. Los kernels comunes incluyen el bicuadrado, gaussiano, triangular y cuadrático. Consulte Cómo funciona Estadísticas de resumen de vecindad para obtener más información sobre la ponderación de kernel.
La herramienta Generar matriz de ponderaciones espaciales también permite ponderar por la longitud del borde compartido al definir relaciones espaciales mediante contigüidad de polígonos. Esto permite asignar más influencia a entidades que comparten una parte más grande del borde de las entidades focales. También puede ponderar por valores de un campo, como población o área de polígono, para asignar ponderaciones más altas a las entidades con valores de campo más elevados. Al ponderar por borde compartido o valores de campo, todas las ponderaciones serían estandarizar por fila.
Método de distancia
Varias herramientas le brindan la opción de la distancia euclidiana o de Manhattan.
- La distancia euclidiana se calcula como
D = raíz cuadrada de [(x1–x2)**2,0 + (y1–y2)**2,0]donde (x1, y1) es la coordenada para el punto A, (x2, y2) es la coordenada para el punto B, y D es la distancia en línea recta entre los puntos A y B.
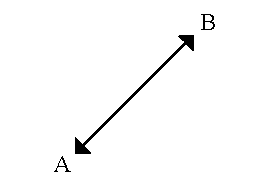
- La distancia de Manhattan se calcula como
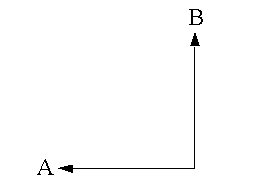
D = abs(x1–x2) + abs(y1–y2)donde (x1, y1) es la coordenada para el punto A, (x2, y2) es la coordenada para el punto B y D es la diferencia vertical más horizontal entre los puntos A y B. Es la distancia que debe desplazarse únicamente si tiene restricción para viajar norte-sur y este-oeste. Este método por lo general es más apropiado que la distancia euclidiana cuando el recorrido se limita a una red de calles y donde los costes de viaje de la red de calles real no están disponibles.
Cuando sus entidades de entrada no están proyectadas (es decir, las coordenadas son latitud y longitud) o cuando el sistema de coordenadas de salida se establece en un sistema de coordenadas geográficas, las distancias se calcularán mediante medidas de cuerda y el parámetro Método de distancia se deshabilitará. Las mediciones de distancia de cuerda se utilizan porque se pueden calcular rápidamente y proporcionan estimaciones precisas de las verdaderas distancias geodésicas, al menos para los puntos separados un máximo de unos treinta grados entre sí. Las distancias de cuerda se basan en un modelo esférico de la Tierra y, dados dos puntos cualesquiera en la superficie, la distancia de cuerda entre ellos es la distancia recta tridimensional que los conecta (esta línea recta atravesará la Tierra). Las distancias de cuerda se informan en metros.
Precaución:
Se recomienda proyectar los datos si el área de estudio se extiende más allá de 30 grados. Las distancias de cuerda no son una estimación fiable de las distancias geodésicas más allá de 30 grados.
Autoponderación
Varias herramientas permiten definir entidades y ponderaciones como vecinos de sí mismos; esto se denomina autoponderación. Por ejemplo, podría utilizar la autoponderación para reflejar los costes de viaje intrazonales promedio basados en el tamaño del polígono. La herramienta Análisis de puntos calientes permite proporcionar un campo que represente las autoponderaciones en el parámetro Campo auto potencial. Las herramientas Generar ponderaciones espaciales de red y Estadísticas de resumen de vecindad permiten incluir autoponderaciones mediante el parámetro Incluir entidad focal. Varias otras herramientas, como Asociación espacial bivariada (L de Lee), agregarán automáticamente autoponderaciones a cualquier relación espacial proporcionada.
Estandarizar filas
Se recomienda la estandarización de filas siempre que la distribución de las entidades esté potencialmente influenciada debido al diseño de muestreo o a un esquema de agregación impuesto. Cuando se selecciona la estandarización de filas, cada ponderación se divide por la suma de las filas (la suma de los pesos de todas las entidades vecinas) para que las ponderaciones sumen 1. La ponderación estandarizada por filas se utiliza a menudo con vecindades de distancia fija y casi siempre con vecindades basadas en contigüidad de polígonos. Esto sirve para mitigar la influencia debido a las entidades que tienen distintas cantidades de vecinos. La estandarización por filas crea un esquema de ponderación relativo, en lugar de absoluto, que resulta apropiado, por ejemplo, al trabajar con límites administrativos.
Banda de distancia
El parámetro Banda de distancia (a veces denominado distancia de umbral) establece la escala de análisis para la mayoría de las relaciones de espaciales de varias relaciones espaciales. Elegir una distancia apropiada es importante. Algunas estadísticas espaciales requieren que cada entidad tenga al menos un vecino para que el análisis sea confiable. Si la banda de distancia es demasiado pequeña (de manera que algunas entidades no tienen vecinos), aparece un mensaje de advertencia. La herramienta Calcular banda de distancia a partir de recuento de vecindad evaluará las distancias mínimas, promedio y máximas para un número de vecinos especificado y puede ayudarle a determinar un valor de banda de distancia apropiada para utilizar para el análisis. Para obtener pautas adicionales, consulte también Mejores prácticas para seleccionar un valor de banda de distancia fija.
Cuando no se especifica ningún valor, se calcula una distancia de umbral predeterminada. En la tabla a continuación se indica cómo se comportan las distintas relaciones espaciales para cada uno de los tres tipos de entradas posibles (los valores negativos no son válidos):
| Distancia inversa, distancia inversa cuadrada | Banda de distancia fija, zona de indiferencia | Contigüidad de polígono, triangulación de Delaunay, K vecinos más próximos | |
|---|---|---|---|
| 0 | No se aplica umbral ni valor límite; cada entidad es vecina de otra entidad. | No válido. Se generará un error de tiempo de ejecución. | Ignorado |
| vacío | Se calcula una distancia predeterminada. Este valor predeterminado será la distancia mínima para garantizar que cada entidad tenga al menos un vecino. | Se calcula una distancia predeterminada. Este valor predeterminado será la distancia mínima para garantizar que cada entidad tenga al menos un vecino. | Ignorado |
| número positivo | El valor positivo especificado que no equivale a cero se utilizará como una distancia de valor límite; las relaciones de vecino solo existirán entre las entidades dentro de esta distancia de una a otra. | Para la banda de distancia fija, solo las entidades que estén dentro de este valor límite especificado entre sí serán vecinas. Para la zona de indiferencia, las entidades dentro de este valor límite especificado entre sí serán vecinas; las entidades fuera del valor límite también serán vecinas, pero se les asignará un peso o influencia menor a medida que aumente la distancia. | Ignorado |
Cantidad de vecinos
El parámetro Cantidad de vecinos cumple una función en varias relaciones espaciales. Para los k vecinos más cercanos, cada entidad de destino utilizará las K entidades más próximas (donde K es el número de vecinos especificado). Para distancia inversa y banda de distancia, la distancia de umbral se ampliará para la entidad a fin de garantizar que tenga al menos K entidades. Para las relaciones espaciales de contigüidad de polígonos, se agregarán vecinos adicionales en función de la proximidad del centroide de la entidad para garantizar al menos K vecinos.
Archivo de texto de matriz de ponderaciones
Varias herramientas le permiten definir relaciones espaciales entre las entidades al proporcionar un archivo de matriz de ponderaciones espaciales (.swm). Las ponderaciones espaciales son números entre 0 y 1 que reflejan la interacción entre cada entidad y las demás entidades en el dataset. El archivo de matriz de ponderaciones espaciales se puede crear mediante la herramienta Generar matriz de ponderaciones espaciales o puede ser un simple archivo ASCII.
Cuando el archivo de matriz de ponderaciones espaciales es un simple archivo de texto ASCII, la primera línea debe ser el nombre de un campo de Id. único. Esto le brinda la flexibilidad para utilizar cualquier campo numérico en su dataset como el Id. al generar este archivo; sin embargo, el campo de Id. debe ser tipo Entero (largo o corto) y debe tener valores únicos para cada entidad. Después de la primera línea, se debe dar formato al archivo de ponderaciones espaciales en las tres columnas siguientes:
- Desde ID de entidad
- Hasta ID de entidad
- Ponderación
Por ejemplo, supongamos que tiene tres gasolineras. El campo que utiliza como campo de Id. se llama StationID y los Id. de las entidades son 1, 2 y 3. Debe modelar las relaciones espaciales entre estas tres gasolineras usando el tiempo de viaje inverso. El archivo ASCII puede tener el siguiente aspecto:

Escribir manualmente los valores correspondientes al archivo de matriz de ponderaciones espaciales puede resultar tedioso. Utilizar la herramienta Generar matriz de ponderaciones espaciales puede resultar más eficaz a la hora de crear un archivo de matriz de ponderaciones espaciales.
Archivo de matriz de ponderaciones espaciales (.swm)
La herramienta Generar matriz de ponderaciones espaciales creará un archivo de matriz de ponderaciones espaciales (.swm) que define las relaciones espaciales entre todas las entidades del dataset basándose en los parámetros que especifique. Este archivo se crea en formato de archivo binario de modo que los valores en el archivo no puedan verse directamente. Para ver o editar las relaciones de entidades en un archivo .swm, utilice la herramienta Convertir matriz de ponderaciones espaciales a tabla.
También puede utilizar la herramienta Generar matriz de ponderaciones espaciales para volver a convertir la tabla en un archivo .swm. La tabla requiere los campos siguientes:
| Nombre de campo | Descripción |
|---|---|
| <Nombre de campo de Id. único> | Un campo de entero único para cada entidad. El nombre y el tipo de campo deben coincidir con el campo de Id. único asociado de las entidades. Por ejemplo, si una entidad con Id. 6 tiene cuatro vecinos, el valor 6 se repetirá cuatro veces en este campo, una por cada vecino. |
| NID | Un campo de entero que contenga el Id. del vecino. |
| WEIGHT | Un peso numérico entre 0 y 1 que represente la influencia o la interacción entre dos entidades. |
La forma más sencilla de editar un archivo .swm con ponderaciones personalizadas consiste en crear un archivo .swm inicial y convertirlo en una tabla. Esta tabla tiene los nombres y las propiedades de campo correctos, por lo que puede crear y editar filas para asignar ponderaciones y relaciones de vecinos personalizadas. La tabla también debe estar ordenada por Id. único y luego por Id. de vecino.
Compartir archivos de matriz de ponderaciones espaciales
La salida de la herramienta Generar matriz de ponderaciones espaciales es un archivo .swm. Este archivo se vincula a la configuración de la clase de entidad de entrada, del campo de Id. único y del sistema de coordenadas de salida cuando se crea el archivo .swm. Otras personas pueden duplicar las relaciones espaciales que define para el análisis utilizando el archivo .swm y la misma clase de entidad de entrada, una clase de entidad que conecte todo o un subconjunto de las entidades a un campo Unique ID que coincida. Especialmente si desea compartir sus archivos .swm con otros, evite utilizar un sistema de coordenadas de salida que difiera de la referencia espacial de las entidades originales. Se recomienda proyectar primero las entidades de entrada y crear el archivo de matriz de ponderaciones espaciales para la nueva referencia espacial.
Ponderaciones espaciales de red
En algunos análisis, las relaciones espaciales se definen mejor por la distancia de viaje a lo largo de una red que atendiendo a la proximidad en línea recta. Por ejemplo, al modelar los tiempos de respuesta a emergencias, puede ser más apropiado definir a los vecinos en función del tiempo de recorrido por la ruta más corta de una red vial en lugar de la distancia euclidiana. Para datasets como este, puede usar la herramienta Generar ponderaciones espaciales de red para definir relaciones espaciales mediante un dataset de red, que define las relaciones espaciales en términos de la estructura de red subyacente.