Cómo funciona Evaluar la sensibilidad a la incertidumbre de los atributos

La herramienta Evaluar la sensibilidad a la incertidumbre de los atributos permite evaluar cómo cambian los resultados de análisis de las herramientas de selección de la caja de herramientas Estadísticas espaciales cuando una o varias variables de análisis (atributos) son inestables. Se puede especificar la incertidumbre de los atributos mediante el uso de márgenes de error, límites superior e inferior o un porcentaje determinado del valor original. Esta herramienta acepta las entidades de salida de las herramientas siguientes:

• Análisis de puntos calientes (Gi* de Getis-Ord)
• Análisis de puntos calientes optimizado
• Análisis de clúster y de valor atípico (I Anselin local de Moran)
• Análisis optimizado de valores atípicos
• Regresión lineal generalizada
• Autocorrelación espacial (I de Moran global)

La herramienta realiza un análisis de sensibilidad simulando repetidamente nuevos datos utilizando la variable de análisis original y su medida de incertidumbre. A continuación, vuelve a ejecutar varias veces la herramienta de análisis original utilizando los datos simulados y resume los resultados. Si los resultados de las simulaciones se parecen mucho a los resultados originales, esto le da confianza en que los resultados originales son sólidos y fiables. Sin embargo, si las simulaciones producen grandes diferencias con respecto a los resultados originales, debería dudar más a la hora de sacar conclusiones sólidas a partir de los resultados originales.

Potenciales aplicaciones

Las posibles aplicaciones de la herramienta incluyen las siguientes:

• Una organización benéfica local utiliza el análisis de puntos calientes para priorizar las áreas del condado en las que prestar servicios para paliar la pobreza. Tienen previsto centrarse en regiones en las que el análisis indique un nivel y una concentración elevados de pobreza (puntos calientes con un 99 % de confianza). Monitorizar cómo cambian los puntos conflictivos puede llevar a reforzar o reconsiderar las prioridades del servicio.
• Una gran cadena minorista ha desarrollado un modelo de regresión lineal generalizado para estimar cómo influyen factores demográficos como la edad y la renta disponible en la venta de artículos deportivos. Las variables explicativas recopiladas por medio de encuestas incluyen los límites superior e inferior. Al incorporar la incertidumbre en estas variables, el minorista puede examinar el rango potencial de volumen de ventas.

Incertidumbre de los atributos

La incertidumbre de los atributos es la variabilidad de los valores de datos que surgen de aspectos naturales o evitables de la recopilación e incorporación de datos, como los errores de muestreo o medición. Los errores de muestreo se producen cuando el dato se recopila en un subconjunto de población, planteando preguntas sobre lo bien que representa la muestra la población entera. El error de medición se produce cuando un instrumento de recopilación de datos, como un termómetro o un medidor de viento, introduce variaciones menores en los valores registrados en comparación con los valores verdaderos. Los datos suelen proporcionarse con la mejor estimación del valor verdadero de la medición, denominada estimación de punto, y alguna medida de su nivel de incertidumbre. Aunque estas fuentes de incertidumbre pueden afectar a la precisión de los datos, están presentes en el proceso de recopilación de datos del mundo real. Reconocer y explorar la incertidumbre de los atributos y su impacto en los resultados del análisis puede ayudar a hacer que los análisis sean más transparentes y sólidos.

Cómo se cuantifica la incertidumbre

Esta herramienta admite tres formas de especificar la incertidumbre de los atributos: margen de error, límites superior e inferior y porcentaje superior e inferior del valor de atributo.

Margen de error

El margen de error representa el rango en el que, con toda probabilidad, se encontrará el valor verdadero del atributo. Se asocia con un nivel de confianza (como el 90 por ciento), lo que indica lo seguro puede estar de que el valor real del atributo se encuentre en el rango definido en la estimación, más o menos el margen de error. Por ejemplo, en una encuesta se puede estimar que un condado tiene 2500 personas pobres, con un margen de error de 300 y un nivel de confianza del 90 por ciento. Esto significa que puede estar seguro al 90 por ciento de que el número verdadero de personas pobres está comprendido entre 2200 y 2800. Al utilizar este método, se necesita un campo de margen de error para una variable de análisis como mínimo. Este campo contiene el límite de error numérico que representa cuánto por encima o por debajo de la estimación de muestra se espera que esté el valor de población verdadero. El nivel de confianza es el 90 por ciento de manera predeterminada y puede ajustarse con el parámetro Nivel confianza del margen de error.

Nota:

Los márgenes de error suelen registrarse como campos junto con la variable original. Esto ocurre con muchas variables de los datos ArcGIS Living Atlas of the World procedentes del American Community Survey (ACS) de la Oficina del Censo de EE. UU. Muchas organizaciones nacionales de estadística proporcionan medidas similares de incertidumbre.

Límites superior e inferior

Los límites superior e inferior representan la incertidumbre de un atributo al especificar de manera explícita un rango en torno a una estimación. A diferencia del margen de error, los límites superior e inferior no tienen que ser simétricos respecto a la estimación de punto.

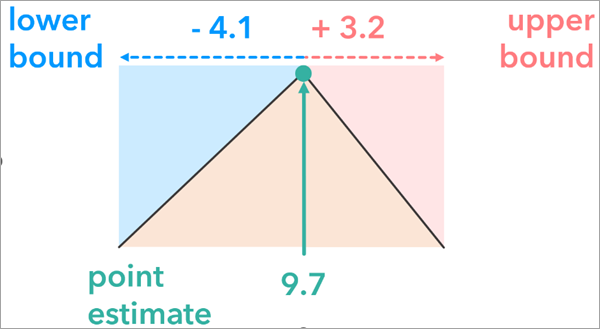
Porcentajes superior e inferior

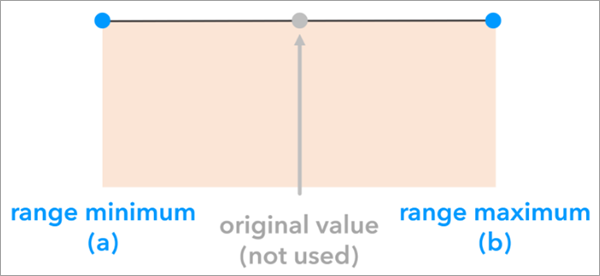
La opción de porcentaje superior e inferior representa la incertidumbre de los atributos al ajustar el valor de atributo original de cada entidad según un porcentaje especificado. Esto crea un rango con respecto a la estimación que podría contener el valor verdadero. Este método puede resultar útil cuando no hay otros métodos disponibles, como el margen de error o los límites superior e inferior, para expresar la incertidumbre.

Nota:

A diferencia de las opciones de margen de error y límite superior e inferior, que permiten especificar la incertidumbre de los atributos de manera diferente para cada entidad, el porcentaje superior y el porcentaje inferior aplican la misma definición de incertidumbre a todas las entidades.

Uso de simulaciones para resolver la incertidumbre

Para evaluar la propensión de los resultados del análisis a la incertidumbre, la herramienta genera datasets simulados basados en la variable de análisis original y su medida de incertidumbre. Lo ideal es que cada dataset simulado represente una versión Además, existen diferentes supuestos con respecto a cómo podrían centrarse o alejarse el valor verdadero con respecto a la estimación de punto. La herramienta utiliza las distribuciones de probabilidad para restringir los valores de datos simulados con el fin de capturar el rango y la probabilidad de realizaciones diferentes de los datos. Se admiten tres distribuciones: normal, triangular y uniforme. Al simular datos para la Regresión lineal generalizada, se mantiene la estructura de correlación entre las variables explicativas. Para los resultados de análisis de otras herramientas, los datos se simulan independientemente de cada entidad. Para tener en cuenta la dependencia entre las variables explicativas, su correlación se estima globalmente y los valores simulados de cada entidad se generan agregando ruido aleatorio de una distribución normal multivariante con media cero y matriz de covarianza basada en la correlación global entre las variables explicativas. Como el ruido aleatorio se basa en una distribución normal multivariante, las simulaciones para la Regresión lineal generalizada solo admiten el método de simulación normal.

Normal

La opción Normal del parámetro Método de simulación suele utilizarse cuando hay disponible un margen de error con un nivel de confianza asociado. Esta opción emplea una distribución de probabilidad normal (o gaussiana) con una media equivalente al valor de la variable de análisis original y una desviación estándar basada en el nivel de confianza y el valor de margen de error de la entidad.

Como sugiere la forma de la distribución de probabilidad, los valores más parecidos a la estimación original tienen más probabilidad de generarse que los más diferentes. Sin embargo, esto puede variar de manera considerable dependiendo del margen de error. Las ubicaciones con márgenes de error mayores, a menudo debido a tamaños de muestra menores, tendrán distribuciones con colas más largas, lo que implica una mayor probabilidad de que las simulaciones generen valores más apartados de la estimación original.

Triangular

La distribución triangular suele utilizarse cuando el valor original representa una estimación probable del valor verdadero. La opción Triangular del parámetro Método de simulación resulta particularmente útil con distribuciones asimétricas en las que es más probable que los valores se agrupen en torno al valor estimado, pero con una distribución asimétrica. La distribución triangular se crea y utiliza para simular los datos de cada entidad a partir del valor de datos mínimo, el valor original de la entidad y el valor de datos máximo. El valor del parámetro Tipo de incertidumbre determina los valores de datos máximo y mínimo de la distribución triangular.

La forma de la distribución de probabilidad triangular asegura que los valores parecidos al valor original tienen más probabilidad de generarse que los valores de los extremos de la distribución.

Nota:

A diferencia de la distribución normal, no es necesario que la forma sea simétrica. Por ejemplo, el límite inferior y superior pueden diferir.

Uniforme

La opción Uniforme del parámetro Método de simulación se emplea cuando el valor original en cada ubicación es una estimación inexacta del valor verdadero y la única información disponible sobre la incertidumbre de los atributos es el rango de valores posibles. Esta opción utiliza una distribución de probabilidad uniforme con dos parámetros: el mínimo en el rango establecido por el tipo de incertidumbre y el máximo en el rango establecido por el tipo de incertidumbre. A diferencia de las distribuciones normal y triangular, la distribución uniforme no utiliza el valor original en los parámetros de distribución de probabilidad; todos los valores entre el mínimo y el máximo tienen la misma probabilidad de generarse en las simulaciones.

Herramientas compatibles

A diferencia de la mayoría de herramientas de geoprocesamiento que aceptan una capa existente como entrada, la entrada de esta herramienta es la capa de resultados de una de las siguientes herramientas de la caja de herramientas Estadística espacial.

• Análisis de puntos calientes (Gi* de Getis-Ord)
• Análisis de puntos calientes optimizado
• Análisis de clúster y de valor atípico (I Anselin local de Moran)
• Análisis optimizado de valores atípicos
• Regresión lineal generalizada
• Autocorrelación espacial (I de Moran global)

Herramientas Análisis de puntos calientes, Análisis de puntos calientes optimizado, Análisis de clúster y de valor atípico y Análisis optimizado de valores atípicos

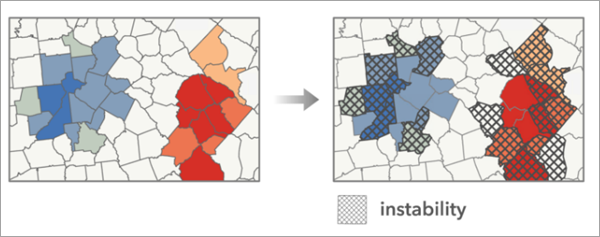
En el caso de los resultados de las herramientas Análisis de puntos calientes (Gi* de Getis-Ord), Análisis de puntos calientes optimizado, Análisis de cluster y de valor atípico (I Anselin local de Moran) y Análisis optimizado de valores atípicos, la estabilidad se evalúa mediante la determinación de la frecuencia con que una entidad cambia de categoría en las ejecuciones repetidas del análisis. Por ejemplo, si una entidad era un punto caliente con el 90 por ciento de confianza en el análisis original y cambió a otra categoría en una de las ejecuciones con datos simulados, se considera como un cambio de categoría. La herramienta cuenta la cantidad de veces que una entidad cambia de categoría. Las entidades se marcan como inestables cuando menos del 80 por ciento de las simulaciones resulta en la categoría original.

La herramienta produce una capa de grupo que contiene una capa de inestabilidad y una copia de los resultados del análisis original.

Asimismo, la capa de grupo contiene un gráfico que muestra el número de entidades de cada categoría de análisis original y cada categoría predominante. La categoría predominante es la más frecuente en todas las ejecuciones repetidas de la herramienta en cada ubicación.

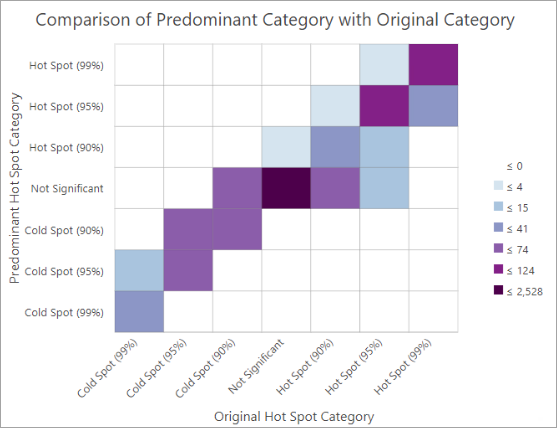
Este gráfico puede ayudar a identificar los patrones de inestabilidad categóricos. Un resultado perfectamente estable en el que cada categoría original se corresponde a la perfección con la categoría predominante rellenaría las diagonales de celda.

Nota:

La herramienta no admite los resultados del análisis de datos de puntos agregados cuando se ejecuta la herramienta Análisis de puntos calientes optimizado y Análisis optimizado de valores atípicos.

Herramienta Regresión lineal generalizada

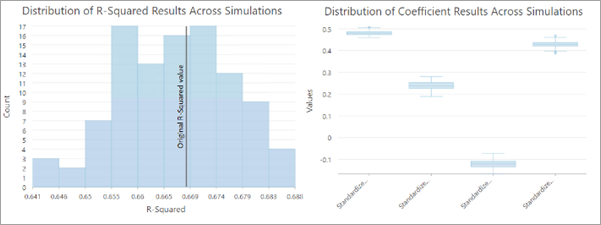
Al evaluar la incertidumbre de un análisis de regresión lineal generalizada, los resultados principales de la herramienta Regresión lineal generalizada son gráficos en los que se muestra la distribución de los diagnósticos de regresión entre ejecuciones simuladas, como R cuadrado y coeficientes de variable explicativa. La herramienta proporciona una capa de grupo que contiene una copia del resultado del análisis original, una tabla en la que se resumen los resultados de las ejecuciones repetidas de la herramienta original y tres gráficos que muestran la distribución de la relevancia estadística de Jarque-Bera y R cuadrado, además de los coeficientes de variables explicativas estandarizados.

Herramienta Autocorrelación espacial (I de Moran)

En el caso de los resultados de la herramienta Autocorrelación espacial (I de Moran global), el objetivo de la herramienta es ayudarle a conocer la certeza de la evaluación original de la autocorrelación espacial global según la incertidumbre de los atributos. La herramienta proporciona una capa de grupo con una copia del resultado del análisis original, una tabla en la que se resumen los resultados de las ejecuciones repetidas de la herramienta y gráficos que muestran la distribución de los valores del índice de Moran y su puntuación z.

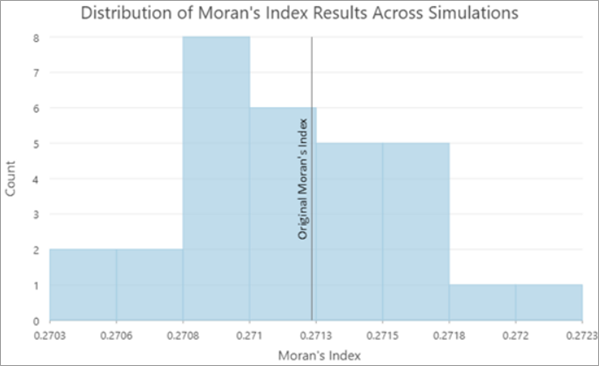
Por lo general, la mayoría de los valores del índice de Moran y sus puntuaciones z serán menores que los valores originales, ya que la agregación de ruido aleatorio no correlacionado a los valores de los datos tiende a reducir la autocorrelación espacial de los datos.

Nota:

La herramienta Autocorrelación espacial (I de Moran global) no genera entidades de salida. Utilice las entidades de salida originales que se emplearon en el análisis de Autocorrelación espacial (I de Moran global) como valor del parámetro Entidades de resultados de análisis.

Consideraciones adicionales

Las subsecciones siguientes proporcionan información adicional.

Modificar el umbral de estabilidad en la salida

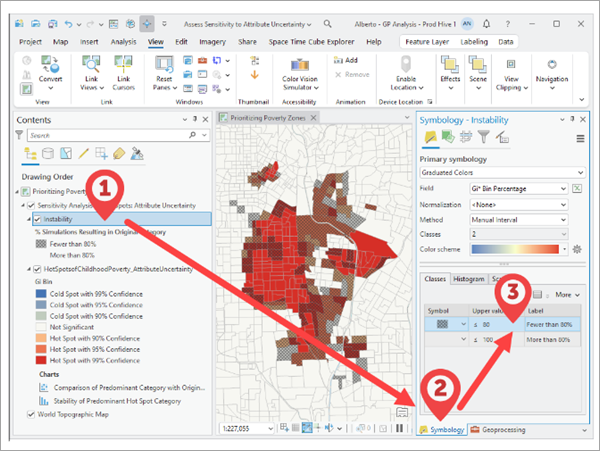
En el caso de los resultados de las herramientas Análisis de puntos calientes (Gi* de Getis-Ord), Análisis de puntos calientes optimizado, Análisis de cluster y de valor atípico (I Anselin local de Moran) y Análisis optimizado de valores atípicos, la capa de inestabilidad aplica un umbral de estabilidad predeterminado del 80 por ciento. Esto significa que para que una entidad se considere estable, la entidad debe resultar en la misma categoría que el análisis original en más del 80 por ciento de las simulaciones. El aumento de este umbral designará un mayor número de entidades como inestables, y la disminución de este umbral designará menos entidades como inestables.

El umbral que define la estabilidad puede configurarse utilizando los valores de la simbología de capa. Para cambiar el umbral, primero debe encontrar y seleccionar la capa de inestabilidad en la capa de grupo de salida. En segundo lugar, abra el panel Simbología y, en tercer lugar, haga doble clic en la celda del valor Superior correspondiente a la clase del 80 por ciento y edite el valor de umbral.

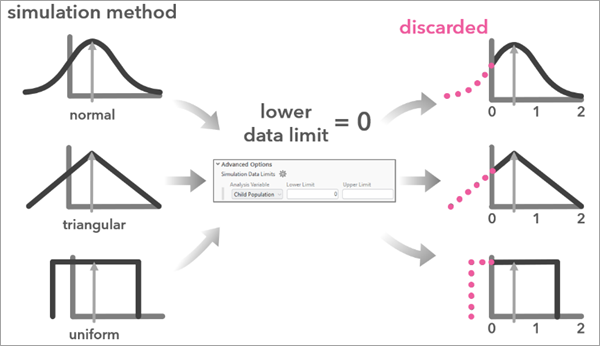
Límites de datos de simulación

Puede establecer los límites en el rango de valores simulados de una variable de análisis. Esto puede resultar útil cuando la variable de análisis debería ser negativa (recuentos) o debería tener un rango entre cero y 100 (porcentajes). Utilice el parámetro Límites de datos de simulación para configurar el rango de posibles valores de cada variable. Cuando se especifica el valor del parámetro Límite de datos de simulación, la herramienta descarta los valores simulados que quedan fuera del rango especificado y repite la simulación.

Guardar los resultados de simulación intermedios

Las simulaciones que crea la herramienta pueden guardarse como clases de entidad. Utilice el parámetro Espacio de trabajo de resultados de simulación para configurar un espacio de trabajo existente en el que la herramienta guardará cada resultado de simulación.

La convención de nomenclatura de cada archivo respeta el formato siguiente: nombre de entidades de resultado de análisis _ Id. de simulación _ Maca de tiempo de simulación. Cada clase de entidad de resultado de simulación contiene el esquema del resultado del análisis original.

Los resultados de simulación intermedios podrían ser útiles en otros análisis. Por ejemplo, podría examinar un espacio de trabajo de la herramienta de resultados de simulación de Regresión lineal generalizada para entender mejor la distribución de los valores pronosticados en las simulaciones.

Metadatos de operaciones de geoprocesamiento

Para encontrar la herramienta de análisis, las entidades de entrada y los parámetros adicionales empleados en el análisis, la herramienta lee los metadatos del valor del parámetro Entidades de resultados de análisis. Por consiguiente, el análisis que produjo las entidades del resultado del análisis debe configurarse para escribir en metadatos.

Esta configuración está activada de manera predeterminada. Para confirmar esta configuración, abra el cuadro de diálogo Opciones, haga clic en la pestaña Geoprocesamiento, y en la sección Registrar, verifique que la opción Escribir las operaciones de geoprocesamiento en los metadatos del dataset está activada.

Nota:

La herramienta no admite la ejecución de análisis de la herramienta Autocorrelación espacial (I de Moran global) en capas alojadas, puesto que los metadatos de estos datasets no se pueden modificar.

Recursos adicionales

Para obtener más información, consulte los recursos siguientes:

• JingXiong Zhang y Michael Goodchild. 2002. "Uncertainty in Geographical Information." Taylor & Francis. ISBN 0-203-47132-6. https://doi.org/10.1201/b12624.
• Raphaella Diniz, Pedro O.S. Vaz-de-Melo, Renato Assunção. 2024. “Data augmentation for spatial disease mapping.” Spatial Data Science Symposium 2021 Short Paper Proceedings. https://doi.org/10.25436/E2KS35
• Michele Crosetto y Stefano Tarantola. 2001. "Uncertainty and sensitivity analysis: tools for GIS-based model implementation." International Journal of Geographical Information Science. 15:5, 415-437. https://doi.org/10.1080/13658810110053125
• Zhou Dimin. 2010. “Research on Propagation of Attribute Uncertainty in GIS.” 2010 International Conference on Intelligent Computation Technology and Automation.
• Hyeongmo Koo, Takuya Iwanaga, Barry F.W. Croke, Anthony J. Jakeman, Jing Yang, Hsiao-Hsuan Wang, Xifu Sun, Guonian Lü, Xin Li, Tianxiang Yue, Wenping Yuan, Xintao Liu y Min Chen. 2020. “Position paper: Sensitivity analysis of spatially distributed environmental models- a pragmatic framework for the exploration of uncertainty sources.” Environmental Modelling and Software. https://doi.org/10.1016/j.envsoft.2020.104857
• Hyeongmo Koo , Yongwan Chun y Daniel A. Griffith. 2018. “Geovisualizing attribute uncertainty of interval and ratio variables: A framework and an implementation for vector data.” Journal of Visual Languages and Computing 44 89-96. https://doi.org/10.1016/j.jvlc.2017.11.007
• Robert Haining, Daniel A. Grifith y Robert Bennett. 1983. “Simulating Two-dimensional Autocorrelated Surfaces.” Geographical Analysis. https://doi.org/10.1111/j.1538-4632.1983.tb00785.x
• Sirius Fuller y Charles Gamble. 2020. "Calculating Margins of Error the ACS Way." American Community Survey (ACS) Programs and Surveys, U.S. Census Bureau.
• Shuliang Wang, Wenzhong Shi, Hanning Yuan y Guoqing Chen. 2005. "Attribute Uncertainty in GIS Data". Fuzzy Systems and Knowledge Discvery Conference. 3614, 614-623. https://doi.org/10.1007/11540007_76
• Ningchuan Xiao, Catherine A. Calder y Marc P. Armstrong. 2007. "Assessing the effect of attribute uncertainty on the robustness of choropleth mapclassification." International Journal of Geographical Information Science. 21:2, 121-144. https://doi.org/10.1080/13658810600894307