L’analyse de régression est peut-être la statistique la plus couramment utilisée en sciences sociales. La régression permet d’évaluer les relations entre deux attributs d’entités ou plus. L’identification et la mesure des relations permettent de mieux comprendre ce qui se passe dans un endroit, de prévoir où un autre événement est susceptible de survenir ou d’examiner les origines de tel ou tel événement.
La régression par la méthode des moindres carrés ordinaires est la technique de régression la plus connue. C’est également le point de départ de toutes les analyses de régression spatiales. Il offre aussi un modèle global de la variable ou du processus que vous tentez de comprendre ou de prévoir. Il crée une équation de régression unique qui représente ce processus.
Il existe de nombreuses ressources utiles qui vous aideront à approfondir vos connaissances sur la régression des moindres carrés ordinaires et la régression pondérée géographiquement. Commencez par lire la rubrique Principes de base de l’analyse de régression. Ensuite, exercez-vous avec le didacticiel Regression Analysis. Cette rubrique traite les résultats de votre analyse afin de vous aider à comprendre le résultat et les diagnostics de la méthode des moindres carrés ordinaires.
Entrée(s)
Pour exécuter l’outil Moindres carrés ordinaires, vous devez spécifier une Input Feature Class (Classe d’entités en entrée) avec un Unique ID Field (Champ d’identifiant unique), la Dependent Variable (Variable dépendante) que vous souhaitez modéliser, expliquer, prévoir, ainsi qu’une liste de Explanatory Variables (Variables explicatives). Vous devez également indiquer un chemin pour la Classe d'entités en sortie et, en option, les chemins du Fichier de rapport en sortie, de la Table en sortie des coefficients et de la Table en sortie des diagnostics.
Interprétation des résultats des moindres carrés ordinaires
La sortie générée à l’aide de l’outil Moindres carrés ordinaires inclut une classe d’entités en sortie symbolisée à l’aide des valeurs résiduelles des moindres carrés ordinaires, des résultats statistiques et des diagnostics dans la fenêtre Messages, ainsi que plusieurs sorties facultatives comme un fichier de rapport PDF, une table de coefficients de variables explicatives et une table de diagnostics de régression. Chacune de ces sorties est décrite ci-dessous sous forme de série d’étapes pour l’exécution de la régression des moindres carrés ordinaires et l’interprétation des résultats correspondants.
Après l’exécution de l’outil Moindres carrés ordinaires, vérifiez le rapport récapitulatif des moindres carrés ordinaires, disponible sous forme de messages au cours de l’exécution de l’outil et enregistré dans un fichier de rapport lorsque vous spécifiez un chemin d’accès pour le paramètre Output Report File (Fichier de rapport en sortie).
Examinez le rapport récapitulatif en suivant les instructions numérotées ci-dessous :
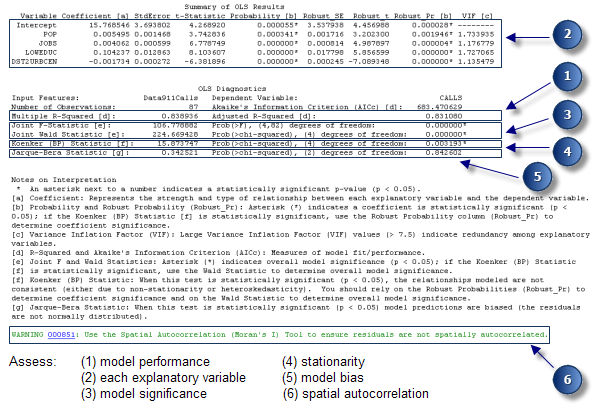
Évaluation du rapport statistique
- Evaluez la performance du modèle. Les deux valeurs R carré multiple et R carré ajusté sont des mesures des performances du modèle. Les valeurs possibles s'échelonnent de 0,0 à 1,0. La valeur R carré ajustée est toujours légèrement inférieure à la valeur R carré multiple, car elle reflète la complexité du modèle (nombre de variables) dans son lien aux données et représente par conséquent une mesure plus précise des performances du modèle. L’ajout au modèle d’une variable explicative augmentera probablement la valeur R-carré multiple, mais risque de réduire la valeur R-carré ajusté. Supposons que vous créez un modèle de régression du cambriolage résidentiel (le nombre de cambriolages résidentiels associé à chaque îlot de recensement est votre variable dépendante, y). Une valeur R carré ajustée de 0,39 indiquerait que votre modèle (vos variables explicatives modélisées à l'aide de la régression linéaire) explique approximativement 39 pour cent de la variation dans la variable dépendante. Autrement dit, votre modèle « explique » environ 39 pour cent du phénomène de cambriolage résidentiel.

Les valeurs R-carré quantifient les performances du modèle. - Evaluez chaque variable explicative du modèle : coefficient, probabilité ou probabilité robuste et facteur d'inflation de la variance (VIF). Le coefficient pour chaque variable explicative reflète à la fois la force et le type de la relation que la variable explicative présente avec la variable dépendante. Lorsque le signe associé au coefficient est négatif, la relation est négative (par exemple, plus le noyau urbain est éloigné, plus le nombre de cambriolages résidentiels est réduit). Lorsque le signe est positif, la relation est positive (par exemple, plus la population est importante, plus le nombre de cambriolages résidentiels est élevé). Les coefficients sont indiqués avec les mêmes unités que leurs variables explicatives associées (un coefficient de 0,005 associé à une variable représentant des décomptes de population peut être interprété en tant que 0,005 personnes). Le coefficient reflète la variation prévue de la variable dépendante pour toute variation d’une unité dans la variable explicative associée, toutes les autres variables restant constantes (par exemple, une augmentation de 0,005 du cambriolage résidentiel est prévue pour chaque personne supplémentaire dans l’îlot de recensement, toutes les autres variables explicatives restant constantes). Le test T permet d’évaluer si une variable explicative est statistiquement significative. L'hypothèse nulle est que le coefficient est en réalité égal à zéro (et par conséquent n'apporte rien au modèle). Lorsque la probabilité ou la probabilité robuste (valeur p) est très faible, la probabilité que le coefficient soit en fait égal à zéro est également faible. Si le test de Koenker (voir ci-dessous) est statistiquement significatif, utilisez les probabilités robustes pour évaluer la signification statistique de la variable explicative. Les probabilités statistiquement significatives portent un astérisque (*). Une variable explicative associée à un coefficient statistiquement significatif est importante pour le modèle de régression si la théorie ou le bon sens appuient une relation valide avec la variable dépendante si la relation modélisée est essentiellement linéaire, et si la variable n’est pas redondante par rapport à une autre variable explicative du modèle. La valeur VIF mesure la redondance entre les variables explicatives. En règle générale, les variables explicatives associées aux valeurs VIF supérieures à 7,5 doivent être supprimées (une par une) du modèle de régression. Si, par exemple, votre modèle de régression inclut une variable de population (nombre de personnes) et une variable d’emploi (nombre de personnes employées), elles sont probablement associées à des valeurs VIF élevées indiquant que ces deux variables expliquent le même phénomène. Vous devez supprimer l’une d’elles de votre modèle.
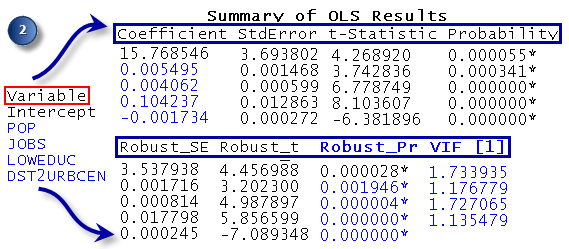
Evaluez quelles variables sont statistiquement significatives. - Evaluez la signification du modèle. Les deux valeurs Statistique F de jointure et Statistique Wald de jointure sont des mesures de la signification statistique globale du modèle. La Statistique F de jointure est digne de confiance uniquement lorsque la statistique Koenker (BP, voir ci-dessous) n'est pas statistiquement significative. Si la statistique Koenker (BP) est significative, vous devez consulter la Statistique Wald de jointure pour déterminer la signification globale du modèle. L’hypothèse nulle pour ces deux tests est que les variables explicatives dans le modèle ne sont pas efficaces. Pour un niveau de confiance de 95 pour cent, une valeur de p (probabilité) inférieure à 0,05 indique un modèle statistiquement significatif.
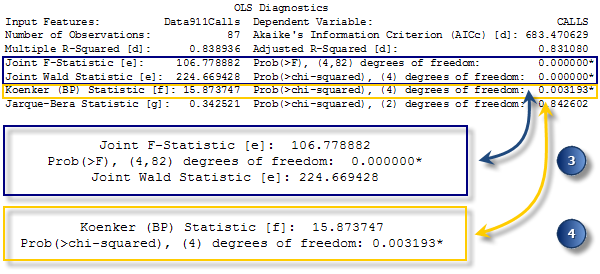
Evaluez la signification statistique globale du modèle de régression. - Évaluez la stationnarité. La statistique de Koenker (BP) (statistique Breusch-Pagan avec transformation de Student de Koenker) est un test permettant de déterminer si les variables explicatives du modèle ont une relation cohérente avec la variable dépendante à la fois dans l’espace géographique et dans l’espace de données. Lorsque le modèle est cohérent dans l'espace géographique, les processus spatiaux représentés par les variables explicatives se comportent de la même manière partout dans la zone d'étude (les processus sont stationnaires). Lorsque le modèle est cohérent dans l'espace de données, la variation dans la relation entre les valeurs de prévision et chaque variable explicative ne change pas avec les variations dans les grandeurs variables explicatives (absence de hétéroscédasticité dans le modèle). Supposons que vous souhaitez prédire les infractions et que l'une de vos variables explicatives est le revenu. Le modèle aurait une hétéroscédasticité problématique si les prévisions étaient plus précises pour les emplacements avec des revenus médians réduits que pour les emplacements avec des revenus médians élevés. L'hypothèse nulle pour ce test est que le modèle est stationnaire. Pour un niveau de confiance de 95 pour cent, une valeur de p (probabilité) inférieure à 0,05 indique une hétéroscédasticité et/ou absence de stationnarité statistiquement significative. Lorsque les résultats de ce test sont statistiquement significatifs, consultez les erreurs standard et les probabilités des coefficients robustes pour évaluer l'efficacité de chaque variable explicative. Les modèles de régression avec absence de stationnarité statistiquement significative sont souvent de bons candidats pour l'analyse Régression pondérée géographiquement.
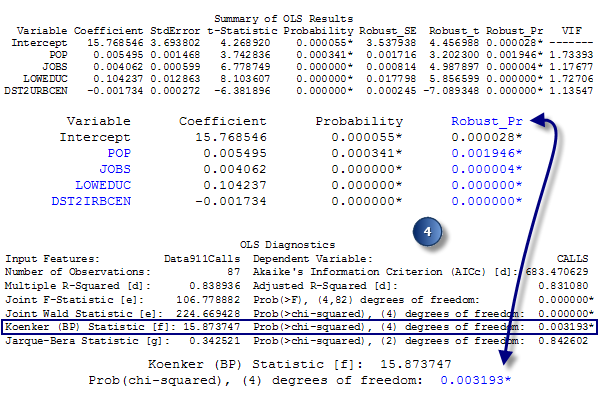
Évaluer la stationnarité : si le test de Koenker est statistiquement significatif (*), consultez les probabilités robustes pour déterminer si les coefficients des variables explicatives sont significatifs. - Evaluez le biais du modèle. La statistique Jarque-Bera indique si les valeurs résiduelles (les valeurs des variables dépendantes connues ou observées moins les valeurs prévues ou estimées) sont distribuées normalement. L'hypothèse nulle pour ce test est que les valeurs résiduelles sont distribuées normalement, donc si vous devez construire un histogramme à partir de ces valeurs résiduelles, il ressemblerait à une courbe en cloche classique, ou distribution gaussienne. Si la valeur p (probabilité) pour ce test est faible (inférieure à 0,05 pour un niveau de confiance de 95 pour cent, par exemple), les valeurs résiduelles ne sont pas distribuées normalement, ce qui indique que votre modèle est biaisé. Si l'autocorrélation spatiale des valeurs résiduelles de régression est statistiquement significative (voir ci-dessous), le biais peut provenir d'une spécification incorrecte du modèle (il lui manque une variable clé). Les résultats d'un modèle de moindres carrés ordinaires mal spécifié ne sont pas dignes de confiance. Un test de Jarque-Bera statistiquement significatif peut également se présenter si vous tentez de modéliser des relations non linéaires, si vos données incluent des points aberrants influents ou s’il existe une forte hétéroscédasticité.
Evaluez le biais du modèle. - Évaluez l’autocorrélation spatiale des valeurs résiduelles. Exécutez toujours l'outil Spatial Autocorrelation (Moran's I) sur les valeurs résiduelles de régression pour vous assurer qu'elles sont spatialement aléatoires. L’agrégation statistiquement significative de valeurs résiduelles élevées et faibles (surestimations et sous-estimations du modèle) indique qu’une variable essentielle manque dans le modèle (mauvaise spécification). Les résultats des moindres carrés ordinaires ne sont pas dignes de confiance lorsque le modèle est mal spécifié.

Utilisez l'outil Spatial Autocorrelation pour vous assurer que les valeurs résiduelles du modèle ne sont pas auto-corrélées spatialement. - Consultez la section Corruption des modèles de régression, dans la rubrique Principes de base de l’analyse de régression pour vous assurer que votre modèle de régression des moindres carrés ordinaires est correctement spécifié. Si vous avez des difficultés à trouver un modèle de régression correctement spécifié, l’outil Régression exploratoire peut se révéler utile. La section intitulée Notes sur l’interprétation à la fin du rapport récapitulatif des moindres carrés ordinaires a pour fonction de vous rappeler l’objectif de chaque test statistique et de vous aider à trouver une solution lorsque votre modèle échoue à des tests de diagnostic.

Le rapport des moindres carrés ordinaires comprend des notes pour vous aider à interpréter le diagnostic en sortie.
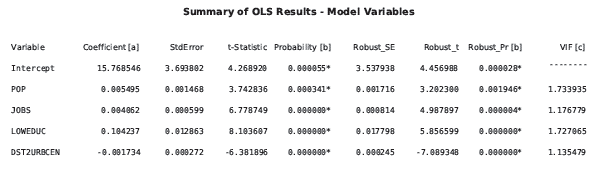
Si vous spécifiez un chemin pour le fichier de rapport en sortie facultatif, un fichier PDF est créé. Il contient toutes les informations du rapport récapitulatif ainsi que des graphiques supplémentaires vous permettant d’évaluer votre modèle. La première page du rapport donne des informations détaillées sur chaque variable explicative. À l’instar de la première section du rapport récapitulatif (voir l’étape 2 ci-dessus), les informations présentées ici vous permettent de déterminer si les coefficients de chaque variable explicative sont statistiquement significatifs et présentent le signe attendu (+/-). Si le test de Koenker est statistiquement significatif (voir l’étape 4 ci-dessus), seules les probabilités robustes vous permettront de déterminer si une variable est utile à votre modèle. Les coefficients statistiquement significatifs sont indiqués par un astérisque en regard de leur valeur p dans la colonne des probabilités et celle des probabilités robustes. Vous pouvez également déduire des informations données sur cette page du rapport si certaines de vos variables explicatives sont redondantes (si elles présentent une multicolinéarité problématique). Sauf si la théorie exige le contraire, vous devez supprimer une à une les variables explicatives dont la valeur de facteur d'inflation de la variance (VIF) est élevée, jusqu'à que la valeur VIF de chacune des variables explicatives restantes soit inférieure à 7,5.
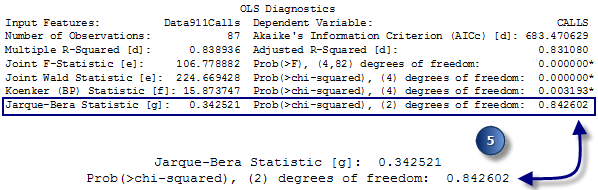
La section suivante du fichier de rapport en sortie dresse la liste des résultats des tests de diagnostic des moindres carrés ordinaires. Cette page inclut également une partie intitulée Notes sur l’interprétation décrivant l’importance de chaque test. Si votre modèle échoue à l'un de ces diagnostics, consultez la table des problèmes de régression courants pour obtenir des informations sur la sévérité de chaque problème ainsi que des solutions possibles. Les graphiques inclus dans les pages suivantes du rapport vous permettront également d'identifier et corriger les problèmes existant dans votre modèle.

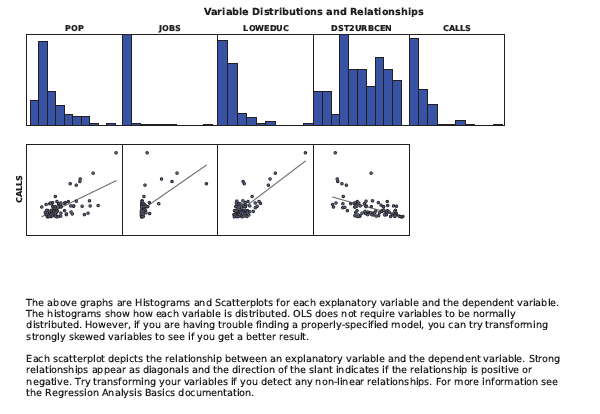
La troisième section du fichier de rapport en sortie inclut des histogrammes indiquant la distribution de chaque variable de votre modèle, et des nuages de points montrant la relation entre la variable dépendante et chaque variable explicative. Si votre modèle est biaisé (si la valeur p Jarque-Bera est statistiquement significative), recherchez les distributions asymétriques dans les histogrammes, et essayez de transformer ces variables pour vérifier si le biais est ainsi éliminé et les performances du modèle améliorées. Les nuages de points montrent quelles variables sont les meilleurs prédicteurs. Utilisez-les pour vérifier également l'existence éventuelle de relations non linéaires entre vos variables. Dans certains cas, la transformation d’une ou plusieurs variables permet de corriger les relations non linéaires et la déviation du modèle. La présence de points aberrants dans les données peut également résulter en un modèle biaisé. Vérifiez les histogrammes et les nuages de points pour ces valeurs de données et relations entre données. Exécutez le modèle avec et sans point aberrant pour voir dans quelle mesure il affecte vos résultats. Vous découvrirez peut-être que le point aberrant correspond à des données non valides (entrées ou enregistrées par erreur) et pourrez peut-être supprimer l'entité associée de votre jeu de données. Si le point aberrant représente des données valides et a un impact très fort sur les résultats de votre analyse, vous pouvez décider de produire un rapport des résultats obtenus avec et sans le point aberrant.
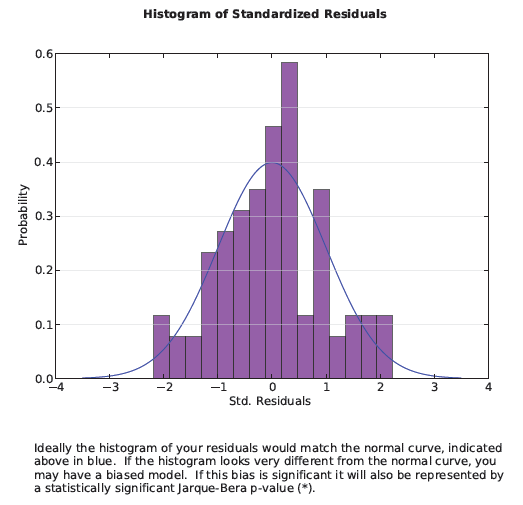
Si votre modèle est correctement spécifié, les sous-estimations et surestimations reflètent le bruit aléatoire. Si vous créez un histogramme de bruit aléatoire, il sera normalement distribué (imaginez une courbe en cloche). La quatrième section du fichier de rapport en sortie présente l’histogramme des sous-estimations et des surestimations du modèle. Les barres de l'histogramme représentent la distribution réelle, et la ligne bleue superposée sur l'histogramme montre la forme qu'aurait l'histogramme si vos valeurs résiduelles étaient normalement distribuées. Il est peu probable que l’histogramme soit parfait, nous vous invitons donc à vérifier les résultats du test de Jarque-Bera pour déterminer si l’écart par rapport à une distribution normale est statistiquement significatif.
Le test de Koenker indique si les relations que vous modélisez varient sur l'ensemble de la zone d'étude (non stationnarité) ou en fonction de la magnitude de la variable que vous essayez de prévoir (hétéroscédasticité). L’outil Régression pondérée géographiquement permet de résoudre les problèmes de non-stationnarité. Le graphique de la section 5 du fichier de rapport en sortie indique s’il existe un problème d’hétéroscédasticité. Ce graphique en nuages de points (voir ci-dessous) représente la relation entre les valeurs résiduelles du modèle et les valeurs prédites. Supposons que vous modélisiez des taux de criminalité. Si le graphique est de forme conique, avec la pointe sur le côté gauche du graphique et la partie la plus large sur le côté droit, votre modèle prédit correctement dans les zones à faible taux de criminalité, mais ne fonctionne pas correctement là où la criminalité est élevée.
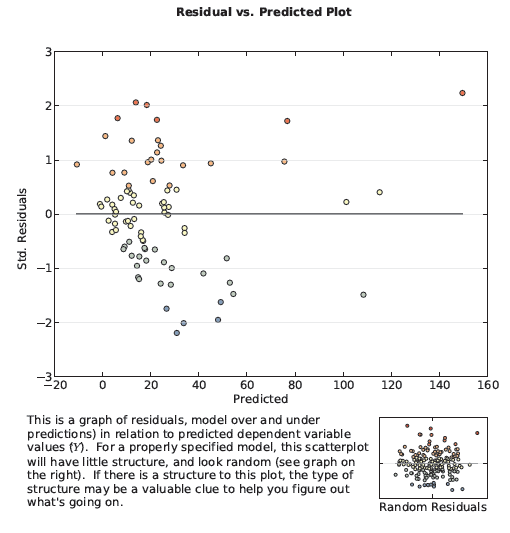
La dernière page du rapport indique toutes les valeurs de paramètres utilisées lors de sa création.
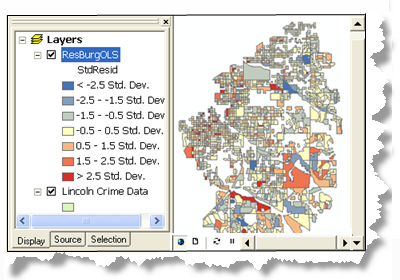
Étudiez les valeurs résiduelles du modèle présentes dans la Output Feature Class (Classe d’entités en sortie). Les sous-estimations et sur-estimations pour un modèle de régression correctement spécifié sont distribuées de manière aléatoire. Un regroupement de sous-estimations et de surestimations est la preuve qu’il manque au moins une variable explicative essentielle. Examinez les structures dans vos valeurs résiduelles du modèle pour voir si elles fournissent des indices sur les variables manquantes. L'exécution de l'outil Hot Spot Analysis sur les valeurs résiduelles de régression peut parfois permettre d'identifier des tendances plus larges. Vous trouverez des stratégies supplémentaires pour traiter un modèle incorrectement spécifié dans la rubrique Ce que l’on ne vous dit pas sur l’analyse de régression.
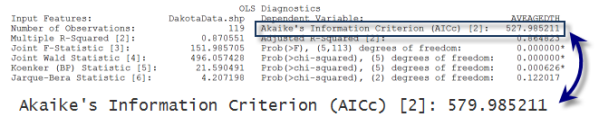
Consultez les tables des diagnostics et des coefficients. La création des tables des diagnostics et des coefficients est facultative. Vous pouvez choisir de ne pas créer ces tables pendant le processus de recherche d’un modèle efficace. Le processus de création de modèle est itératif, et vous allez vraisemblablement essayer plusieurs modèles différents (variables explicatives différentes) avant de vous décider pour quelques modèles adaptés. Vous pouvez utiliser le critère d’information Akaike corrigé (AICc) sur le rapport pour comparer différents modèles. Le modèle avec la valeur AICc la plus faible est le meilleur (autrement dit, en prenant en considération la complexité du modèle, le modèle avec la valeur AICc la plus faible est le mieux adapté aux données observées).
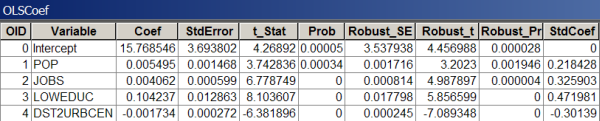
La création des tables des diagnostics et des coefficients pour vos modèles des moindres carrés ordinaires finaux capture des éléments importants du rapport des moindres carrés ordinaires. La table des coefficients comprend la liste des variables explicatives utilisées dans le modèle avec leurs coefficients, leurs coefficients normalisés, leurs erreurs standard, ainsi que leurs probabilités. Le coefficient est une estimation de la variation de la variable dépendante si un changement d’une unité se produit dans la variable explicative associée. Les unités des coefficients correspondent aux variables explicatives. Si, par exemple, vous avez une variable explicative pour la population totale, les unités du coefficient de cette variable reflètent les gens. Si une autre variable explicative correspond à la distance (mètres) par rapport à la gare ferroviaire, les unités du coefficient reflètent les mètres. Lorsque les coefficients sont convertis en écarts types, ce sont des coefficients normalisés. Vous pouvez utiliser les coefficients normalisés pour comparer l'effet que différentes variables explicatives ont sur la variable dépendante. La variable explicative dont le coefficient normalisé est le plus élevé après la suppression du symbole +/- (prenez la valeur absolue) a l’effet le plus important sur la variable dépendante. Les interprétations des coefficients ne peuvent toutefois avoir lieu qu'à la lumière de l'erreur standard. Les erreurs standard indiquent la probabilité d'obtention des mêmes coefficients si vous pouviez rééchantillonner vos données et recalibrer votre modèle un nombre infini de fois. Des erreurs standard importantes pour un coefficient signifient que le processus de rééchantillonnage résulterait en une vaste plage de valeurs de coefficients possibles. Des erreurs standard moindres indiquent que le coefficient serait assez homogène.
La table des diagnostics comprend les résultats de chaque test de diagnostic, ainsi que des conseils sur l'interprétation de ces résultats.

Ressources supplémentaires
La page Spatial Statistics Resources contient des ressources qui vous permettront d’approfondir vos connaissances sur la régression des moindres carrés ordinaires. Commencez par lire la rubrique Principes de base de l’analyse de régression ou exercez-vous avec le didacticiel Regression Analysis. Appliquez l’analyse de régression à vos propres données, en vous reportant à la table des problèmes courants et à la rubrique Ce que l’on ne vous dit pas sur l’analyse de régression pour obtenir des stratégies supplémentaires. Si vous avez des difficultés à trouver un modèle correctement spécifié, l’outil Régression exploratoire peut se révéler utile.
Les ressources suivantes sont également utiles :
- Mitchell, Andy. The ESRI Guide to GIS Analysis, Volume 2. ESRI Press, 2005.
- Wooldridge, J. M. Introductory Econometrics: A Modern Approach. South-Western, Mason, Ohio, 2003.
- Hamilton, Lawrence C. Regression with Graphics. Brooks/Cole, 1992.
Vous avez un commentaire à formuler concernant cette rubrique ?