Disponible avec une licence Geostatistical Analyst.
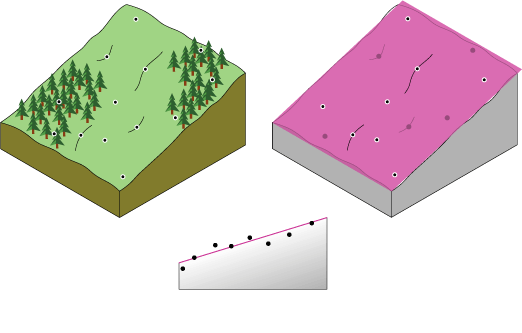
La rubrique Analyse des propriétés de la surface des localisations à proximité a présenté l’interpolation qui dépend de la distance. Il existe d’autres solutions pour prévoir les valeurs des localisations non mesurées. Un autre site proposé pour la zone d’observation se situe sur la face d’une colline légèrement inclinée. La face de la colline est un plan incliné. Cependant, les localisations des échantillons se situent dans des légères dépressions ou sur de petites buttes (variation locale). L’utilisation de voisins locaux pour prévoir une localisation risque de surestimer ou de sous-estimer la prévision en raison de l’influence des dépressions et des buttes. De plus, il peut arriver que vous captiez la variation locale et que vous ne capturiez pas le plan incliné dans son ensemble (appelé tendance). La possibilité d’identifier et de modéliser les structures locales et les tendances de surface peut augmenter la précision de la surface prévue.
Interpolation polynomiale globale
Pour faire reposer la prévision sur la tendance de remplacement, vous pouvez ajuster un plan entre les points d’échantillonnage. Un plan est un cas particulier d’une famille de formules mathématiques appelées polynômes. Vous pouvez ensuite déterminer la hauteur inconnue à partir de la valeur du plan de la localisation de la prévision. Le plan peut se situer au-dessus de certains points et sous d’autres points. L’objectif de l’interpolation consiste à minimiser l’erreur. Vous pouvez mesurer l’erreur en soustrayant chaque point mesuré de sa valeur prévue sur le plan, la mettre au carré et ajouter ces erreurs au carré. Cette somme est appelée ajustement par les moindres carrés. Ce processus constitue la base théorique de l’interpolation polynomiale globale de premier ordre.
Mais que se passe-t-il si vous essayez d’ajuster le plan sur un paysage en forme de vallée ? Il est difficile d’obtenir une bonne surface à partir d’un plan. Cependant, si vous le courbez une fois, vous pouvez peut-être obtenir un meilleur ajustement (à savoir vous rapprocher de plus de valeurs). L’application d’une courbure est la base de l’interpolation polynomiale globale de second ordre (voir ci-dessous). Deux courbures dans le plan entraîneraient un polynôme de troisième ordre, et ainsi de site. Les courbures peuvent se produire dans les deux directions, ce qui permet d’obtenir une surface en forme de bol.

En savoir plus sur le fonctionnement de l’interpolation polynomiale globale
Rubriques connexes
Vous avez un commentaire à formuler concernant cette rubrique ?