De nombreux outils et méthodes de la boîte à outils Statistiques spatiales nécessitent de définir des relations spatiales entre les entités. Cela inclut l’identification des entités considérées comme voisines les unes des autres et de l’influence que les entités voisines ont les unes sur les autres. Cette structure, définie par l’association d’un type de voisinage et d’une structure de pondération, constitue la base de nombreuses analyses spatiales.
Relations spatiales
Une différence importante entre statistiques spatiales et classiques est que les premières intègrent les relations spatiales directement dans leurs formules mathématiques et leurs modèles. Par conséquent, de nombreux outils incluent un paramètre Conceptualisation des relations spatiales, Type de voisinage ou Contrainte spatiale qui vous permet de définir les relations spatiales entre les entités.
Différentes relations spatiales mettent en avant différents aspects de la structure spatiale. Par exemple, dans une étude du marché de l’immobilier, il peut être pertinent de définir le voisinage de chaque logement comme les quelques propriétés les plus proches, pondérées par distance, en supposant que les ventes à proximité sont celles qui ont le plus d’influence. D’autres situations peuvent nécessiter des définitions plus larges ou plus complexes, comme la création de relations entre des villes en fonction du nombre de voyageurs entre elles (lorsque des villes géographiquement éloignées sont malgré tout hautement dépendantes sur le plan économique). Ces choix affectent de nombreux facteurs, allant de la détection des modèles spatiaux au comportement de ces derniers. Il est donc important de réfléchir aux relations spatiales qui sont les plus adaptées à vos données et vos questions.
Lors de l’exécution d’une analyse statistique spatiale telle que l’analyse des points chauds ou l’analyse des valeurs aberrantes et des agrégats, vous pouvez définir les relations spatiales directement dans les outils à l’aide de leurs paramètres. Toutefois, vous pouvez également créer un fichier de matrice de pondérations spatiales (.swm) pour stocker les voisins et les pondérations afin de les réutiliser dans divers outils.
Différents outils et méthodes présentent diverses options pour définir les relations spatiales. Bien qu’aucun outil ne prenne en charge toutes les relations possibles, l’outil Générer la matrice de pondérations spatiales offre la plus grande palette de relations spatiales et le fichier en sortie peut être utilisé et réutilisé dans d’autres outils d’analyse. Pour toutes les relations spatiales à l’exception des plus simples, il est recommandé de commencer par définir les relations spatiales dans un fichier de matrice de pondérations spatiales, puis d’utiliser le fichier dans des outils d’analyse spatiale.
Les différentes relations spatiales prises en charge par les outils sont décrites dans les sections suivantes :
Inverse de la distance
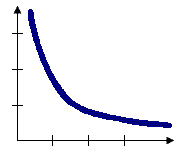
La relation spatiale d’inverse de la distance est une relation d’impédance ou de fréquentation en fonction de la distance, dans laquelle la pondération des entités voisines diminue en divisant la distance entre l’entité voisine et l’entité focale. Toutes les entités ont un impact ou une influence sur les autres entités, mais plus elles sont éloignées, plus cet impact est réduit. Cet inverse de la distance est également souvent utilisé avec une puissance, par exemple l’inverse de la distance au carré, ce qui provoque une diminution encore plus rapide de la pondération. Il est généralement recommandé d’utiliser une distance seuil avec les relations d’inverse de la distance afin de réduire le nombre de voisins dont la pondération est très proche de 0. Lorsqu’une distance seuil est spécifiée, une valeur de seuil par défaut est calculée pour vous, mais vous pouvez forcer toutes les entités à être voisines de toutes les autres entités en définissant la distance seuil sur 0.
Canal de distance constante

La relation spatiale de canal de distance constante impose une sphère d’influence autour de chaque entité, et toutes les entités dans une distance seuil donnée autour de l’entité focale sont incluses comme voisines. Cette option est appropriée si vous souhaitez évaluer les propriétés statistiques de vos données à une échelle spatiale (fixe) donnée. Si vous étudiez la migration quotidienne de travailleurs et que vous savez que le trajet moyen jusqu’au lieu de travail est de 15 km, par exemple, une distance de 15 km convient pour votre analyse. Pour connaître les stratégies qui permettent d’identifier une échelle d’analyse appropriée, reportez-vous à la rubrique Bonnes pratiques pour la sélection d’une valeur de bande de distance fixe.
Zone d'indifférence

La relation spatiale de zone d’indifférence combine les relations spatiale de canal de distance constante et d’inverse de la distance. Les entités situées dans la distance seuil sont comprises dans les analyses de l’entité cible. Une fois la distance seuil dépassée, le niveau d’influence (la pondération) chute rapidement. Cette méthode est appropriée si vous voulez conserver l’échelle d’analyse fixe, mais que vous ne souhaitez pas imposer des limites strictes sur les entités voisines incluses dans les calculs d’entités cible.
Contiguïté de polygones
Pour les classes d’entités surfaciques, vous pouvez choisir de définir des voisins en utilisant tous les polygones contigus au polygone focal. Vous pouvez également choisir d’inclure les polygones en tant que voisins s’ils partagent uniquement un angle (contiguïté Reine) ou d’inclure uniquement les voisins qui partagent une arête (contiguïté Tour). Dans divers outils, ces options sont appelées respectivement Angles des segments de contiguïté et Arêtes de contiguïté uniquement. Si deux polygones se chevauchent en partie, ils sont considérés comme étant voisins par les deux options de contiguïté.
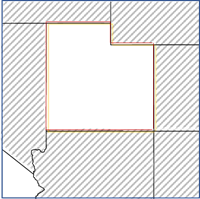
La contiguïté de polygones peut également être étendue à des ordres supérieurs, dans lesquels l’ordre est le nombre d’étapes qui seraient nécessaires pour passer du polygone focal à ses voisins. La contiguïté de premier ordre signifie que seuls les voisins immédiats du polygone focal sont considérés comme voisins (ceux qui peuvent être atteints en une seule étape). L’ordre deux signifie que tous les polygones pouvant être atteints en deux étapes ou moins (les voisins de premier ordre et tous leurs voisins de premier ordre) sont inclus comme voisins. Si les polygones sont organisés dans une grille, les ordres supérieurs forment des anneaux concentriques autour du polygone focal. Il est généralement recommandé d’éviter d’utiliser des ordres de polygones supérieurs à 3. Vous pouvez créer des relations spatiales de contiguïté d’ordre supérieur à l’aide de l’outil Générer la matrice de pondérations spatiales.
K voisins les plus proches
La relation spatiale des K voisins les plus proches utilise un nombre défini de K entités les plus proches en tant que voisins, la valeur K étant fournie par le paramètre Nombre de voisins. Sur les sites à densité d’entités élevée, l’échelle spatiale de l’analyse est réduite. De la même façon, sur les sites à densité d’entités faible, l’échelle spatiale de l’analyse sera plus importante. Un avantage de ce modèle de relations spatiales est qu'il garantit l'existence de voisins pour chaque entité cible, même si les densités cible présentent de fortes variations dans la zone d'étude.

triangulation de Delaunay
La relation spatiale de triangulation de Delaunay construit des voisins en créant des triangles de Voronoi à partir d’entités ponctuelles ou de centroïdes d’entités de sorte que chaque point ou centroïde soit un nœud de triangle. Les nœuds connectés par le bord d'un triangle sont considérés comme voisins. L’utilisation de la triangulation de Delaunay garantit que chaque entité possède au moins un voisin, même si les données incluent des îles ou des densités d’entités très variables. N'utilisez pas la triangulation de Delaunay si certaines entités coïncident.

Fenêtre spatio-temporelle
Cette option permet de définir des relations entre entités en termes de fenêtres d’espace (distance constante) et de temps (intervalle temporel constant). Cette option est disponible lorsque vous créez un fichier de matrice de pondérations spatiales à l’aide de l’outil Générer la matrice de pondérations spatiales. Lorsque vous sélectionnez l’option Fenêtre spatio-temporelle, vous devez spécifier une valeur pour les paramètres suivants : Champ de date/heure, Type d’intervalle de date/heure (heures, jours ou mois, par exemple) et Valeur d’intervalle de date/heure. La valeur d'intervalle est un entier. Si, par exemple, vous avez sélectionné le type d’intervalle Heures et 3 comme valeur d’intervalle, deux entités seront considérées comme voisines si les valeurs de leur champ de date/heure ont moins de trois heures d’écart. Avec cette conceptualisation, les entités sont voisines si elles se trouvent dans la limite de distance spécifiée et si elles sont comprises dans l’intervalle de temps spécifié de l’entité cible. Par exemple, vous pouvez sélectionner l’option Fenêtre spatio-temporelle pour le paramètre Conceptualisation des relations spatiales si vous voulez créer un fichier de matrice de pondérations spatiales à utiliser avec l’outil Analyse de points chauds, pour identifier les points chauds spatio-temporels. Pour obtenir des informations supplémentaires, dont la procédure à suivre pour visualiser les résultats, consultez la rubrique Analyse spatio-temporelle. D'autres méthodes sont disponibles pour vous aider à visualiser en 3D un cube spatio-temporel netCDF.
Extraire les pondérations spatiales à partir du fichier
Si vos relations spatiales sont définies dans un fichier de matrice de pondérations spatiales (.swm), utilisez cette option pour fournir le fichier et appliquer les pondérations personnalisées à l’analyse. Vous pouvez créer ces fichiers à l’aide des outils Générer la matrice de pondérations spatiales, Générer les pondérations spatiales de réseau, Explorateur de voisinage ou d’autres outils du jeu d’outils Utilitaires des composants spatiaux (vecteurs propres de Moran).
Pratiques conseillées pour la sélection de relations spatiales
Plus la modélisation des interactions entre les entités dans l’espace est réaliste, plus les résultats sont précis. Le choix des relations spatiales doit refléter les relations inhérentes entre les entités que vous analysez. Votre choix peut également être motivé par les caractéristiques de vos données.
Les méthodes d’inverse de la distance, par exemple, sont mieux adaptées aux données continues ou à des processus de modèle dans lesquels, plus deux entités sont proches dans l’espace, plus elles sont susceptibles d’interagir ou de s’influencer mutuellement. Grâce à cette relation spatiale, chaque entité est potentiellement voisine de toutes les autres, et, dans le cas de jeux de données importants, le nombre de calculs impliqués est énorme. Essayez toujours d’inclure une distance seuil lorsque vous utilisez les relations d’inverse de la distance. Ce point est particulièrement important pour les jeux de données volumineux. Si vous n’indiquez pas de distance seuil, cette valeur est calculée pour vous, mais il ne s’agit pas nécessairement de la distance la plus appropriée pour votre analyse. La distance seuil par défaut est la distance minimale qui garantit que chaque entité possède au moins un voisin.
L’option Canal de distance constante fonctionne bien pour des données ponctuelles et constitue souvent un choix raisonnable pour les données surfaciques lorsque la taille des polygones est très variable (polygones très grands à la limite de la zone d’étude et polygones très petits en son centre, par exemple) et que vous voulez garantir une échelle d’analyse constante. Pour connaître les stratégies qui permettent de déterminer une valeur de bande de distance appropriée pour l’analyse, reportez-vous à la rubrique Bonnes pratiques pour la sélection d’une valeur de bande de distance fixe.
L’option Zone d’indifférence fonctionne bien quand la distance constante est adéquate, mais l’imposition de limites strictes sur les relations de voisinage ne constitue pas une représentation précise de vos données. La relation de zone d’indifférence considère toute entité comme un voisin de toutes les autres entités.
Les relations de contiguïté des polygones (options Arêtes de contiguïté uniquement et Angles des arêtes de contiguïté) sont efficaces si les polygones sont de taille et de distribution similaires et que les relations spatiales sont une fonction de la proximité des polygones (si deux polygones partagent une limite, leur interaction spatiale augmente). Lorsque vous sélectionnerez une conceptualisation de contiguïté de polygone, vous souhaiterez presque toujours sélectionner la standardisation par lignes pour les outils possédant le paramètre Standardisation par lignes.
L’option K nearest neighbors (K voisins les plus proches) est efficace lorsque vous souhaitez garantir un nombre minimal de voisins dans l’analyse. Surtout si les valeurs associées aux entités sont faussées (qu’elles ne sont pas distribuées normalement), il est important que chaque entité soit évaluée dans le contexte d’au moins huit voisins (il s’agit là uniquement d’une règle générale). Si la distribution de vos données varie dans votre zone d'étude et que certaines entités sont éloignées de toutes les autres entités, cette méthode fonctionne bien. Notez toutefois que le contexte spatial de votre analyse change selon les variations rencontrées dans la rareté ou la densité de vos entités. Lorsque la détermination de l'échelle d'analyse est moins importante que la détermination du nombre de voisins, la méthode des K voisins les plus proches est adaptée.
L’option Triangulation de Delaunay (parfois appelée voisins naturels) convient lorsque vos données comprennent des polygones d’îles (des polygones isolés ne partageant aucun bord avec d’autres polygones) ou si la distribution spatiale d’entités est très inégale.
Les paramètres de l’option Space time window (Fenêtre spatio-temporelle) permettent de définir des relations entre entités en termes de proximité spatiale et de proximité temporelle. Cette option convient, par exemple, pour identifier les points chauds spatio-temporels ou créer des groupes dans lesquels l’appartenance est contrainte par la proximité spatiale et temporelle. Vous trouverez des exemples d'analyse spatio-temporelle, ainsi que des stratégies de représentation efficace des résultats de ce type d'analyse, dans la rubrique Analyse spatio-temporelle.
Pour certaines applications, l'interaction spatiale est mieux modélisée en termes de temps de trajet ou distance à parcourir. Si vous modélisez l’accessibilité de services urbains, par exemple, ou si vous cherchez des points chauds de criminalité urbaine, la modélisation de relations spatiales en termes de réseau est recommandée. Utilisez l’outil Générer les pondérations spatiales de réseau.
Si aucune des options prédéfinies n’est adaptée à votre analyse, vous pouvez créer un fichier texte ASCII ou une table incluant les relations d’entité à entité de votre choix puis les utiliser pour créer un fichier de matrice de pondérations spatiales. Si une des options ci-dessus est proche de la relation spatiale que vous souhaitez, vous pouvez utiliser l’outil Générer la matrice de pondérations spatiales pour créer un fichier de matrice de pondérations spatiales de base, puis modifier votre fichier de matrice de pondérations spatiales.
Structures de pondération
Tandis que les relations spatiales d’inverse de la distance et de zone d’indifférence appliquent des pondérations à tous les voisins en fonction de la distance, plusieurs outils vous permettent de spécifier une relation spatiale en définissant en premier lieu une structure de voisinage (telle qu’un canal de distance ou les K voisins les plus proches), puis en spécifiant une méthode pour appliquer des pondérations aux voisins. À l’instar de la pondération par inverse de la distance, il est courant d’attribuer une pondération plus élevée aux voisins proches de l’entité focale à l’aide d’une fonction, appelée un noyau, qui diminue avec la distance. La pondération par noyau présente l’avantage de fournir des pondérations stables aux voisins, qu’ils soient proches ou lointains, alors que la pondération par inverse de la distance rencontre des problèmes avec des distances inférieures à un, et les pondérations diminuent rapidement en s’éloignant de l’entité focale. Tous les noyaux doivent utiliser une bande passante qui peut être constante ou adaptative, et qui définit la rapidité selon laquelle les pondérations diminuent en fonction de la distance. Les noyaux courants incluent les noyaux bicarrés, gaussiens, triangulaires et quadratiques. Pour en savoir plus sur la pondération par noyau, consultez la rubrique Fonctionnement des résumés statistiques de voisinage.
L’outil Générer la matrice de pondérations spatiales vous permet en outre d’effectuer une pondération selon la longueur de la bordure lorsque vous définissez les relations spatiales à l’aide de la contiguïté des polygones. Cela vous permet d’attribuer davantage d’influence aux entités qui partagent une plus grande partie de la bordure des entités focales. Vous pouvez également effectuer la pondération selon les valeurs d’un champ, comme la population ou la zone surfacique, afin d’attribuer des pondérations plus élevées aux entités ayant des valeurs de champs supérieures. En cas de pondération par bordure partagée ou par valeurs de champs, toutes les pondérations sont standardisées par lignes.
Méthode de distance
Plusieurs outils vous donnent le choix entre distance euclidienne ou de Manhattan.
- La distance euclidienne est calculée de la manière suivante
D = sq root [(x1–x2)**2.0 + (y1–y2)**2.0]où (x1,y1) est la coordonnée du point A, (x2,y2) la coordonnée du point B et D la distance en ligne droite entre les points A et B.
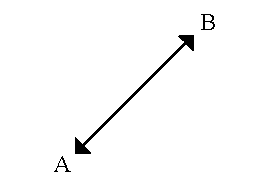
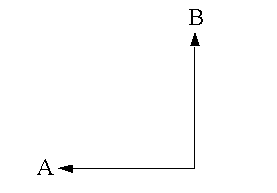
- La distance de Manhattan est calculée de la manière suivante
D = abs(x1–x2) + abs(y1–y2)où (x1,y1) est la coordonnée du point A, (x2,y2) est la coordonnée du point B et D est la différence verticale plus horizontale entre les points A et B. Il s’agit de la distance que vous devez parcourir si vous êtes limité aux déplacements nord-sud et est-ouest. Cette méthode est généralement plus appropriée que la distance euclidienne lorsque le trajet est limité à un réseau de rues et si les coûts de déplacement dans le réseau de rues ne sont pas disponibles.
Lorsque vos entités en entrée ne sont pas projetées (c’est-à-dire, lorsque les coordonnées sont exprimées en coordonnées de latitude et de longitude) ou que le système de coordonnées en sortie est un système de coordonnées géographiques, les distances sont calculées à l’aide des mesures à la corde et le paramètre Méthode de calcul de la distance est désactivé. Les mesures de distance de corde sont utilisées, car elles sont rapides à calculer et produisent des évaluations précises des distances géodésiques réelles, du moins pour les points se trouvant à environ 30 degrés les uns des autres. Les distances de corde sont basées sur un modèle terrestre sphérique. La distance de corde entre deux points à la surface correspond à la distance en ligne droite en 3D entre eux (cette ligne droite traverse la Terre). Les distances à la corde sont exprimées en mètres.
Attention :
Il est recommandé de projeter vos données si votre zone d’étude s’étend au-delà de 30 degrés. Les distances à la corde ne constituent pas une estimation fiable des distances géodésiques au-delà de 30 degrés.
Auto-pondération
Plusieurs outils permettent de définir des entités et des pondérations comme voisines d’elles-mêmes. Cela s’appelle l’auto-pondération. Par exemple, vous pouvez utiliser des auto-pondérations afin de refléter les coûts de déplacement intra-zonaux d’après la taille du polygone. L’outil Analyse des points chauds permet d’indiquer un champ représentant les auto-pondérations dans le paramètre Champ de potentiel propre. Les outils Générer les pondérations spatiales de réseau et Résumés statistiques de voisinage vous permettent d’inclure des auto-pondérations à l’aide du paramètre Inclure l’entité focale. Plusieurs autres outils, comme Association spatiale bivariée (statistique L de Lee), ajoutent automatiquement des auto-pondérations à toute relation spatiale fournie.
Standardisation par lignes
La standardisation par lignes est recommandée chaque fois que la répartition de vos entités est potentiellement influencée par la conception de l'échantillonnage ou un plan d'agrégation imposé. Lorsque la standardisation par lignes est sélectionnée, chaque pondération est divisée par la somme des lignes (la somme des pondérations de toutes les entités voisines) afin d’obtenir une somme de 1. La pondération standardisée de lignes est souvent utilisée avec des voisinages de distance constante et presque toujours utilisée pour les voisinages d’après la contiguïté des polygones. Cela permet de réduire le biais occasionné par les entités possédant des nombres de voisins différents. La standardisation par lignes crée une structure de pondération relative, plutôt qu’absolue, qui convient par exemple lors de l’utilisation de limites administratives.
Canal de distance
Le paramètre Canal de distance (parfois appelé distance seuil) définit l’échelle d’analyse de la plupart des relations spatiales pour diverses relations spatiales. Il est important de choisir une distance appropriée. Certaines statistiques spatiales nécessitent que chaque entité ait au moins un voisin pour que l'analyse soit fiable. Si le canal de distance est trop petit (et que certaines entités n’ont pas de voisins), un message d’avertissement s’affiche. L'outil Calculer la bande de distance à partir du nombre de voisins évalue les distances minimale, maximale et moyenne pour un nombre spécifié de voisins et peut vous aider à déterminer une valeur de canal distance adéquate à utiliser pour l'analyse. Pour plus d’indications, consultez la rubrique Bonnes pratiques pour la sélection d’une valeur de bande de distance fixe.
Si aucune valeur n'est spécifiée, une distance seuil par défaut est calculée. La table suivante indique comment les différentes relations spatiales se comportent pour chacun des trois types en entrée possibles (les valeurs négatives ne sont pas valides) :
| Inverse de la distance, Inverse de la distance au carré | Canal distance constante, Zone d'indifférence | Contiguïté polygonale, Triangulation de Delaunay, K voisins les plus proches | |
|---|---|---|---|
| 0 | Aucun seuil ni limite n'est appliqué, toutes les entités sont des voisins de toutes les autres entités. | Non valide. Une erreur d’exécution est générée. | Ignoré |
| vide | Une distance par défaut est calculée. Cette valeur est la distance minimale qui permet de s'assurer que chaque entité possède au moins un voisin. | Une distance par défaut est calculée. Cette valeur est la distance minimale qui permet de s'assurer que chaque entité possède au moins un voisin. | Ignoré |
| nombre positif | La valeur positive, non zéro, spécifiée est utilisée comme distance limite, les relations de voisinage existent uniquement parmi les entités au sein de cette distance les unes par rapport aux autres. | Dans le cas du canal de distance constante, seules les entités qui se trouvent dans cette limite spécifiée les unes par rapport aux autres sont voisines. Dans le cas de la zone d’indifférence, les entités au sein de cette limite spécifiée les unes par rapport aux autres sont voisines, ainsi que celles situées en-dehors de la limite, mais celles-ci ont une pondération ou une influence qui diminue à mesure que la distance augmente. | Ignoré |
Nombre de voisins
Le paramètre Nombre de voisins sert d’objectif pour diverses relations spatiales. Pour les K voisins les plus proches, chaque entité cible utilise les K entités les plus proches (où K est le nombre de voisins spécifié). Pour l’inverse de la distance et le canal de distance, la distance seuil s’étend pour l’entité afin de s’assurer qu’elle a au moins K entités. Pour les relations spatiales de contiguïté des polygones, des voisins supplémentaires sont ajoutés en fonction de la proximité des centroïdes des entités afin de s’assurer qu’il existe au moins K voisins.
Fichier texte de matrice de pondérations
Plusieurs outils permettent de définir des relations spatiales entre entités en fournissant un fichier de matrice de pondérations spatiales (.swm). Les pondérations spatiales sont des nombres entre 0 et 1 qui reflètent l’interaction et l’influence entre toutes les entités dans le jeu de données. Vous pouvez créer le fichier de matrice de pondérations spatiales à l’aide de l’outil Générer la matrice de pondérations spatiales ou il peut s’agir d’un simple fichier ASCII.
Lorsque le fichier de matrice de pondérations spatiales est un simple fichier de texte ASCII, la première ligne doit être le nom d'un champ d'ID unique. Cela vous permet d'utiliser tout champ numérique dans votre jeu de données comme ID lors de la génération de ce fichier. Cependant, ce champ doit être de type entier (long ou court) et contenir des valeurs uniques pour chaque entité. Après la première ligne, le fichier de pondérations spatiales doit contenir les trois colonnes suivantes :
- ID d'entité de départ
- ID d'entité d'arrivée
- Pondération
Supposons, par exemple, que vous ayez trois stations service. Le champ que vous utilisez comme champ d’ID est appelé StationID, et les ID d’entités sont 1, 2 et 3. Vous souhaitez modéliser les relations spatiales entre ces trois stations service grâce à l’inverse du temps de trajet. Le fichier ASCII doit ressembler à ce qui suit :

Saisir les valeurs du fichier de matrice de pondérations spatiales peut être fastidieux. Une approche plus efficace consiste à utiliser l’outil Générer la matrice de pondérations spatiales pour créer un fichier de matrice de pondérations spatiales.
Fichier de matrice de pondérations spatiales (.swm)
L’outil Générer la matrice de pondérations spatiales crée un fichier de matrice de pondérations spatiales (.swm) qui définit les relations spatiales entre toutes les entités de votre jeu de données en fonction des paramètres que vous spécifiez. Ce fichier est créé en format binaire afin que les valeurs qu'il contient ne puissent pas être vues directement. Pour consulter ou modifier les relations entre entités dans un fichier .swm, utilisez l’outil Convertir la matrice de pondérations spatiales en table.
Vous pouvez également utiliser l’outil Générer la matrice de pondérations spatiales pour convertir cette table en fichier .swm. La table doit contenir les champs suivants :
| Nom du champ | Description |
|---|---|
| <Nom du champ d’ID unique> | Champ de nombre entier avec un ID unique pour chaque entité. Le nom et le type du champ doivent correspondre au champ d’ID unique associé des entités. Par exemple, si une entité avec l’ID 6 a quatre voisins, la valeur 6 est répétée quatre fois dans ce champ : une fois pour chaque voisin. |
| NID | Champ d’entier contenant l’ID du voisin. |
| WEIGHT | Pondération numérique entre 0 et 1 représentant l’influence, ou l’interaction, entre les deux entités. |
La méthode la plus simple pour mettre à jour un fichier .swm avec des pondérations personnalisées consiste à créer un fichier .swm inital et de le convertir en table. Cette table contient les bons noms de champs et propriétés, pour que vous puissiez créer et mettre à jour les lignes afin d’attribuer des relations et pondérations personnalisées entre voisins. La table doit également être triée par ID unique, puis par ID de voisin.
Partage de fichiers de matrice de pondérations spatiales
La sortie de l’outil Générer la matrice de pondérations spatiales est un fichier .swm. Ce fichier est lié à la classe d’entités en entrée, au champ d’ID unique et aux paramètres du système de coordonnées en sortie lors de la création du fichier .swm. D’autres personnes peuvent dupliquer les relations spatiales que vous définissez pour l’analyse à l’aide de votre fichier .swm et de la même classe d’entités en entrée ou d’une classe d’entités liant toutes les entités (ou un sous-ensemble de celles-ci) à un champ Unique ID correspondant. Évitez d’utiliser un système de coordonnées en sortie différent de la référence spatiale des entités d’origine, particulièrement si vous projetez de partager vos fichiers .swm avec d’autres personnes. Nous vous recommandons de commencer par projeter les entités en entrée en premier, puis de créer le fichier de matrice de pondérations spatiales pour la nouvelle référence spatiale.
Pondérations spatiales de réseau
Dans certaines analyses, les relations spatiales sont mieux définies par distance à parcourir le long d’un réseau que par proximité en ligne droite. Par exemple, lorsque vous modélisez les temps de réponse des services d’urgence, il peut être plus approprié de définir des voisins en fonction du temps de trajet le plus court via un réseau routier que par distance euclidienne. Pour les jeux de données comme celui-ci, vous pouvez utiliser l’outil Générer les pondérations spatiales de réseau pour définir des relations spatiales à partir d’un jeu de données réseau qui définit des relations spatiales en termes de structure de réseau sous-jacente.
Rubriques connexes
Vous avez un commentaire à formuler concernant cette rubrique ?