L’outil Réduction des dimensions permet de réduire le nombre de dimensions d’un ensemble de variables continues en agrégeant le plus grand nombre possible de variances dans le moins de composantes possibles à l’aide d’Analyse des Composantes Principales (ACP) ou d’Analyse de discriminant linéaire par rang réduit (LDA). Les variables sont spécifiées sous forme de champs dans une couche d’entités ou table en entrée, et de nouveaux champs représentant les nouvelles variables sont enregistrés dans la classe d’entités ou table en sortie. Le nombre de nouveaux champs sera moindre que le nombre de variables d’origine tout en maintenant le volume le plus élevé possible de variance par rapport aux variables d’origine.
La réduction des dimensions est généralement utilisée pour explorer les relations multivariées entre des variables et pour réduire le coût de calcul des algorithmes d’apprentissage automatique où la mémoire requise et le temps de traitement dépendent du nombre de dimensions dans les données. Utiliser les composantes à la place des données d’origine ou des algorithmes d’apprentissage automatiques permet souvent d’obtenir des résultats comparables (ou même meilleurs) tout en consommant moins de ressources de calcul.
Il est recommandé d’utiliser la PCA lorsque vous tentez de procéder à une analyse ou d’utiliser une méthode d’apprentissage machine dans laquelle les composantes sont utilisées pour prévoir la valeur d’une variable continue. De plus, la LDA requiert de classer chaque enregistrement dans une catégorie (celle de l’utilisation du sol, par exemple). Il est recommandé de choisir la LDA pour utiliser une méthode d’analyse ou de Machine Learning selon laquelle les composantes sont utilisées pour classer la catégorie de variables catégorielles en fonction des champs d’analyse numérique.
Applications possibles
Il est possible d’utiliser cet outil dans les types de scénarios suivants :
- Vous disposez d’une classe d’entités contenant de nombreux champs qui sont difficiles à visualiser en même temps. En réduisant le jeu de données à deux dimensions, vous pouvez visualiser les données dans un diagramme pour voir les interactions multivariées entre les champs en deux dimensions.
- Vous pouvez utiliser les outils d’analyse du jeu d’outils Modélisation de relations spatiales, tels que Régression linéaire généralisée ou Régression pondérée géographiquement (GWR), mais de nombreux champs sont étroitement corrélés les uns aux autres. En réduisant le nombre de dimensions des variables explicatives, les outils d’analyse peuvent être plus stables et moins enclins au surajustement des données d’apprentissage.
- Vous utilisez une méthode d’apprentissage machine dont la durée d’exécution augmente rapidement avec le nombre de variables en entrée. En réduisant le nombre de dimensions, vous pouvez obtenir des résultats d’analyse comparables en utilisant moins de mémoire et dans un délai plus court.
Fonctionnement de PCA
LA PCA fonctionne à l’aide de composantes de construction en séquence qui capturent un certain pourcentage de la variance totale de tous les champs d’analyse. Chaque composante en elle-même est une combinaison linéaire (somme pondérée) de chacun des champs d’analyse, les pondérations étant appelées chargements de la composante. Avec les champs d’analyse, les chargements forment un vecteur propre, indiquant la contribution de chaque champ d’analyse à la composante. La composante est également associée à un vecteur propre, qui représente la variance totale maintenue par la composante.
Pour deux champs d’analyse, vous pouvez visualiser la PCA (ou ACP) géométriquement sous la forme d’axes de rotation dans l’espace de données dans lequel la rotation optimise le rapport de variabilité des nouveaux axes, comme illustré par l’image suivante :
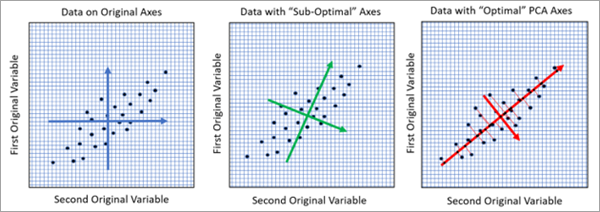
Dans l’image de gauche, chaque point est un enregistrement de la table en entrée tracée en deux dimensions avec les valeurs des deux champs d’analyse sur l’axe x et l’axe y. La longueur des axes bleus représente la variance de chacune des deux variables. Le deux flèches bleues sont de longueurs à peu près égales, indiquant que les deux variables présentent des variances à peu près équivalentes. Dans l’image du milieu, les axes ont été pivotés pour mieux représenter la relation linéaire entre les variables. L’un des axes verts est légèrement plus long que l’autre, indiquant une variance plus importante dans cette direction. Toutefois, cette rotation n’est pas optimale. L’image de droite présente la rotation optimale déterminée par la PCA alignée sur la relation linéaire entre les variables. Cette rotation génère un axe rouge avec le plus grand nombre de variances. L’axe rouge le plus grand correspond à la première composante principale et constitue la meilleure représentation à une dimension de données à deux dimensions. Dans les trois images, la variance totale des variables d’origine est la même, mais l’image de droite a attribué la plus grande quantité possible de variances à la première composante, laissant la plus petite quantité possible de variances à la deuxième composante.
Vous pouvez voir les valeurs propres et les vecteurs propres de chaque composante en utilisant les paramètres Output Eigenvalues Table (Tableau de valeurs propres en sortie) et Output Eigenvectors Table (Tableau de vecteurs propres en sortie), le tableau des vecteurs propres étant accompagné d’un diagramme à barres qui affiche les chargements de chaque composante. Pour la totalité des détails mathématiques de la PCA, consultez la section Ressources supplémentaires.
Fonctionnement de l’analyse de discriminant linéaire par rang réduit
LDA (souvent abrégée en RR-LDA ou Reduced-Rank LDA) fonctionne à l’aide de composantes de construction en séquence qui optimisent la séparation entre classes d’une variable catégorielle. La méthode cherche à réduire les dimensions des champs d’analyse continue tout en conservant la plus grande précision dans le classement de la catégorie de variables catégorielles. Comme pour une PCA, les composantes de la LDA sont également associées à des vecteurs propres et des valeurs propres afin de représenter la contribution des champs d’analyse à chaque composante et la quantité de variances maintenue par chaque composante.
Pour deux variables d’analyse continue et une variable catégorielle avec deux catégories, la LDA présente également une interprétation géométrique 2D impliquant des rotations. L’image ci-dessous présente un jeu de données dans lequel chaque point représente un enregistrement du jeu de données en entrée. L’axe x et l’axe y sont les deux champs d’analyse continue, et les points sont de couleur rouge ou bleue en fonction de leur catégorie. Les distributions rouges ou bleues sont celles des catégories projetées sur l’axe y. Il existe une certaine divisibilité dans les distributions des classes, mais leur superposition est importante et sont difficiles à séparer. Un manque similaire de séparation se produit en projetant sur l’axe x.
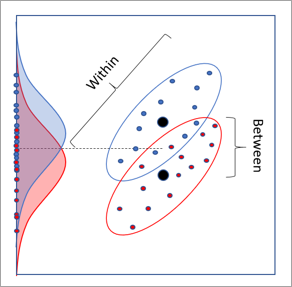
L’image ci-dessous présente la rotation optimale de l’axe déterminée par la LDA. Cette rotation entraîne la plus grande séparation entre les distributions des catégories, ce qui permet d’obtenir le taux le plus élevé de classification de la catégorie.
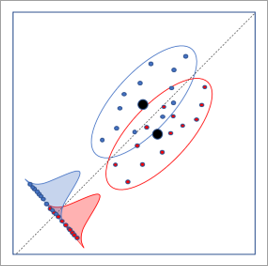
Si au moins deux composantes sont créées, les entités en sortie comportent un nuage de points Discriminant linéaire. Les valeurs des première et deuxième composantes sont tracées sur les axes, et les points sont colorés par catégorie. Si les deux premières composantes conservent des informations suffisantes pour distinguer les catégories, les points du nuage peuvent s’agréger par catégorie.

Vous pouvez afficher les valeurs propres et les vecteurs propres de chaque composante à l’aide des paramètres Output Eigenvalues Table (Tableau de valeurs propres en sortie) et Output Eigenvectors Table (Tableau de vecteurs propres en sortie), le tableau de vecteurs propres en sortie comprenant un diagramme à barres affichant les chargements de chaque composante. Pour la totalité des détails mathématiques de la LDA, consultez la section Ressources supplémentaires.
Détermination du nombre de composantes
L’un des choix les plus importants dans la réduction de dimension est celui du nombre de composantes à créer. Cela revient à choisir le nombre de dimensions des données en entrée à réduire. Vous pouvez parfois connaître le nombre de composantes dont vous avez besoin en fonction de l’analyse prévue (une méthode de Machine Learning dont l’efficacité se limite à un maximum de quatre variables, par exemple). Dans d’autres cas, vous pouvez utiliser autant de composantes principales dont vous avez besoin pour maintenir, par exemple, 90 pour cent de la variance totale des données d’origine. Dans d’autres cas encore, vous pouvez opter pour un équilibre entre réduction maximale du nombre de composantes et optimisation du pourcentage de variance maintenue.
Dans les deux méthodes de réduction des données, pour les champs d’analyse p, le pourcentage de variance expliqué par la ième composante est  , où di est la valeur propre de la ième composante. Chaque composante séquentielle conserve un plus petit pourcentage de la variance totale que la composante qui la précède.
, où di est la valeur propre de la ième composante. Chaque composante séquentielle conserve un plus petit pourcentage de la variance totale que la composante qui la précède.
Le nombre de composantes utilisées par l’outil dépend des valeurs spécifiées dans les paramètres Minimum Number of Components (Nombre minimal de composantes) et Minimum Percent Variance to Maintain (Pourcentage minimal de variance à maintenir).
- Si un paramètre est spécifié et pas l’autre, la valeur du paramètre spécifié détermine le nombre de composantes. Le nombre de composantes est égal au nombre le plus petit nécessaire pour satisfaire à la valeur minimale spécifiée.
- Si les deux paramètres sont spécifiés, le plus grand des deux nombres obtenus de composantes est utilisé.
- Si aucun des paramètres n’est spécifié, le nombre de composantes est déterminé en utilisant plusieurs méthodes statistiques, et l’outil utilise le plus grand nombre de composantes recommandé par chacune des méthodes. Les deux méthodes de réduction de dimension incluent la méthode du bâton brisé et l’essai de sphéricité de Bartlett. Pour l'ACP, un test de permutation est également réalisé si la valeur du paramètre Nombre de permutations est supérieure à zéro. Les résultats des essais statistiques s’affichent en tant que messages de géotraitement. Les détails mathématiques des trois essais peuvent être consultés dans la section Ressources supplémentaires.
Le tableau des valeurs propres en sortie s’accompagne d’un diagramme linéaire personnalisé, appelé un diagramme d’éboulis, qui montre le pourcentage de variance maintenu par chaque composante. Dans le diagramme d’éboulis ci-dessous, l’axe x montre chaque composante séquentielle, la ligne rouge indiquant le pourcentage de variance expliqué par chaque composante. La ligne rouge diminue, ce qui indique que chaque nouvelle composante maintient moins de variance que la composante précédente. La ligne noire verticale au-dessus de la composante 2 sur l’axe x indique que l’outil a utilisé deux composantes, et quelles ont maintenu 95,8 pour cent de la variance totale des variables d’origine. La ligne bleue montre les résultats de la méthode du bâton brisé utilisée pour estimer le nombre optimal de composantes. Le nombre optimal de composantes correspond souvent à l’intersection de la ligne rouge et de la ligne bleue, indiquant un accord quant au nombre de composantes.

Pratiques conseillées et limitations
Considérez ce qui suit lorsque vous utilisez cet outil :
- Pour la PCA, les résultats de cette analyse dépendent de la lise à l’échelle ou pas des variables. La PCA partitionnant la variance totale en composantes, plus les valeurs brutes d’un champ d’analyse sont importantes, plus le pourcentage de la variance totale qui lui est associée est élevé. La mise à l’échelle de chacun des champs d’analyse pour obtenir une variance égale à un annule cet effet. Par exemple, si les champs d’analyse sont mis à l’échelle, les données mesurées en pieds et celles mesurées en mètres donnent les mêmes composantes. En l’absence de mise à l’échelle, les données mesurées en pieds contribuent dans une plus large mesure à la première composante que les mêmes données en mètres. En effet, une valeur de distance en pieds est plus importante que la même valeur de distance mesurée en mètres (1 mètres = 3,2808 pieds).
- La PCA estime les valeurs propres et les vecteurs propres en prenant pour hypothèse que les relations entre tous les champs d’analyse sont linéaires. Si les relations entre les champs d’analyse ne sont pas linéaires, la PCA ne capture pas précisément ces relations. Il est recommandé de créer une matrice de nuages de points de vos variables d’analyse et de rechercher les modèles non linéaires. Si des modèles non linéaires sont trouvés, l’outil Transformer les champs peut être en mesure de linéariser les relations.
Ressources supplémentaires
Pour plus d’informations sur l’analyse en composantes principales (ACP) et l’analyse linéaire discriminante (ALD), consultez la référence suivante :
- James, G., Witten, D., Hastie, T., Tibshirani, R. (2014). « An Introduction to Statistical Learning: with Applications in R. » Springer Publishing Company, Incorporated. https://doi.org/10.1007/978-1-4614-7138-7
Pour plus d’informations sur les modes de calcul du nombre de composantes, consultez la référence suivante :
- Peres-Neto, P., Jackson, D., Somers, K. (2005). « How many principal components? Stopping rules for determining the number of non-trivial axes revisited. » Computational Statistics & Data Analysis. 49.4: 974-997. https://doi.org/10.1016/j.csda.2004.06.015.
Rubriques connexes
Vous avez un commentaire à formuler concernant cette rubrique ?