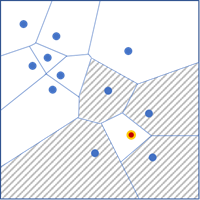
[近傍要約統計量 (Neighborhood Summary Statistics)] ツールは、1 つ以上のポイントの数値フィールドまたは近傍を使用したポリゴン フィーチャのローカル要約統計量を計算します。ローカル統計量としては、平均値、中央値、標準偏差、四分位範囲、歪度、分位数不均衡があります。近傍としては、距離バンド、近傍数、ポリゴン隣接、空間ウェイト ファイルがあります。すべてのローカル統計量は、カーネルを使用して地理空間的に加重できます。
![[近傍要約統計量 (Neighborhood Summary Statistics)] ツールの図 [近傍要約統計量 (Neighborhood Summary Statistics)] ツールの図](GUID-7F9D2BFB-10CF-4B3E-A9E7-E58E2D966F9B-web.png)
近傍タイプ
[近傍タイプ] パラメーターには、フォーカル フィーチャの近傍として使用するフィーチャを定義するのに使用できる 6 つのオプションがあります。
- [距離バンド] - 指定の距離 (最大 1,000) 内のすべてのフィーチャを近傍として使用します。デフォルトの距離は最短距離であり、各フィーチャに 1 つ以上の追加の近傍があることが保証されます。
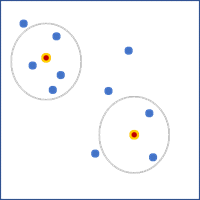
- [近傍数] - 最近接フィーチャの固定数が近傍として使用されます。
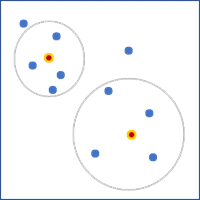
- [隣接エッジのみ] - フォーカル フィーチャとエッジを共有するポリゴンが近傍として使用されます。この方法はポリゴン フィーチャの場合のみ適用できます。
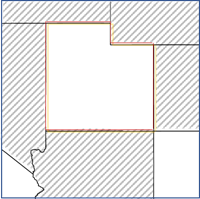
- [隣接エッジ コーナー] - フォーカル フィーチャとエッジまたはコーナーを共有するポリゴンが近傍として使用されます。この方法はポリゴン フィーチャの場合のみ適用できます。
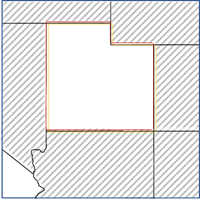
- [ドロネー三角形分割] - ドロネー三角形分割でエッジまたはコーナーを共有することで定義される近傍です。このオプションを使用すると、[ティーセン ポリゴンの作成 (Create Thiessen Polygons)] ツールをポイントで使用し、[隣接エッジ コーナー] オプションをティーセン ポリゴンで使用するのと同じになります。この方法はポイント フィーチャの場合のみ適用できます。
- [空間ウェイトをファイルから取得] - [ウェイト マトリックス ファイル] パラメーターに指定された空間ウェイト マトリックス ファイルで定義される各フィーチャの近傍とウェイトです。[空間ウェイト マトリックスの生成 (Generate Spatial Weights Matrix)] および [ネットワーク空間ウェイトの生成 (Generate Network Spatial Weights)] ツールでファイルを作成できます。
要約統計量
分析フィールドごとに計算できる 6 つの要約統計量があります。[ローカル要約統計量] パラメーターで指定します。この 6 つの要約統計量としては、中心性のメジャー値、可変性と拡散のメジャー値、対称性のメジャー値があります。各クラスには 2 つの統計量があり、1 つはトラディショナル、1 つはロバストです。ロバスト統計量とは、少数の外れ値の影響を受けない統計指標です。
分析フィールドの 6 つの統計量の計算には、デフォルトでは [ローカル要約統計量] パラメーターの [すべて] のオプションが使用されます。各統計量の計算式は、「ローカル統計量の計算式」 セクションをご参照ください。
中心性のメジャー値は、値の分布の中央または中心を推定するために使用されます。これらのオプションを使用して、ノイズ データの値をスムージングすることができます。中心性のメジャー値は、次のとおりです。
- [平均値] (トラディショナル) - 分析フィールドの値の算術演算平均値。
- [中央値] (ロバスト) - 50 番目のパーセンタイル。値の半分は中央値を下回り、半分は中央値を上回ります。
可変性と拡散のメジャー値は、可能性の高い値の分布範囲を推定するために使用されます。これらのオプションを使用して、分析フィールドの可変性がマップ全体で同様かどうか (分散定常性)、あるいは特定のエリアのローカル変動が他のエリアより高くなっているかどうかを調査することができます。可変性のメジャー値は、次のとおりです。
- [標準偏差] (トラディショナル) - 分析フィールドの値の標準偏差。
- [四分位範囲] (ロバスト) - 分析フィールドの値の中央の範囲 (75 番目のパーセンタイルから 25 番目のパーセンタイルを減算)。データの半分はこの範囲内に収まります。
対称性のメジャー値は、分布の形状が中央付近で対称的かどうかを計測するために使用されます。これらのオプションを使用して、高い/低い極値の頻度を調査することができます。対称性のメジャー値は、次のとおりです。
- [歪度] (トラディショナル) - 分析フィールドの値の歪度。
- [分位数不均衡] (ロバスト) - 25 番目と 75 番目のパーセンタイルを基準にした中央値の位置を示す -1 ~ 1 の範囲の値。-1 に近い値の場合、中央値が 25 番目のパーセンタイルに近いことを示し、1 に近い値の場合、75 番目のパーセンタイルに近いことを示します。0 に近い値の場合、中央値が 25 番目と 75 番目の中間となっていて対称的であることを示します。
ツールの出力
出力フィーチャは、最初の分析フィールド (分析フィールドが入力されていない場合は近傍までの距離) を計算した [ローカル要約統計量] パラメーターで指定された統計量を使用して、マップ内でシンボル表示されます。ローカル要約統計量の [すべて] を選択すると、フィーチャは [平均値] の統計量を表示します。その他のすべての分析フィールド要約統計量は、すべての分析フィールドのコピーとともに出力フィーチャにフィールドとして保存されます。分析フィールドごとに使用される近傍の数を示すフィールドもあります。
地理空間加重要約統計量
[近傍タイプ] パラメーターを [距離バンド] または [近傍数] として指定すれば、すべての統計量を [ローカル加重方式] パラメーターを使用して地理空間的に加重することができます。[近傍タイプ] パラメーターに [空間ウェイトをファイルから取得] を指定した場合、ファイルで指定されたウェイトが加重方式として使用されます。加重方式を適用するとすべての要約統計量が加重され、フォーカル フィーチャに近い近傍ほどカーネルと呼ばれる関数を使用した計算で受け取るウェイトは大きくなり、フォーカル フィーチャからの距離とともに小さくなります。[ローカル加重方式] パラメーターでは 2 つのカーネル関数が提供されています。
- Bisquare
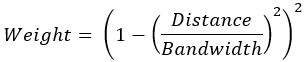
- Gaussian
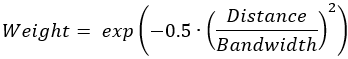
カーネル関数は、ウェイトが距離に伴って減少する速度を制御するバンド幅によって決まります。各カーネルのバンド幅は、[カーネル バンド幅] パラメーターで指定します。値を指定しなかった場合、デフォルト値は実行時に計算され、ジオプロセシング メッセージとして表示されます。デフォルトのバンド幅の計算方法については、「カーネル密度の詳細」をご参照ください。
注意:
距離バンドの近傍の場合、代わりに [距離バンド] パラメーターと同じ値がカーネル バンド幅のデフォルト値となります。
ローカル統計量の計算式
このセクションでは、1 つのフォーカル フィーチャのすべての要約統計量の計算式について、加重されたバージョンと加重されないバージョンを説明します。これらの計算式は、すべての分析フィールドのすべての入力フィーチャに適用されます。
すべての式で、i = 1, ..., n とは、値 (xi) によって昇順で並べ替えられたフォーカル フィーチャの近傍 (フォーカル フィーチャそのものを含む場合もある) のことを指します。すべてのウェイト (wi) は、これらの式を適用する前に合計が 1 となるよう正規化されます。各統計量の加重されないバージョンは、wi = 1/n をすべての近傍 i に設定した値となります。
トラディショナル統計量
次の表では、各トラディショナル統計量について、加重されたバージョンと加重されないバージョンの計算式を示しています。
| 統計 | 加重された計算式 | 加重されない計算式 |
|---|---|---|
平均 | 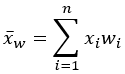 | 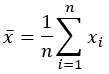 |
標準偏差 | 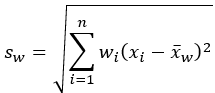 | 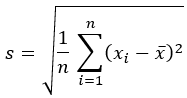 |
歪度 | 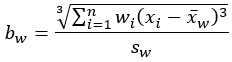 | 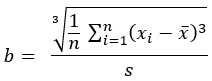 |
ロバスト統計量
すべてのロバスト統計量は、加重された p 分位数の定義によって決まります。p は、0 ~ 1 の値を取ります。この定義は、加重中央値 (p=0.5)、第 1 四分位値 (p=0.25)、第 3 四分位値 (p=0.75) を計算するために使用されます。指定された p の p 分位数は、次のように定義されます。
- 加重された分位数 p
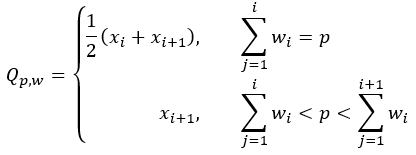
- 加重されない p 分位数
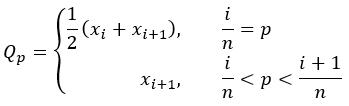
次の表では、上記の p 分位数の定義を使用して、各ロバスト要約統計量の加重されたバージョンと加重されないバージョンの計算式を示しています。
| 統計 | 加重された計算式 | 加重されない計算式 |
|---|---|---|
中央値 | 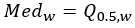 | 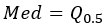 |
四分位範囲 | 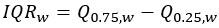 | 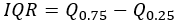 |
分位数不均衡 | 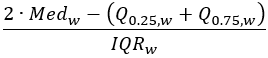 | 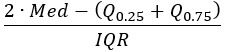 |
参考資料
地理空間加重要約統計量の詳細については、次の資料をご参照ください。
- Brunsdon, C., Fotheringham, A.S., Charlton, M. (2002). "Geographically weighted summary statistics — a framework for localised exploratory data analysis." Computers, Environment and Urban Systems, 26(6): 501-524. ISSN 0198-9715. https://doi.org/10.1016/S0198-9715(01)00009-6.