時系列データの外れ値は、その時系列の他の値のパターンおよび傾向と著しく異なる値です。たとえば、休日前後のオンラインショッピングや豪雨時の交通事故の高い件数は、時系列の外れ値として検出される可能性があります。数値の小数部分の欠落などの単純なデータ入力エラーも、よくある外れ値の原因の 1 つです。時系列予測における外れ値の特定は重要です。外れ値は、将来値の予測に使用される予測モデルに影響するからです。位置の時系列に外れ値がわずかな数でも存在すれば、予測の精度および信頼性が下がる可能性があります。外れ値の位置、特に時系列の最初または最後の方にある外れ値は、誤った予測になる可能性があります。そのような位置の特定は、各位置の予測値をどう信頼するかを判断する助けになります。
[外れ値オプション] パラメーターの [外れ値の識別] オプションを指定し、[カーブ フィット予測 (Curve Fit Forecast)]、[指数平滑法予測 (Exponential Smoothing Forecast)]、[フォレストベース予測 (Forest-based Forecast)] ツールを使用することで、時空間キューブの位置ごとに外れ値を特定できます。
外れ値の視覚化と探索
外れ値を特定するオプションを使用して予測ツールの 1 つを実行すると、検出された外れ値についての情報は、出力フィーチャ シンボル、時系列チャート、出力時空間キューブの 2D または 3D ビジュアライゼーション、ジオプロセシング メッセージで提供されます。
ポップアップ チャート
マップの出力フィーチャをクリックすると、時系列モデルと予測モデルを表示する [ポップアップ] ウィンドウでポップアップ チャートが生成され、特定された外れ値は大きいポイントとして表示されます。次の図は、外れ値が 1 つ特定されたフィーチャの時系列を示しています。
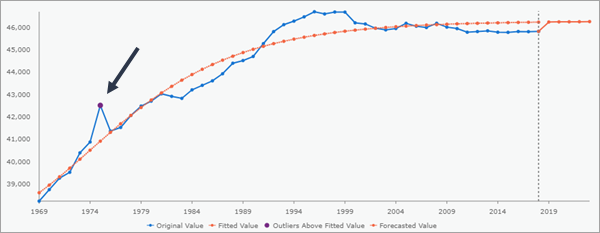
時空間キューブの視覚化
時空間キューブの外れ値は、[表示テーマ] パラメーターの [時系列外れ値の結果] オプションを使用した [時空間キューブを 2D で視覚化 (Visualize Space Time Cube in 2D)] および [時空間キューブを 3D で視覚化 (Visualize Space Time Cube in 3D)] ツールで 2D と 3D で視覚化および探索されます。
2D フィーチャ出力の場合、出力フィーチャは位置ごとに外れ値の数でシンボル化されます。時系列と督励された外れ値を表示するポップ チャートを含みます。
3D フィーチャ出力の場合、出力チャートには特定された外れ値の位置と時間が 3D シーンで表示されます。値が時系列外れ値として特定された時空間ビンには、値が予測モデルの適合値より上か下かによって、[適合値より上] または [適合値より下] のラベルが付きます。適合値の上の外れ値は紫、適合値より下の外れ値は緑で表示されます。外れ値として特定されていない時空間ビンには、[外れ値ではない] のラベルが付き、ライト グレーで表示されます。
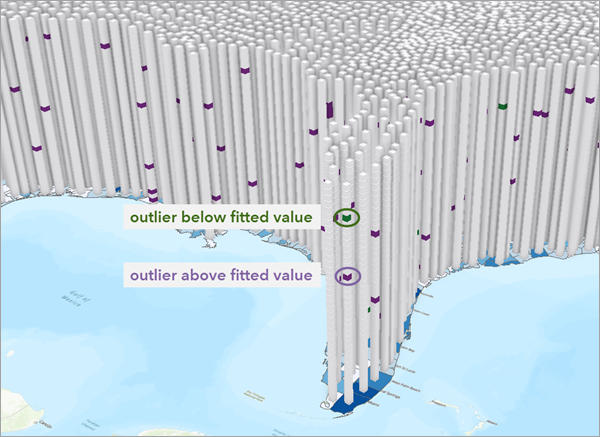
また、3D フィーチャには 2 つのチャートがあります。[3D 視覚化時系列] チャートには、時空間キューブの時間ステップ全体の時系列の平均値を表すライン プロットが表示されます。このチャートは、[表示テーマ] パラメーターの [予測結果] オプションでも作成できますが、その場合外れ値の検知に関する情報は含まれません。
2 つ目のチャートは、[時間経過に伴う適合値より上または下の外れ値の数] チャートです。このチャートは、時空間キューブの時間ステップごとに適合値より上の外れ値と下の外れ値の合計数を表示する積み上げバー チャートです。これにより、多数の外れ値が発生した重要な日付を特定でき、これらの日付の値は異常に高かったのか低かったのかを確認することもできます。
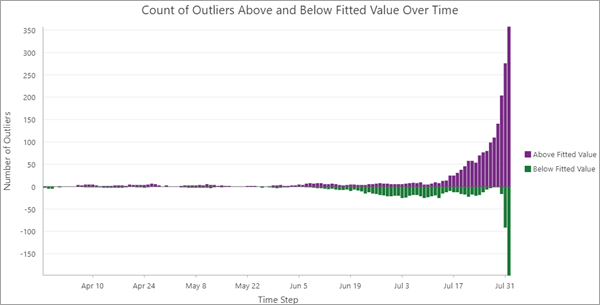
ジオプロセシング メッセージ
ジオプロセシング メッセージには、[時系列の外れ値サマリー] セクションがあります。このセクションの最初の部分には、最低 1 つの外れ値を含む位置の数と割合が表示されます。これにより、予測モデルの時系列全体への適合度を簡単に確認できます。2 番目の部分には、位置ごとと時間ステップごとの外れ値の数の要約統計量 (最小、平均、最大) が表示されます。これにより、個々の位置と個々の時間ステップの外れ値の発生頻度を調査することができます。このセクションには、外れ値の数が最も多い時間ステップも表示されます。これを使用して、多数の外れ値が発生した重要な日付を特定することができます。

コンテキスト外れ値とグローバル外れ値
ツールで検知できる時系列外れ値にはいくつかのタイプがあります。すべてのタイプは同じ方法で検知されますが、各タイプを理解することで、特定の時間ステップが外れ値として特定され、他の時間ステップは特定されなかった理由を明確にすることができます。
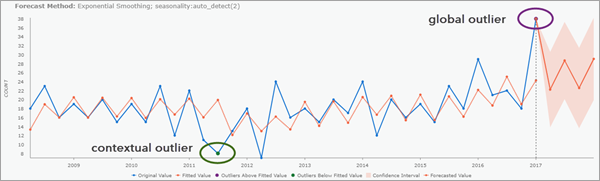
最もシンプルなタイプはグローバル外れ値で、生の値が他の値よりも著しく大きいまたは小さいものです。こうした外れ値は、多くの場合異常値や休日などの特別なイベントに該当します。下のチャートには、グローバル外れ値が表示されています。特定された外れ値は、時系列の他の日よりも値が著しく高く、そのために外れ値として特定されています。
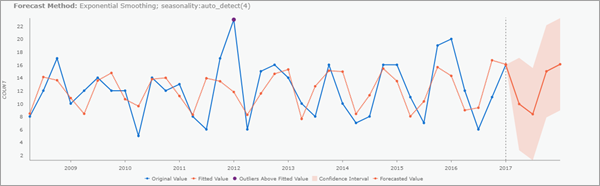
なお、必ずしも時系列で最大もしくは最小でないと外れ値を宣言できないわけではありません。その代わり、時系列のパターンと傾向に基づいて予想される値よりも著しく高いもしくは低い値を持っていれば、コンテキストに応じて外れ値を特定できる場合もあります。予測モデルは、こうしたパターンと傾向を組み込むことで、コンテキスト外れ値を特定するベースラインの役割を果たします。たとえば、年平均気温の時系列について考えてみましょう。この数十年で平均気温は上昇しているので、気温の適合予測モデルも、この上昇を反映して上昇します。これは、1950 年に典型的と見なされて外れ値とは判定されない気温が、2020 年には外れ値と見なされる可能性があるということです。つまり、1950 年の典型的な気温は、2020 年の基準では低いと見なされます。
下のチャートの時系列には、コンテキスト外れ値とグローバル外れ値の両方が表示されています。コンテキスト外れ値の値は時系列の最小値ではありませんが、オレンジで示された予測モデルを大きく下回っているため、低い値の外れ値として特定されています。
値が外れ値に特定されるかどうかは、予測モデルが時系列に適合している度合いにもよります。予測モデルが時系列データの近くにおおむね適合している場合は、予測モデルからわずかに外れているだけの値であっても外れ値として特定できます。同様に、予測モデルが時系列データにあまり適合していない場合は、予測モデルから大きく外れていても外れ値として特定されない可能性があります。
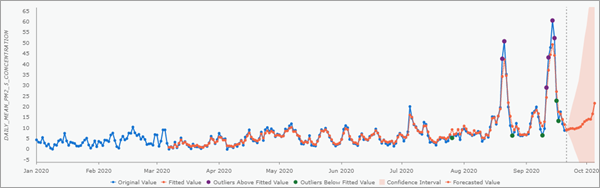
下のチャートには、外れ値として特定されたさまざまな値が表示されています。こうした値は、オレンジで示された予測モデルから大きく外れているようには見えませんが、時系列の他の値よりは大きく外れています。
時系列外れ値向けの Generalized ESD テスト
Generalized ESD (Extreme Studentized Deviate) テストは、時空間キューブの位置ごとの外れ値の存在をテストするために使用されます。このテストは 1 つのテストではなく一連のテスト群 (それぞれをグラブス検定と言います)であり、各テストは指定された信頼度で特定の数の外れ値をチェックします。最初のテストは、データセットに外れ値が正確に 1 つ存在することをチェックします。2 番目のテストは、外れ値が正確に 2 つ存在することをチェックします。3 番目のテストは、正確に 3 つ存在することをチェックします。これを [外れ値の最大数] パラメーター (デフォルトは時間ステップ数の 5 パーセント、端数は切り捨て) の値まで繰り返します。その後、統計的に有意な外れ値の最大数に関連付けられた外れ値を返します。たとえば外れ値の最大数を 3 とすると、1 つの外れ値のテストは統計的に有意、2 つの外れ値のテストは統計的に有意でない、3 つの外れ値のテストは統計的に有意である場合、このツールは 3 つの外れ値を返します。同様に、1 つの外れ値のテストは統計的に有意、2 つの外れ値のテストは統計的に有意、3 つの外れ値のテストは統計的に有意でない場合、このツールは 2 つの外れ値を返します。
T 個の適合した時間ステップを持つ時系列の場合、テストは次のように進みます。なお、i の範囲は 1 から外れ値の最大数までです。
- 生の値から予測モデルの値を減算し、時間ステップ t ごとに残差を計算します :
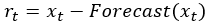
- 残差の平均値と標準偏差を計算します。
- 平均値から出した最大絶対偏差を標準偏差で除算することで、検定統計量を計算します :
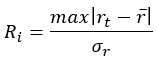
- 検定統計量を次の臨界値と比較します :
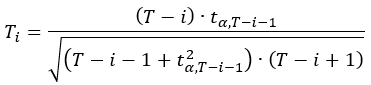 。ここでは t α,T-i-1 は信頼度 (1 - α / (2(T-i+1))) での自由度 T-i+1 を持つ t 分布の両側臨界値であり、α は有意水準です (信頼度によって決まる)。
。ここでは t α,T-i-1 は信頼度 (1 - α / (2(T-i+1))) での自由度 T-i+1 を持つ t 分布の両側臨界値であり、α は有意水準です (信頼度によって決まる)。 - 検定統計量が臨界値よりも大きい場合、正確に i つの外れ値のテストは統計的に有意となります。
- 最大絶対残差に関連付けられた値を削除し、未削除のすべての時間ステップで手順 2 ~ 5 を繰り返したうえで、i を 1 ずつ増やします。残差の平均値と標準偏差は、繰り返すたびに値が削除されることで変化します。この平均値と標準偏差の再計算により、予測モデルにおける外れ値の影響を補正します。
- 統計的に有意だった外れ値の最大数に関連付けられた外れ値を返します。
このテストは時空間キューブの位置ごとに独立して実行されるため、位置が異なれば指定される外れ値の数も異なる可能性があります。位置ごとの外れ値の数は、出力フィーチャの Number of Model Fit Outliers フィールドで確認できます。
ベスト プラクティスおよび制限
時系列外れ値を特定する場合、いくつかの重要な検討事項および制限事項があります。
- [フォレストベース予測 (Forest-based Forecast)] ツールを使用している場合、[時間ステップ ウィンドウ] パラメーターを空のままにして各場所で異なる時間ステップ ウィンドウを評価するのではなく、値を指定することをお勧めします。各場所で、フォレスト モデルは最初の時間ステップ ウィンドウの値を使用して予測モデルをトレーニングします。外れ値は、残りの時間ステップについてのみ検出されます。別の場所で異なる数の時間ステップがフォレストのトレーニングから除外されると、時間ステップごとまたは場所ごとの外れ値の平均数、最小数、最大数が誤った結果になる可能性があります。
- Generalized ESD テストでは、近似値を用いて臨界値を推定します。こうした近似値は、最低 25 の時間ステップのある時系列の場合が最も正確となります。
- 異なる予測モデルと予測ツールを使用すると、外れ値として特定される時間ステップが異なる場合があります。時系列の値に最も適合した予測モデルに対する外れ値のみを検出するようお勧めします。
参考資料
Generalized ESD テストおよびグラブス検定の詳細については、次の資料をご参照ください。
- Grubbs, F. (1950). "Sample Criteria for Testing Outlying Observations." Annals of Mathematical Statistics 21(1):27–58. https://doi.org/10.1214/aoms/1177729885
- Rosner, B. (1983). "Percentage Points for a Generalized ESD Many-Outlier Procedure." Technometrics 25(2):165-172.
関連トピック
- 時空間パターン マイニング ツールボックスの概要
- 時系列予測ツールセットの概要
- カーブ フィット予測 (Curve Fit Forecast)
- 指数平滑法予測 (Exponential Smoothing Forecast)
- 位置による予測評価 (Evaluate Forecasts By Location)
- フォレストベース予測 (Forest-based Forecast)
- カーブ フィット予測 (Curve Fit Forecast) の詳細
- 指数平滑化予測 (Exponential Smoothing Forecast) の概要
- フォレストベースの予測の概要
- フォレストベースの分類と回帰 (Forest-based Classification and Regression)
- フォレストベースの分類と回帰分析 (Forest-based Classification and Regression) の詳細