属性の不確実性に対する感度の評価の詳細

[属性の不確実性に対する感度の評価 (Assess Sensitivity to Attribute Uncertainty)] ツールは、1 つ以上の分析変数 (属性) の値が不確実である場合に、空間統計ツールボックス内の一部のツールの分析結果がどのように変化するかを評価します。 属性の不確実性は、許容誤差、上限と下限、元の値の指定されたパーセンテージを使用して指定できます。 このツールは、次のツールからの出力フィーチャを受け取ります。

• ホット スポット分析 (Hot Spot Analysis (Getis-Ord Gi*))
• 最適化ホット スポット分析 (Optimized Hot Spot Analysis)
• クラスター/外れ値分析 (Cluster and Outlier Analysis (Anselin Local Moran's I))
• 最適化外れ値分析 (Optimized Outlier Analysis)
• 一般化線形回帰分析 (Generalized Linear Regression)
• 空間的自己相関分析 (Spatial Autocorrelation (Global Moran's I))

このツールは、元の分析変数とその不確実性の尺度を使用し、新しいデータを繰り返しシミュレートすることで、感度分析を実行します。 その後、シミュレートされたデータを使用して元の分析ツールを何度も再実行し、結果を要約します。 シミュレーションの結果が元の結果とよく似ている場合、元の結果が堅牢で信頼性が高いことを確信できます。 ただし、シミュレーションが元の結果と大きく異なっている場合、元の結果から積極的に強力な結論を導くのは避けてください。

適用例

このツールには次のような適用例があります。

• ある地域の慈善団体がホット スポット分析を使用し、貧困を削減するサービスを優先的に受ける郡内のエリアを特定する。 分析により、貧困のクラスタリングが非常に高い地域 (99% の信頼度を持つホット スポット) に焦点を当てようとしています。 ホットスポットがどのように変化するかを監視することで、サービスの優先度の強化と再考のきっかけとなる可能性があります。
• 大手小売チェーンが、年齢や可処分所得などの人口統計的要因がスポーツ用品の売上にどれだけの影響を及ぼすかを推定するために、一般化線形回帰モデルを策定しました。 調査によって収集された説明変数には、上限と下限が含まれます。 これらの変数に不確実性を組み込むことで、小売業者は販売数量の潜在的な範囲を探ることができます。

属性の不確実性

属性の不確実性とは、データ収集や集約において自然かつ不可避な側面から生じるデータ値の可変性 (サンプリング誤差や測定誤差など) を指します。 サンプリング誤差は、母集団のサブセットからデータを収集する場合に発生するもので、サンプルが母集団全体をどの程度正確に表しているかという疑問を呈します。 測定誤差は、温度計や風速計などのデータ収集装置によって記録された値に、真値と比べてわずかな差異が見られる場合に発生します。 多くの場合、データは、測定の真値の最良推定値 (点推定と呼ばれる) と、不確実性の度合いの測定とともに提供されます。 不確実性の要因はデータの精度を左右する場合がありますが、このような要因は現実世界のデータ収集プロセスには必ず存在します。 属性の不確実性と、分析結果に対する影響を認識し、それを探索することで、分析の透明性と堅牢さを高めることができます。

不確実性の定量化

このツールでは、許容誤差、上限と下限、属性値の上限パーセンテージと下限パーセンテージの 3 つの方法で属性の不確実性を指定します。

許容誤差

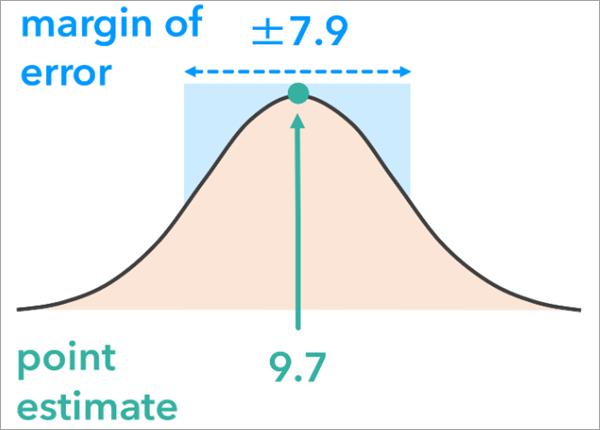
許容誤差は、属性の真値が含まれる可能性が高い範囲を表します。 これは信頼度 (90% など) に関連しており、属性の実際の値が推定によって定義された範囲内から上下の許容誤差に収まっていることを確信できる度合いを示します。 たとえば、ある郡において実施された調査では 2,500 人が貧困層と推定され、90% 信頼度の許容誤差は 300 であるとします。 これは、貧困に苦しむ人数の真値が 2,200 ～ 2,800 の間である可能性が 90% であることを意味します。 この方法を使用する場合、少なくとも 1 つの分析変数に対して許容誤差フィールドが必要になります。 このフィールドには、真の人口の値がサンプル推定値からどの程度上下にずれるかを表す、数値の誤差範囲が含まれます。 信頼度はデフォルトで 90% ですが、[許容誤差の信頼度] パラメーターを使用して調整できます。

注意:

通常、許容誤差は、元の変数の隣にフィールドとして記録されます。 これは、米国国勢調査局の ACS (American Community Survey) の ArcGIS Living Atlas of the World データの多数の変数に見られます。 多くの国家統計機関が、不確実性に関する同様の尺度を提供しています。

上限と下限

上限と下限は、推定値周辺の範囲を明示的に指定することで、属性の不確実性を表します。 上限と下限は、誤差とは異なり、点推定周辺で対称である必要はありません。

上下のパーセント

上下のパーセントのオプションは、各フィーチャの元の属性値を所定のパーセンテージで調整することで、属性の不確実性を表します。 これにより、推定値の周辺に真値を含む可能性がある範囲が作成されます。 このアプローチは、許容誤差や上限と下限などの他の方法では不確実性を表せない場合に便利です。

注意:

属性の不確実性をフィーチャごとに指定できる許容誤差や上限と下限のオプションとは異なり、上下のパーセントのオプションではすべてのフィーチャに対して同じ不確実性の定義を適用します。

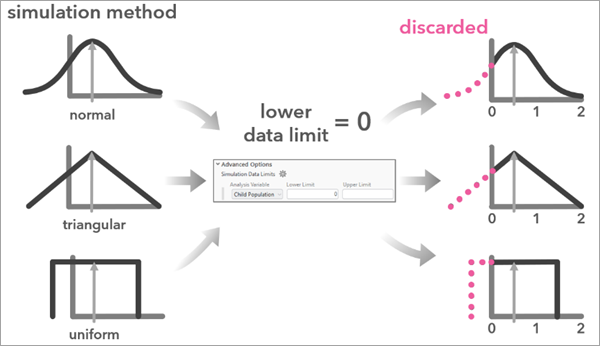
シミュレーションを使用した不確実性への対処

このツールは、不確実性に対する分析結果の感度を評価するために、元の分析変数とその不確実性の尺度に基づいてシミュレートされたデータセットを生成します。 理想的には、シミュレートされたデータセットは、実世界に存在しうるデータの妥当なバージョンを表します。 さらに、真値が点推定を中心にどのように配置されるか、あるいは点推定からどのように広がるか、さまざまな仮定があります。 このツールでは、確率分布を使ってシミュレートされたデータ値を制限し、データの範囲と実現の尤度を把握します。 サポートされる分布は、正規、三角、一様です。 一般化線形回帰分析のデータをシミュレートする場合、説明変数間の相関構造は維持されます。 他のツールによる分析結果では、データは各フィーチャとは別にシミュレートされます。 説明変数間の従属性を考慮するため、これらの相関はグローバルに推定され、各フィーチャのシミュレートされた値は、平均ゼロと、説明変数間のグローバル相関に基づく共分散行列を持つ、多変量正規分布のランダム ノイズを追加することで生成されます。 ランダム ノイズは多変量正規分布に基づいているため、一般化線形回帰分析のシミュレーションでは、正規シミュレーション法のみがサポートされます。

正規

通常、[シミュレーション法] パラメーターの [正規] オプションは、信頼度が関連付けられた許容誤差がある場合に使用されます。 このオプションでは、元の分析変数の値に等しい平均と、フィーチャの許容誤差の値と信頼度に基づく標準偏差を持つ正規 (またはガウス) 確率分布を使用します。

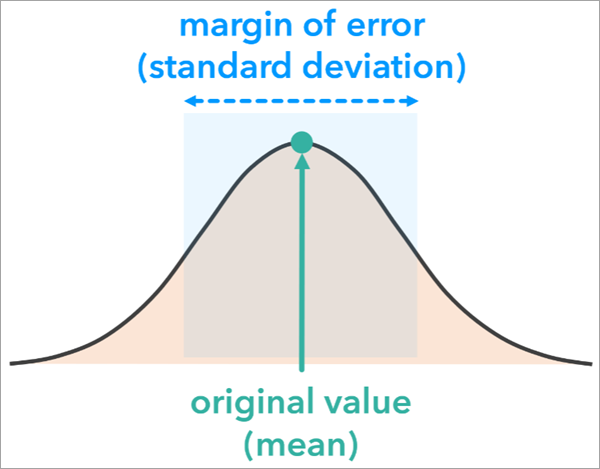
確率分布の形状が示すように、元の推定値に近い値は、遠い値よりも生成される可能性が高くなります。 しかし、これは許容誤差によって大きく異なります。 許容誤差が大きい場所 (サンプル サイズが小さい場合が多い) は裾が長い分布になります。つまり、シミュレーションは元の推定から離れた値を生成する可能性が高いことを意味します。

三角

三角分布は、元の値が真値の推定と考えられる場合によく使用されます。 [シミュレーション法] パラメーターの [三角] オプションは、値が推定値周辺に密集する可能性が高いが、広がりが非対称的となる、非対称分布において特に便利です。 三角分布は、最小データ値、フィーチャの元の値、最大データ値に基づいて各フィーチャのデータをシミュレートするために構築され、使用されます。 [不確実性タイプ] パラメーター値は、三角分布の最小データ値と最大データ値を決定します。

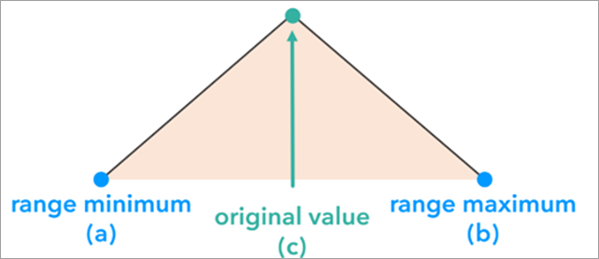
三角確率分布の形状により、分布の両極の値よりも元の値に近い値が生成される可能性が高くなります。

注意:

正規分布とは異なり、形状は対称的である必要はありません。 たとえば、下限と上限が異なることがあります。

一様

[シミュレーション法] パラメーターの [一様] オプションは、各位置の元の値が真値をあまり正確に推定しておらず、属性の不確実性について提供される唯一の情報は可能な値の範囲である場合に使用されます。 このオプションは、一様確率分布を、不確実性タイプによって設定された範囲の最小値、および不確実性タイプによって設定された範囲の最大値という 2 つのパラメーターとともに使用します。 正規分布や三角分布とは異なり、一様分布は確率分布パラメーターで元の値を使用しません。シミュレーションでは、最小値と最大値の間の各値が等しい確率で生成される可能性があります。

サポートされているツール

既存のレイヤーを入力として受け取るほとんどのジオプロセシング ツールとは異なり、このツールへの入力は空間統計ツールボックスの次のいずれかのツールの結果レイヤーです。

• ホット スポット分析 (Hot Spot Analysis (Getis-Ord Gi*))
• 最適化ホット スポット分析 (Optimized Hot Spot Analysis)
• クラスター/外れ値分析 (Cluster and Outlier Analysis (Anselin Local Moran's I))
• 最適化外れ値分析 (Optimized Outlier Analysis)
• 一般化線形回帰分析 (Generalized Linear Regression)
• 空間的自己相関分析 (Spatial Autocorrelation (Global Moran's I))

ホット スポット分析ツール、最適化ホット スポット分析ツール、クラスター/外れ値分析ツール、最適化外れ値分析ツール

[ホット スポット分析 (Hot Spot Analysis (Getis-Ord Gi*))] ツール、[最適化ホット スポット分析 (Optimized Hot Spot Analysis)] ツール、[クラスター/外れ値分析 (Cluster and Outlier Analysis (Anselin Local Moran's I))] ツール、[最適化外れ値分析 (Optimized Outlier Analysis)] ツールの結果では、分析を繰り返し実行する中でフィーチャがカテゴリを変更した頻度を確認することで安定性が評価されます。 たとえば、フィーチャが元の分析で 90% の信頼度を持つホット スポットで、シミュレーション データを使用した分析の中で他のカテゴリに変更された場合、カテゴリ変更としてカウントされます。 ツールは、フィーチャのカテゴリ変更の回数をカウントします。 シミュレーションの 80% 以下が元のカテゴリとなった場合は、フィーチャは不安定としてマークされます。

ツールは、不安定性レイヤーを含むグループ レイヤーと、元の分析結果のコピーを生成します。

さらに、グループ レイヤーには、元の分析の各カテゴリと各主要カテゴリのフィーチャ数を表示するチャートが含まれます。 主要カテゴリとは、各位置においてツールを繰り返し実行したすべての結果で、最も頻繁に発生したカテゴリです。

このチャートは、カテゴリの不安定性のパターンを特定するのに役立ちます。 元の各カテゴリが主要カテゴリと完全一致する、完全に安定した結果はセル対角線を塗りつぶします。

注意:

このツールは、[最適化ホット スポット分析 (Optimized Hot Spot Analysis)] ツールまたは [最適化外れ値分析 (Optimized Outlier Analysis)] ツールを実行する際に、集約ポイントから得られた分析結果をサポートしません。

一般化線形回帰分析ツール

一般化線形回帰分析の不確実性を評価する際、[一般化線形回帰分析 (Generalized Linear Regression)] ツールの主な結果は、シミュレーション実行全体にわたる回帰診断の分布を示すチャートです (相関係数の二乗、説明変数の係数など)。 このツールは、元の分析結果のコピーを含むグループ レイヤー、元のツールの繰り返しの実行から得られた結果をまとめたテーブル、そして相関係数の二乗、Jarque-Bera 統計的有意性、標準化された説明変数の係数を示す 3 つのチャートを表示します。

空間的自己相関分析ツール

[空間的自己相関分析 (Spatial Autocorrelation (Global Moran's I))] ツールの結果に関して、ツールの目的は、既知の属性の不確実性においてグローバル空間的自己相関の元の評価がどの程度確実であるかを理解することです。 このツールは、元の分析結果のコピーを含むグループ レイヤー、ツールの繰り返しの実行から得られた結果をまとめたテーブル、そして Moran インデックス値とそれらの Z スコアの分布を示すチャートを表示します。

一般的に、Moran インデックス値とそれらの Z スコアのほとんどは、元の値よりも小さくなります。これは、データ値に無相関のランダム ノイズを追加すると、データの空間的自己相関が減少する傾向があるためです。

注意:

[空間的自己相関分析 (Spatial Autocorrelation (Global Moran’s I)] ツールは出力フィーチャを生成しません。 [空間的自己相関分析 (Spatial Autocorrelation (Global Moran’s I))] ツールで使用された元の入力フィーチャを、[分析結果フィーチャ] パラメーター値として使用します。

その他の注意事項

以下のサブセクションでは、その他の情報について説明します。

出力の安定性閾値の変更

[ホット スポット分析 (Hot Spot Analysis (Getis-Ord Gi*))] ツール、[最適化ホット スポット分析 (Optimized Hot Spot Analysis)] ツール、[クラスター/外れ値分析 (Cluster and Outlier Analysis (Anselin Local Moran's I))] ツール、[最適化外れ値分析 (Optimized Outlier Analysis)] ツールの結果では、不安定性レイヤーはデフォルトの安定性閾値である 80% を適用します。 つまり、あるフィーチャが安定していると見なされるには、そのフィーチャがシミュレーションの 80% 以上で元の分析と同じカテゴリになくてはなりません。 この閾値を大きくすると、より多くのフィーチャが不安定であると見なされ、この閾値を小さくすると、不安定であると見なされるフィーチャの数が少なくなります。

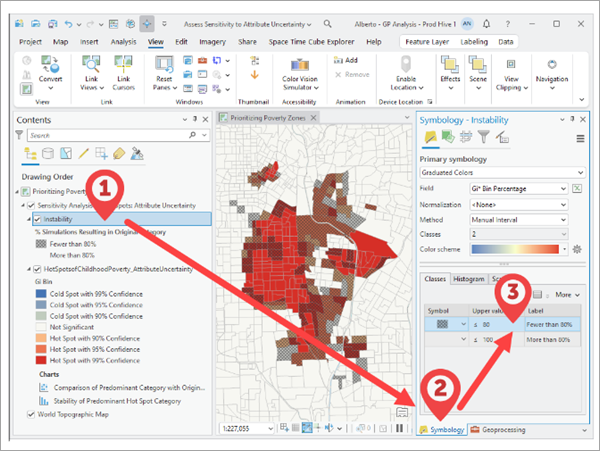
安定性を定義する閾値は、レイヤー シンボルの設定で構成できます。 閾値を変更するには、まず出力グループ レイヤーで不安定性レイヤーを特定し、選択する必要があります。 [シンボル] ウィンドウを開き、次に 80% クラスの [上限] 値のセルをダブルクリックして、閾値を編集します。

シミュレーション データの制限

分析変数のシミュレーション値の範囲の制限を設定できます。 これは、分析変数が負であってはならない場合や (個数)、ゼロから 100 の範囲でなくてはならない場合 (パーセンテージ) に役立ちます。 [シミュレーション データ制限] パラメーターを使用し、各変数に対して可能な値の範囲を設定します。 [シミュレーション データ制限] パラメーター値を指定すると、ツールは指定範囲外に生成されたシミュレーション値を破棄し、シミュレーションを繰り返します。

中間シミュレーション結果の保存

ツールが作成するシミュレーションは、フィーチャクラスとして保存できます。 [シミュレーション結果のワークスペース] パラメーターを使用し、ツールが各シミュレーション結果を保存する既存のワークスペースを設定します。

各ファイルの命名規則は、「分析結果フィーチャの名前 _ シミュレーション ID _ シミュレーションのタイム スタンプ」の形式に従います。 各シミュレーション結果フィーチャクラスには、元の分析結果のスキーマが含まれます。

中間シミュレーション結果は、さらに分析を行う場合に便利です。 たとえば、[一般化線形回帰分析 (Generalized Linear Regression)] ツールのシミュレーション結果のワークスペースを調べ、シミュレーション全体における予測値の分布の理解を深めることができます。

ジオプロセシング操作のメタデータ

分析ツール、入力フィーチャ、分析で使われる追加パラメーターを特定するため、ツールは [分析結果フィーチャ] パラメーター値からメタデータを読み取ります。 このため、分析結果フィーチャを生成した分析が、データセット メタデータに書き込むよう構成されている必要があります。

この設定はデフォルトでアクティブになっています。 この設定を確認するには、[オプション] ダイアログ ボックスを開き、[ジオプロセシング] タブをクリックし、[ログ] セクションでジオプロセシング操作をデータセット メタデータに書き込むオプションがオンになっていることを確認します。

注意:

このツールは、ホスト レイヤーで実行される [空間的自己相関分析 Spatial Autocorrelation (Global Moran’s I)] ツールをサポートしていません。これらのデータセットに対してメタデータを変更できないためです。

参考資料

詳細については、次のリソースをご参照ください。

• JingXiong Zhang and Michael Goodchild. 2002 "Uncertainty in Geographical Information." Taylor & Francis. ISBN 0-203-47132-6. https://doi.org/10.1201/b12624.
• Raphaella Diniz, Pedro O.S. Vaz-de-Melo, Renato Assunção. 2024. “Data augmentation for spatial disease mapping.” Spatial Data Science Symposium 2021 Short Paper Proceedings. https://doi.org/10.25436/E2KS35
• Michele Crosetto and Stefano Tarantola. 2001. "Uncertainty and sensitivity analysis: tools for GIS-based model implementation." International Journal of Geographical Information Science. 15:5, 415-437. https://doi.org/10.1080/13658810110053125
• Zhou Dimin. 2010. “Research on Propagation of Attribute Uncertainty in GIS.” 2010 International Conference on Intelligent Computation Technology and Automation.
• Hyeongmo Koo, Takuya Iwanaga, Barry F.W. Croke, Anthony J. Jakeman, Jing Yang, Hsiao-Hsuan Wang, Xifu Sun, Guonian Lü, Xin Li, Tianxiang Yue, Wenping Yuan, Xintao Liu, and Min Chen. 2020. “Position paper: Sensitivity analysis of spatially distributed environmental models- a pragmatic framework for the exploration of uncertainty sources.” Environmental Modelling and Software. https://doi.org/10.1016/j.envsoft.2020.104857
• Hyeongmo Koo , Yongwan Chun, and Daniel A. Griffith. 2018. “Geovisualizing attribute uncertainty of interval and ratio variables: A framework and an implementation for vector data.” Journal of Visual Languages and Computing 44 89-96. https://doi.org/10.1016/j.jvlc.2017.11.007
• Robert Haining, Daniel A. Grifith, and Robert Bennett. 1983. “Simulating Two-dimensional Autocorrelated Surfaces.” Geographical Analysis. https://doi.org/10.1111/j.1538-4632.1983.tb00785.x
• Sirius Fuller and Charles Gamble. 2020. "Calculating Margins of Error the ACS Way." American Community Survey (ACS) Programs and Surveys, U.S. Census Bureau.
• Shuliang Wang, Wenzhong Shi, Hanning Yuan, and Guoqing Chen. 2005. "Attribute Uncertainty in GIS Data". Fuzzy Systems and Knowledge Discvery Conference. 3614, 614-623. https://doi.org/10.1007/11540007_76
• Ningchuan Xiao, Catherine A. Calder, and Marc P. Armstrong. 2007. "Assessing the effect of attribute uncertainty on the robustness of choropleth mapclassification." International Journal of Geographical Information Science. 21:2, 121-144. https://doi.org/10.1080/13658810600894307