[ペアワイズ比較による加重の割り当て (Assign Weights by Pairwise Comparison)] ツールでは、入力変数のセットについて、ペアでの比較により相対的加重が計算されます。 すべてのペア間の比較評価が論理的に一貫していることを確認するための診断機能が用意されています。 このツールでは、評価の整合性の向上に役立つ整合比 (CR) が計算されます。 たとえば、変数 A の重要度が変数 B の 2 倍、変数 B の重要度が変数 C の 2 倍、変数 C の重要度が変数 A と等しいものとしてランク付けした場合、そのペアワイズ評価には整合性がありません。 つまり、A > B かつ B > C の場合、C が A と等しくなることはありません。
CR を許容範囲内に維持することで、整合性のないランク付けを防止することができます。 以下は Saaty (2000) に準拠しています:
- CR <= 0.1 の場合、ペアワイズ比較の整合性は許容範囲内にあります。
- CR > 0.1 の場合、整合性を高めるために比較評価を調整する必要があります。
整合比の計算プロセス
CR 計算のステップは次のとおりです。
- 整合度 (CI) が計算されます。
- 変数の数に基づいてランダム整合度 (RI) が求められます。
- CI を RI で割ることで CR が計算されます。
次の比較マトリックスを例として用いて、5 つの変数について CR を計算する方法を示します。
| 変数 | Solar_Gain | Aspect | Elevation | Dist_to_Road | Dist_to_Elect | Weights |
|---|---|---|---|---|---|---|
Solar_Gain | 1 | 3 | 2 | 2 | 0.333 | 0.235 |
Aspect | 0.333 | 1 | 0.5 | 1 | 0.2 | 0.089 |
Elevation | 0.5 | 2 | 1 | 1 | 0.5 | 0.136 |
Dist_to_Road | 0.5 | 1 | 1 | 1 | 5 | 0.247 |
Dist_to_Elect | 3 | 5 | 2 | 0.2 | 1 | 0.294 |
以下で説明する一連の式が計算で使用されています。
CI の計算
CI は次の式を使用して計算されます。

ここで:
- λ (主固有値) は各変数の λi の平均
- n は入力変数の数
各変数の λi の値は次の式を使用して計算されます。
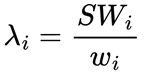
ここで:
- wi は各入力変数について算出された加重を示します (表 1 の加重列)
- SWi は各変数 i の加重合計
各変数の加重合計は次の式を使用して計算されます。

ここで:
- aij は当初のペアワイズ比較マトリックスからの値であり、ここで、i は行、j は列を示します
- wj は対応する変数について算出された加重
たとえば、変数行 Solar_Gain の SW は次のように計算されます。

変数 Solar_Gain の λi は次のように計算されます。
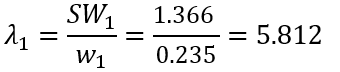
各行についてこれらの計算を繰り返して、各変数の λi の値を求めます。
次に、λi の値の平均を計算して λ を求めます。
この例では、以下の表に示すように、λ は 6.462 です。
| 変数 | 加重(wi) | 加重合計(SWi) | λi = SWi / wi |
|---|---|---|---|
Solar_Gain | 0.235 | 1.366 | 5.812 |
Aspect | 0.089 | 0.541 | 6.079 |
Elevation | 0.136 | 0.826 | 6.070 |
Dist_to_Road | 0.247 | 2.060 | 8.338 |
Dist_to_Elect | 0.294 | 1.765 | 6.005 |
平均 | なし | なし | 6.462 |
λ が計算されたので、上記の式を使用して CI を計算できます。
この例では変数の数が 5 なので、CI の値は次のように計算されます。
CI = (6.462 - 5)/(5 - 1) = 0.365RI の計算
RI は、ペアワイズ比較の CR を計算する際のベンチマークとなる、事前に定義された統計値です。 RI の値は Saaty (2000) によって策定され、マトリックスのサイズごとにモンテ・カルロ シミュレーションから算出されています。 各マトリックス サイズで算出された RI の値を以下の表に示します。 マトリックス サイズは先頭行に示されています。
| マトリックス サイズ | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|
RI | 0 | 0.58 | 0.90 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 |
2 つの変数の比較は本質的に整合しているため、その RI 値は 0 になります。 入力変数の数とともに RI の値が増えます。
この例では、変数の数は 5 なので、その RI 値は 1.12 になります。
CR の計算
CI を RI で割ることで CR が計算されます。 この CR 値は、ペアワイズ比較の整合性の度合いを示します。
この例では、CR は次のように計算されます。
CR = 0.365/1.12 = 0.326CR 値が 0.1 より大きいため、整合性を高めるために比較評価を調整する必要があります。
整合性の向上
入力変数の比較に整合性がないことが明らかになった場合、不整合に最も寄与する 3 つのペアがハイライト表示されます。 ハイライト表示されているペアを調整して、整合性を高める必要があります。
最も整合性がない 3 つのペアを特定するには、以下のワークフローが使用されます。
ペアワイズ比較マトリックスの作成
ペアワイズ整合性評価 (Saaty, 2003) で使用するマトリックスを作成します。 次の式ではこのマトリックスを εij として参照しています。
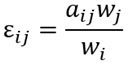
ここで:
- aij は当初のペアワイズ比較マトリックスからの値であり、i は行、j は列を示します。
- wj と wi は j と i について算出された加重です。
値の計算
マトリックスを作成すると、マトリックス εij 内で最も大きい 3 つの値が特定されます。 それらの行と列の変数が、整合性がないペアであると見なされます。
この比較例では、CR 値が 0.1 より大きくなっています (0.326)。 整合性がないペアを特定するため、Solar_Gain 行 Aspect 列のセルの εij の値が次のように計算されます。

すべてのセルについてこの計算を繰り返します。
最も整合性がないペアの特定
上記の比較例のマトリックス εij は次のように作成されます。

マトリックス内の最も大きい 3 つの値は、不整合に最も寄与する比較です。 これらは、変数 Dist_to_Road と Dist_to_Elect の比較評価、変数 Aspect と Dist_to_Road の比較評価、および変数 Dist_to_Elect と Solar_Gain の比較評価です。 この 3 つのペアは、ツール ダイアログ ボックスのスライダーの両側で赤色でハイライト表示されています。
当初の比較マトリックスでは、変数 Solar_Gain は重要度が Dist_to_Road の 2 倍 (Solar_Gain > Dist_to_Road)、Dist_to_Elect の 3 分の 1 (Dist_to_Elect > Solar_Gain) と評価されています。 論理上、Dist_to_Road の重要度は Dist_to_Elect より低くなります (Dist_to_Elect > Dist_to_Road)。 しかし、当初の比較では、Dist_to_Road に Dist_to_Elect の 5 倍の重要度の加重が誤って割り当てられています (Dist_to_Road > Dist_to_Elect)。 これが不整合の主たる原因です。
これを修正するため、スライダーを Dist_to_Elect の側に動かして、CR を再度確認します。 たとえば、Dist_to_Elect 側の 5 までスライダーを動かして [一貫性] ボタンを再びクリックすると、新しい CR は 0.029 になり、比較全体の整合性がとれていることが示されます。

参考文献
Saaty, T. L. 2000. Fundamentals of Decision Making and Priority Theory with the Analytic Hierarchy Process. Pittsburgh, PA: RWS Publications
Saaty, T. L. 2003. "Decision-making with the AHP: Why is the principal eigenvector necessary". European Journal of Operational Research, 145(1), 85-91.