経験ベイズクリギング 3D とは？—ArcGIS Pro

Geostatistical Analyst のライセンスで利用可能。

はじめに

経験ベイズクリギング 3D (EBK3D) は、経験ベイズクリギング (EBK) 手法を使用して 3D のポイントを内挿する地球統計的内挿法です。すべての入力ポイントに、X、Y 座標、高さ、および内挿する計測値が必要です。 EBK3D は、地球統計ウィザード内およびジオプロセシングツールとして利用可能です。

3D 内挿は、次のような場合に適用できます。

海洋学者は、海洋のさまざまな水深の溶存酸素と塩分濃度のマップを作成できます。
大気科学者は、大気中の汚染および温室効果ガスのモデルを作成できます。
地質学者は、鉱物濃度や間隙率などのサブサーフェスの地質特性を推定できます。

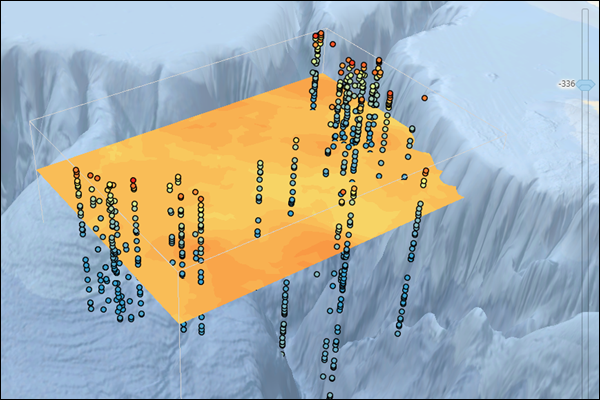
内挿の結果は、指定の標高で水平方向の横断ラインを表示する地球統計レイヤーになります。レンジスライダーを使用して現在の高さを変更すると、レイヤーが更新されて、その新しい高さで内挿された予測が表示されます。任意の高さのラスターおよびフィーチャコンターをエクスポートできるほか、3D のターゲットポイントに推定することもできます。

3D での地球統計レイヤーの視覚化およびエクスポートオプションの詳細

2D および 3D 経験ベイズクリギングの比較

EBK3D の多くの概念と仕組みを理解するには、「経験ベイズクリギングとは？」をご参照ください。サブセット化、セミバリオグラムシミュレーション、混合モデル、および推定のプロセスは、次の例外を除いて同じです。

セミバリオグラムの推定に使用する距離を含むすべての距離は、3D ユークリッド距離を使用して計算されます。
サブセットは 3D で構築されます。
推定に使用する近傍は、3D 検索近傍を使用して求めます。

2D と 3D で同じサブセット化オプション、セミバリオグラムモデル、および変換を使用でき、選択する際の基準も 2D と 3D で同じです。

データ値の水平方向および鉛直方向の変化

3D で収集されたデータの最も困難な特性の 1 つに、ポイントの値が水平方向よりも鉛直方向でより速く変化することが多い点が挙げられます。温度、海水の塩分濃度、気圧などの環境プロセスは、同じ高さに沿って移動しながら、比較的ゆっくりと変化します。ただし、高さの増減に伴って急激に変化します。このため、新しい位置で推定を行うには、鉛直方向よりも水平方向に離れた近傍を探索します。データ値の水平方向と鉛直方向の変化の差異を考慮するには、[高さ拡大係数] を適用し、鉛直方向のリニアトレンドを除去します。

高さ拡大係数

鉛直方向および水平方向の差異を考慮する方法として、まず高さ拡大係数があります。この係数は正の値で、サブセット化およびモデル推定の前に [高さフィールド] 値に乗算されます。高さ値にこの値を乗算することで、水平座標はそのまま、ポイントの高さを鉛直方向にストレッチすることができます。ストレッチした座標で推定を行った後、結果を元の座標に戻してマップに表示します。

ストレッチしたポイントの計測値が、鉛直方向にも水平方向にも同じ割合で変化する拡大係数を選択することが目標です。たとえば、あるポイントの値が水平方向よりも鉛直方向に平均 5 倍速く変化する場合、高さの値に 5 を乗算すると、ポイントの値が鉛直方向と水平方向に同じ速度で変化する新しい座標が生成されます。このように高さ値をストレッチすることで、セミバリオグラムを正確に推定し、検索近傍で適切な近傍を求め、正しい加重を割り当てることができます。

高さ拡大係数が指定されていない場合、実行時に最尤推定を使用して値が推定され、その値がジオプロセシングメッセージとして出力されます。実行時に計算される値は、1 ～ 1000 の値になります。ただし、0.01 ～ 1,000,000 の値を指定できます。計算された値が 1 または 1000 に等しい場合、その範囲外の値を指定して、交差検証に基づく値を選択できます。

注意:

高さフィールドの距離単位が水平座標の単位と異なる場合、高さを水平座標の単位に変換してから高さ拡大係数を計算します。このため、高さフィールドの単位を変更しても、高さ拡大係数の値は変わりません。

鉛直方向のトレンド除去

[トレンド除去の次数] パラメーターを使用すると、鉛直方向のリニアトレンドを除去できます。適用した場合、モデルは Z 座標の一次係数を推定します。このオプションは、高さの増減に伴って体系的に増減するデータに適しています。高さ拡大係数が鉛直方向に急激に変化する値を補正するのに対し、トレンド除去は、値の変化の速さにかかわらず、高さの増減に伴うデータ値の一貫した変化を補正します。このオプションを使用する場合、高さ拡大係数はトレンド除去されたデータ値の観点で解釈する必要があり、通常、トレンド除去が実行されなかった場合よりも小さくなります。

地球統計ウィザードでの 3D 内挿

経験ベイズクリギング 3D は、地球統計ウィザードを使用して対話的な環境で実行できます。入力ポイントの指定、パラメーターの構成、および交差検証結果の表示を、ガイドに従って実行できます。パラメーターの選択、プレビューサーフェスの表示、交差検証結果の調査を行う際の操作性は、2D 経験ベイズクリギングと同じであり、同じチャートおよびオプションがすべて同じ場所に表示されます。

プレビューサーフェスの高さを変更するには、プレビューサーフェスの右側にある高さスライダーをドラッグするか、スライダーの下に値を入力します。これにより、異なる高さの水平横断ラインを対話形式で表示できます。この操作は、ウィザードを使用せずに、レンジスライダーを使用してマップ上の地球統計レイヤーの高さを変更する操作に似ています。また、プレビューページの右下セクションの [Z] 座標に値を入力して、高さを変更することもできます。

[高さ拡大係数] は、デフォルトで自動的に最適化されます。他のパラメーター (セミバリオグラムモデル、サブセットサイズなど) を変更した場合、[最適化] ボタンを使用して新たに最適な高さ拡大係数を計算できます。

パフォーマンスに関する注意事項

このツールのパラメーターを選択する際には、パフォーマンスに関する注意事項があります。次の一部のオプションでは計算時間が長くなるため、許容できる計算時間を維持するには、どの詳細オプションが最も重要かを選択する必要があります。

[高さ拡大係数] パラメーターの推定は、計算時間の大きな部分を占めています。手動で値を入力することで、この計算を回避できます。
変換または K-ベッセルセミバリオグラムモデルを使用すると、推定する必要があるパラメーターが増加し、計算時間が長くなります。
検索近傍の数は、計算時間に影響します。最小近傍数と最大近傍数は近傍の各セクターに適用されるため、たとえば 20 個のセクターを使用し、各セクターで 5 個以上の近傍を使用する場合、各推定で 100 以上の近傍 (20 個の各セクターで 5 個ずつ) が使用されます。大量のセクターを使用する場合、各セクターの近傍数を減らすことをお勧めします。通常、10 ～ 20 個の近傍があれば、正確で安定した推定を行うことができます。

参考文献

Chilès, J-P., and P. Delfiner (1999). Chapter 4 of Geostatistics: Modeling Spatial Uncertainty. New York: John Wiley & Sons, Inc.
Krivoruchko K. (2012). "Empirical Bayesian Kriging," ArcUser Fall 2012.
Krivoruchko K. (2012). "Modeling Contamination Using Empirical Bayesian Kriging," ArcUser Fall 2012.
Krivoruchko K. and Gribov A. (2014). "Pragmatic Bayesian kriging for non-stationary and moderately non-Gaussian data," Mathematics of Planet Earth. Proceedings of the 15^th Annual Conference of the International Association for Mathematical Geosciences, Springer 2014, pp. 61-64.
Krivoruchko K. and Gribov A. (2019). "Evaluation of empirical Bayesian kriging," Spatial Statistics Volume 32. https://doi.org/10.1016/j.spasta.2019.100368.
Pilz, J., and G. Spöck (2007). "Why Do We Need and How Should We Implement Bayesian Kriging Methods," Stochastic Environmental Research and Risk Assessment 22 (5):621–632.