[2 変数空間的関連性 (Bivariate Spatial Association (Lee's L))] ツールは、Lee's L 統計を計算することによって、2 つの連続型解析変数間の空間的関連性 (従属度) を測定します。 この統計は、変数の相関度とその共パターン (空間クラスタリングの類似度) を特徴付けます。 Lee's L 統計の範囲は -1 ~ 1 であり、概念上は相関係数とよく似ていますが、2 つの変数の空間的自己相関を考慮するために調整されています。 Lee's L の値が 1 に近い場合、これらの変数には強い正の相関関係があり (一方が高値である場合、もう一方も高値になる傾向にある)、各変数は強い空間的自己相関を持ちます (変数の高値と低値それぞれが密集する傾向にあります)。 Lee's L の値が -1 に近い場合、これらの変数には強い負の相関関係があり (一方が高値である場合、もう一方は低値になる傾向にある)、各変数は強い空間的自己相関を持ちます。 この値が 0 に近い場合、これらの変数に空間的関連性はありません。つまり、これらの変数には相関関係がないか、空間的自己相関がありません。 この統計を各入力フィーチャにローカルに分割して分類することによって、解析変数の空間的関連性が分析範囲においてどのように変化するかを調べることもできます。
変数に空間的自己相関がある場合はピアソン相関に基づいた従来の統計的検定は有効でないため、解析変数間の空間的関連性を評価する上で変数の空間的自己相関を考慮することが不可欠です。 さらに、これらの従来の検定では、変数間の空間的関係の重要な側面である、2 つの変数間の共パターンは評価されません。
Lee's L 統計は、2 つの解析変数のローカル近傍平均の相関を組み合わせ、各解析変数の空間平滑化スカラーによって相関を調整することによって計算されます。 空間平滑化スカラーの値は 0 ~ 1 の範囲です。 平滑化スカラーが 1 に近い場合は空間的自己相関 (正または負) が強く、この値が 0 に近い場合、値は空間的にランダムで自己相関していません。 空間平滑化スカラーが小さい場合、変数の空間クラスタリングの欠落を調整するため、ピアソン相関と比較して Lee's L 統計が小さくなります。
次の図は、2 つの解析変数のマップとこれらの変数に関連するピアソン相関と Lee's L 統計のさまざまな例を示したものです。 各図で、青色の三角形の値は 1、オレンジ色の三角形の値は 0 になっています。
以下の 1 つ目の図では、両方の解析変数の各位置における値は同じであるため、そのピアソン相関は 1 になります。 さらに、それぞれは強い正の空間的自己相関を持ち、高値と低値それぞれが密集しています。 この結果、Lee's L 統計は 0.801 になり、これは変数間に強い正の空間的関連性があることを示しています。

以下の 2 つ目の図では、2 つ目の解析変数の値が三角形 1 つ分だけ右にシフトして、54 個の三角形のうちの 30 個の値が一致しています。 この結果、ピアソン相関は 0.167 になります。 ただし、各解析変数には強い空間的自己相関があるため、Lee's L 統計はこれより若干高い 0.186 になります。 これは、変数間に弱~中程度の正の空間的関連性があることを示しています。

以下の 3 つ目の図では、2 つ目の解析変数の値が六角形の分析範囲の反対側にシフトして、54 個の三角形のうちの 18 個の値が一致しています。 この結果、ピアソン相関は -0.500、Lee's L 統計は -0.490 になり、これは変数間に中程度~強い負の空間的関連性があることを示しています。

以下の最後の図では、両方の解析変数は負の空間的自己相関を持ち、いずれの三角形も値は同じではありません。 この結果、ピアソン相関は -1、Lee's L 統計は -0.204 になり、これは変数間に弱~中程度の負の空間的関連性があることを示しています。

Lee's L ローカル統計
Lee's L 統計を各入力フィーチャに分割することによって、変数間の空間的関連性が空間的かつローカルにどのように変化するかを調べることができます。 ローカルな相関とローカルな空間平滑化の変化によって Lee's L の全体的な (グローバル) 統計よりも空間的関連性が高くなったり低くなったりする地域や位置が生じることがあります。 Lee's L ローカル統計の値を Lee's L グローバル統計と直接比較することによって、ローカルな空間的関連性がグローバルな空間的関連性より高いか低いかを調べることができます。 グローバル統計とは異なり、ローカル統計は 1 より大きいか -1 より小さいことがあり、ローカル統計の平均は常にグローバル統計と等しくなります。
Lee's L ローカル統計をその統計的有意性と各フィーチャの近傍の値に基づいていくつかのカテゴリに分類することもできます。 各フィーチャには Not Significant、High-High、High-Low、Low-High、Low-Low の 5 つのカテゴリがあります。 あるフィーチャの Lee's L ローカル統計に 90% 以上の統計的有意性がない場合、Not Significant に分類されます。 90% 以上の統計的有意性があり、1 つ目の解析変数の近傍平均が 1 つ目の解析変数の平均より大きく、2 つ目の変数の近傍平均が 2 つ目の変数の平均より大きい場合、High-High として分類されます。 同様に、1 つ目の変数が平均より小さく、2 つ目の変数が平均より大きい場合、Low-High として分類され、1 つ目の変数が平均より大きく、2 つ目の変数が平均より小さい場合、High-Low として分類されます。 2 つの変数に正の空間的関連性がある場合、2 つの変数の低値と高値がそれぞれ密集する傾向にあるため、これらのカテゴリを区別することが重要です。 ただし、どちらの状況でも Lee's L ローカル統計は大きくなるため、両方の変数が高いか両方の変数が低いことで各フィーチャに強い関連性があることがこれらのカテゴリによって明らかになります。 同様に、負の空間的関連性については、1 つ目の変数が高く 2 つ目の変数が低いか 1 つ目の変数が低く 2 つ目の変数が高いことでフィーチャが負の Lee's L ローカル統計を持つかどうかが分類によって明らかになります。
アクティブなマップで実行した場合、この 5 つのカテゴリに基づいて出力フィーチャ レイヤーが描画されます。 正の空間的関連性を持つ変数 (Lee's L グローバル統計が 0 より大きい) 場合、レイヤーには主にカテゴリ High-High と Low-Low が含まれます。 負の空間的関連性を持つ変数 (Lee の L グローバル統計が 0 より小さい) 場合、レイヤーには主にカテゴリ High-Low と Low-High が含まれます。

使用例
このツールは次のようなシナリオで使用できます。
- 大都市のさまざまな地域における教育レベルと世帯収入の間の空間的関連性を調査する。 教育レベルが高い地域と世帯収入の高い地域が一致しているか?
- 植被と大気質の間の空間的関連性を調査する。 植物が多い地域は大気質が良い傾向にあるか? この関連性は統計的に有意であるか?
- 犯罪率と不動産価格の間に関連性はあるか? 大都市圏の地域間で関連性は変化するか?
順列と p 値
順列を使用して、Lee's L グローバル統計とローカル統計の統計的有意性を検定できます。 順列に従って 2 つの解析変数のすべての値が新しい位置にランダムに再割り当てされ (新しい各位置で 2 つの値はペアのまま)、順序が入れ替わった値で Lee's L グローバル統計とローカル統計が計算されます。 このプロセスは何度も繰り返され ([順列の数] の値によって制御)、元の Lee's L グローバル統計およびローカル統計と比較可能な基準分布が構築されます。 元の値が基準分布の端 (右または左) にある場合、元の値がランダムなばらつきの結果である可能性は低く、その空間的関連性は統計的に有意となります。 Lee's L グローバル統計の p 値はジオプロセシング メッセージとして返され、Lee's L ローカル統計の p 値と有意水準は出力フィーチャクラスのフィールドとして返されます。 詳細については、以下の「ツールの出力」のセクションをご参照ください。
注意:
元の値より端にある、順列が入れ替わった値の数に 1 を足したものを、順列の数に 1 を足した数で割った値が p 値になります。 分子と分母に対するこの調整は、小さなサンプル用の調整と、p 値が決して 0 にならないようにするためのものです。 p 値が両側仮説検定からのものとなるように、この値が 2 倍にされます。 検定側は、元の値より端にある値 (元の値より大きい、または小さい、順序が入れ替わった値) がより小さい部分を占める側になります。 Lee's L ローカル統計の p 値は多重仮説検定用には調整されていないため、特定のローカル p 値を解釈する際にはこの点を考慮するようにしてください。
近傍タイプ
空間的関連性を推定するには、Lee's L グローバル統計とローカル統計に各フィーチャの近傍が必要です。 各フィーチャの近傍は [近傍タイプ] パラメーターを使用して指定できます。 このパラメーターには、各フィーチャの近接フィーチャとして使用されるフィーチャを定義する、以下で説明するオプションがあります。 どの近傍タイプでも、フィーチャはそれ自身の近傍に含まれます。
- [固定距離バンド] - 指定した距離内にあるすべてのフィーチャ (最大 1,000 個のフィーチャ) が近接フィーチャとして使用されます。 デフォルトの距離は最短距離であり、各フィーチャに 1 つ以上の追加の近接フィーチャがあることが保証されます。 [距離バンド] パラメーターで距離を指定します。 ポリゴンの場合、重心間の距離を使用して近接フィーチャが特定されます。

- [K 近傍] - フォーカル フィーチャに最も近い一定数のフィーチャが近接フィーチャとして使用されます。 [近傍数] パラメーターで値を指定します。 この値にフィーチャ自体は含まれないため、計算で使用されるフィーチャの数は、指定した値より 1 大きくなります。 ポリゴンの場合、重心間の距離を使用して近接フィーチャが特定されます。

- [隣接エッジのみ] - フィーチャとエッジを共有するポリゴンが近接フィーチャとして使用されます。 この方法はポリゴン フィーチャの場合のみ適用できます。

- [隣接エッジ コーナー] - フィーチャとエッジまたはコーナーを共有するポリゴンが近接フィーチャとして使用されます。 この方法はポリゴン フィーチャの場合のみ適用できます。

- [ドロネー三角形分割] - ポイントの凸包にクリップされた、ドロネー三角形分割 (ティーセン ポリゴン) のエッジまたはコーナーを共有するかどうかによって近接フィーチャが決定されます。 この方法はポイント フィーチャの場合のみ適用できます。

- [空間加重をファイルから取得] - [加重マトリックス ファイル] パラメーターで指定した空間加重マトリックス ファイルによって各フィーチャの近接フィーチャと加重が定義されます。 このファイルは [空間加重マトリックスの生成 (Generate Spatial Weights Matrix)] ツールまたは [ネットワーク空間加重の生成 (Generate Network Spatial Weights)] ツールを使用して作成できます。
距離バンド近傍と近接フィーチャ数近傍の場合、フィーチャに近い近接フィーチャほど、距離とともに減少するカーネル関数を使用した加重は大きくなります。 より近くにある近接フィーチャにより大きい加重を適用するには、[ローカル加重方式] パラメーターで [Bisquare] オプションを指定します。
Bisquare カーネルは次の式を使用して加重を定義します。

カーネル関数は、加重が距離とともに減少する速度を制御するバンド幅に依存します。 各カーネルのバンド幅は、[カーネル バンド幅] パラメーターで指定します。 K 近傍法の近傍の場合に、バンド値を指定しなかった場合、各フィーチャの (k+1) 番目の近接フィーチャまでの距離と等しい (適応) バンド幅が使用されます。 距離バンド近傍の場合、[距離バンド] パラメーターと同じ値がカーネル バンド幅のデフォルト値となります。
注意:
空間加重ファイルでフィーチャ自体への加重が割り当てられていない場合でも、すべてのフィーチャのフィーチャ自体への加重として加重 1 が割り当てられます。 さらに、各フィーチャの近傍の加重が合計 1 になるように正規化されます (行の標準化)。
ツールの出力
このツールから返されるさまざまな出力を使用して、2 つの解析変数間の空間的関連性を調べることができます。 結果はジオプロセシング メッセージ、出力フィーチャクラス、および散布図チャートとして返されます。
ジオプロセシング メッセージ
このツールによって返されるジオプロセシング メッセージには、2 つの解析変数間の全体的な空間的関連性に関連する値が含まれています。 次の値がメッセージに表示されます。
- [Lee's L グローバル] - 2 つの解析変数間の Lee's L 統計。 この値の範囲は -1 ~ 1 です。 正の値は正の空間的関連性があることを示し、負の値は負の空間的関連性があることを示します。 この値が 0 に近い場合、これらの変数に空間的関連性はありません。 この統計は、解析変数間の近傍平均の相関と各解析変数の空間的自己相関度を組み合わせたものです。
- [グローバル p 値] - 統計的に有意な空間的関連性についての両側検定の p 値。 小さい p 値は、Lee's L グローバル統計が統計的に有意であり、ランダムなばらつきによるものではないことを示します。 p 値が有意であり (90% の有意水準では 0.1 未満、95% の有意水準では 0.05 未満、99% の有意水準では 0.01 未満)、Lee's L グローバル統計が正である場合、2 つの解析変数間には強い正の空間的関連性があります。 p 値が有意であり、Lee's L グローバル統計が負である場合、解析変数間には強い負の空間的関連性があります。
- [空間平滑化スカラー (解析フィールド 1)] - 1 つ目の解析変数の空間的自己相関度を示す 0 ~ 1 の範囲の値。 1 に近い値は強い正の空間的自己相関があることを示し (高値と低値それぞれが密集する傾向にある)、0 に近い値は強い負の空間的自己相関があることを示します (高値は低値で囲まれ、低値は高値で囲まれる傾向にある)。
- [空間平滑化スカラー (解析フィールド 2)] - 2 つ目の解析変数の空間的自己相関度を示す 0 ~ 1 の範囲の値。
- [ピアソン相関 (未処理)] - 2 つの解析変数間のピアソン相関。 この値は、Lee's L グローバル統計と比較して、変数間の未処理の相関とその空間的関連性の違いを調べる際に役立ちます。
- [ピアソン相関 (近傍平均)] - 2 つの解析変数の近傍加重平均間のピアソン相関。 Lee's L グローバル統計は、この値に空間平滑化スカラーの平方根を掛け合わせた値ともほぼ等しくなります。
Lee's L グローバル統計、グローバル p 値、ピアソン相関 (未処理) もこのツールの派生出力として返されます。
フィーチャクラスとフィールド
出力フィーチャクラスには、Lee's L ローカル統計の結果を示す次のフィールドが含まれます。
- 各入力フィーチャの 2 つの解析変数およびソース ID のフィールドのコピー。
- [ローカル空間的関連性] (LOCAL_L) - 各フィーチャの Lee's L ローカル統計。 0 より大きい値はその位置において解析変数間に正の空間的関連性があることを示し、0 より小さい値は負の空間的関連性があることを示します。
- [(1 つ目の解析変数) の近傍加重平均] (NWA_VAR1) - 各フィーチャの 1 つ目の解析変数の近傍加重平均。 この値は、[近傍タイプ]、[ローカル加重方式]、[カーネル バンド幅] の各パラメーターによって定義される加重を使用した、フィーチャとその近接フィーチャの値の加重平均です。
- [(2 つ目の解析変数) の近傍加重平均] (NWA_VAR2) - 各フィーチャの 2 つ目の解析変数の近傍加重平均。
- [p 値] (P_VALUE) - 各フィーチャの Lee's L ローカル統計の統計的有意性についての両側仮説検定の p 値。
- [有意水準] (SIG_LEVEL) - 各フィーチャの Lee's L ローカル統計の最も高い有意水準。 値は「有意でない」、「90% 有意」、「95% 有意」、「99% 有意」のいずれかになります。
- [ローカル空間的関連性カテゴリ] (ASSOC_CAT) - 各フィーチャのローカル空間的関連性のカテゴリ。 値は Not Significant、High-High、High-Low、Low-High、Low-Low のいずれかになります。 たとえば、Low-High は、そのフィーチャの有意水準が 90% 以上であり、1 つ目の解析変数の近傍加重平均が 1 つ目の解析変数の平均より小さく、2 つ目の解析変数の近傍加重平均が 2 つ目の解析変数の平均より大きいことを意味します。
- [近傍数] (NUM_NBRS) - 各フィーチャの Lee's L グローバル統計とローカル統計の計算に使用された近接フィーチャの数 (そのフィーチャ自体を含む)。
Lee's L の散布図
出力フィーチャ レイヤーには Lee's L の散布図チャートが含まれており、このチャートの x 軸には 1 つ目の解析変数の近傍加重平均、y 軸には 2 つ目の解析変数の近傍加重平均が表示され、データに適合された線形トレンド ラインも表示されます。 各解析変数の平均値には破線の水平線と垂直線も描画されます。 これらの線によって散布図は 4 つの象限に分割され、これらの線を使用して各ポイントがローカル空間的関連性カテゴリに分類されます。 たとえば、左上の象限にある統計的に有意なフィーチャは Low-High (薄い青色) カテゴリに分類されます。
このチャートを使用して、残りのフィーチャの一般的なトレンドから外れている個々のフィーチャを特定することもできます。 たとえば、散布図でトレンド ラインから遠く離れた位置にある個々のポイントを選択し、それらのフィーチャをさらに詳しく調べることができます。 これらのフィーチャがマップ内で密集し、他の手段では検出するのが困難な空間的関連性の局所的パターンが明らかになることがあります。

ベスト プラクティスおよび制限
このツールを使用する場合、以下を考慮してください。
- どちらの解析変数でも外れ値 (他の値よりも非常に大きいまたは小さい値) は結果に大きく影響します。 各解析変数のヒストグラムを作成して外れ値の有無を調べ、いずれかの変数に外れ値が含まれているフィーチャをすべて削除することをお勧めします。 データ エンジニアリングを使用して外れ値を特定することもできます。
- このツールを使用する場合、2 つの解析変数の近傍加重平均間に線形関係があることが前提となります。 Lee's L の散布図チャート内の値が示すパターンが線形でない場合、[フィールドの変換 (Transform Field)] ツールを使用して解析変数に変換を適用して関係を線形化してから、変換後の値を使用してツールを再度実行できます。
- 統計的に有意な p 値 (通常は 0.05 未満) は、2 つの変数間に相互相関があることを必ずしも意味しません。 そうではなく、変数のいずれかまたは両方に強い空間的自己相関があることのみを意味する場合があります。 有意な p 値を解釈するには、各変数の Lee's L グローバル統計、近傍平均間の相関、空間平滑化スカラーの値を評価します。 これらの値すべてを用いることで、統計的有意性が自己相関から生じているのか、相互相関から生じているのか、あるいはその両方から生じているのかを読み取ることができます。 p 値は有意であるが、Lee's L グローバル統計および近傍平均間の相関がほぼ 0 であり、空間平滑化スカラーが 1 に近い場合、これらの変数それぞれに高い自己相関性があるが、相互相関はほとんどない可能性が高くなります。
- 少なくとも 50 個の入力フィーチャを使用し、各フィーチャに少なくとも 8 つの近接フィーチャを含めることをお勧めします。
式
このセクションでは、このツールによって計算されるすべての統計の式について説明します。 導出などの詳細については、以下の参考文献セクションに記載されている論文をご参照ください。
いずれの式でも、x は 1 つ目の解析変数を指し、y は 2 つ目の解析変数を指します。 変数の上のチルド (~) は、近傍値の加重平均であることを示しています。 各近傍の加重は合計が 1 になるように正規化されます。 変数の上のバーは、n 個の入力フィーチャすべての非加重平均であることを示しています。 添字 i は単一の入力フィーチャを示しています。 式内のいずれの総和もすべての入力フィーチャの合計です。
Lee's L グローバル統計は次の式によって計算されます。

Lee's L グローバル統計は、次のように、空間平滑化スカラーの平方根と近傍加重平均間の相関の積ともほぼ等しくなります。
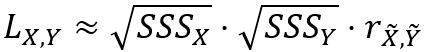
空間平滑化スカラーは次の式によって計算されます。


近傍加重平均間の相関は次の式によって計算されます。
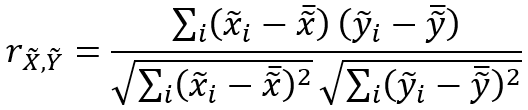
Lee's L ローカル統計は次の式によって計算されます。

次のように、Lee's L グローバル統計は Lee's L ローカル統計の平均と等しくなります。
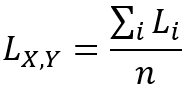
参考文献
このツールの実装には以下の参考文献が用いられています。
- Lee, Sang-Il. "Developing a bivariate spatial association measure: an integration of Pearson's r and Moran's I." Journal of geographical systems 3 (2001): 369-385.「https://doi.org/10.1007/s101090100064」.
- Lee, Sang-Il. "A generalized randomization approach to local measures of spatial association." Geographical Analysis 41.2 (2009): 221-248.「https://doi.org/10.1111/j.1538-4632.2009.00749.x」.