Available with Image Analyst license.
Overview
Estimates the trend for each pixel along a dimension for one or more variables in a multidimensional raster.
Notes
Supported multidimensional raster datasets include Cloud Raster Format (CRF), multidimensional mosaic datasets, or multidimensional raster layers generated by netCDF, GRIB, or HDF format files.
This tool can be used to fit data along a linear, harmonic, or polynomial trend line, or it can be used to perform trend detection using the Mann-Kendall or Seasonal-Kendall test.
The output trend raster generated with this function is used as the input to the Predict Using Trend function.
The Mann-Kendall and Seasonal-Kendall tests are used to determine whether there is a monotonic trend in the data. They are nonparametric, meaning they do not assume a specific distribution of data. The Mann-Kendall test does not consider serial correlation or seasonal effects. If the data is seasonal, the Seasonal-Kendall test is more appropriate.
If the tool is used to perform either the Mann-Kendall or Seasonal-Kendall test, the output is a five-band raster as follows:
- Band 1 = Sen's slope
- Band 2 = p-value
- Band 3 = Mann-Kendall score (S)
- Band 4 = S Variance
- Band 5 = Z-score
The outputs from the Mann-Kendall or Seasonal-Kendall test can be used to determine which pixels in your multidimensional time series have a statistically significant trend. You can use this information in conjunction with the linear, harmonic, or polynomial trend analysis to extract significant trends in your time series. You can generate a mask including pixels with significant p-values, apply the mask to the multidimensional raster, and use this masked multidimensional raster as the input to the tool to perform linear, harmonic, or polynomial trend analysis.
There are three trend line options for fitting a trend to the variable values along a dimension: linear, polynomial, and harmonic. The three trend-fitting options are described below.

For linear trend analysis, the output is a three-band raster as follows:
- Band 1 = Slope
- Band 2 = Intercept
- Band 3 = Root Mean Square Error (RMSE) or the error around the line of best fit
For polynomial trend analysis, the number of bands in the output depends on the polynomial order. Second-order polynomial fitting produces a four-band raster as follows:
- Band 1 = Polynomial_2
- Band 2 = Polynomial_1
- Band 3 = Polynomial_0
- Band 4 = RMSE
Third-order polynomial fitting produces a five-band raster as follows:
- Band 1 = Polynomial_3
- Band 2 = Polynomial_2
- Band 3 = Polynomial_1
- Band 4 = Polynomial_0
- Band 5 = RMSE
For harmonic trend analysis, the number of bands in the output depends on the harmonic frequency. When the frequency is set to 1, the output is a five-band raster as follows:
- Band 1 = Slope
- Band 2 = Intercept
- Band 3 = Harmonic_sin1
- Band 4 = Harmonic_cos1
- Band 5 = RMSE
When the frequency is set to 2, the output is a seven-band raster as follows:
- Band 1 = Slope
- Band 2 = Intercept
- Band 3 = Harmonic_sin1
- Band 4 = Harmonic_cos1
- Band 5 = Harmonic_sin2
- Band 6 = Harmonic_cos2
- Band 7 = RMSE
The Length of Cycle parameter for harmonic trend analysis is used to indicate the number and length of cycles you expect to see in your data throughout a day or year. For example, if you expect your data to go through two cycles of variation in one year, the length of cycle will be 182.5 days or 0.5 years. If you have temperature data collected every three hours, and there is one cycle of variation per day, the length of cycle is one day.
The Frequency parameter for harmonic trend analysis is used to describe the harmonic model to fit to the data. If the frequency is set to 1, a combination of linear and the first order harmonic curve will be used to fit the model. If the frequency is 2, a combination of linear, first order harmonic curve, and second order harmonic curve will be used to fit the data. If the frequency is 3, an additional third order harmonic curve will be used to model the data, and so on.
Model goodness-of-fit statistics can be generated as optional outputs. The root mean-square error (RMSE), R-squared, and the trend slope p-value can be calculated and symbolized. Symbolize the output trend raster layer using the RGB symbology and specify the statistics as the red, green and blue bands.
Parameters
| Parameter | Description |
|---|---|
Raster | The input multidimensional raster. |
Dimension Name | The dimension along which a trend will be extracted for the variable or variables selected in the analysis. |
Trend Type | Specifies the type of line to be used to fit to the pixel values along a dimension.
|
Harmonic Frequency | The frequency number to use in the trend fitting. This parameter specifies the frequency of cycles in a year. The default value is 1, or one harmonic cycle per year. This parameter is only included in the trend analysis for a harmonic regression. |
Length of Cycle | The length of periodic variation to model. The unit is days, regardless of the time unit of the input data. For example, leaf greenness often has one strong cycle of variation in a single year, so the cycle length is 365.25, even if the input data is monthly greenness. Hourly temperature data has one strong cycle of variation throughout a single day, so the cycle length is 1. The default length is 365.25 days for data that varies on an annual cycle. |
Cycle Unit | Specifies the time unit to be used for the length of a harmonic cycle.
|
Polynomial Order | The polynomial order number to use in the trend fitting. This parameter specifies the polynomial order. The default value is 2, or second-order polynomial. This parameter is only included in the trend analysis for a polynomial regression. |
Ignore NoData | Specifies whether NoData values are ignored in the analysis.
|
RMSE | Specifies whether to generate the root mean square error (RMSE) of the trend fit line.
|
R-Squared | Specifies whether to calculate the R-squared goodness-of-fit statistic for the trend fit line.
|
P-value of Slope Coefficient | Specifies whether to calculate the p-value statistic for the slope coefficient of the trend line.
|
Seasonal Period | Specifies the time unit to be used for the length of a seasonal period when performing the Seasonal-Kendall test.
|
Regression types
The regression equation for each trend option is listed below.
- Linear—The linear trend line is a best-fit straight line that is used to estimate simple linear relationships. A linear trend highlights a rate of change that is increasing or decreasing at a steady rate. The formula for the linear trend line is as follows:
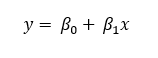
- y = the pixel's variable value.
- x = the dimension value.
- ß0 = the y-intercept.
- ß1 = the linear slope or rate of change.
ß1 > 0 indicates an increasing trend.
ß1 < 0 indicates a decreasing trend.
- Polynomial—The polynomial trend line is a curved line that is useful for data that fluctuates. In this case, a polynomial order value is used to indicate the maximum number of fluctuations that occur. The formula for the polynomial trend line is as follows:
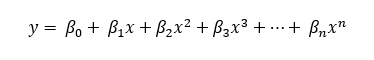
- y = the pixel's variable value
- x = the dimension value
- ß0, ß1, ß2, ß3, ..., ßn = constant coefficients
- Harmonic—The harmonic trend line is a periodically repeating curved line that is best used to describe data that follows a cyclical pattern, such as seasonal temperature changes. The formula for the harmonic trend line is as follows:

- y = the pixel's variable value
- t = the Julian date
- ß0 = the y-intercept
- ß1 = the rate of change
- α, γ = coefficients of inter-annual or intra-annual changes
- ω = i
- f = the harmonic frequency