Как работает инструмент Статистика по блокам

Доступно с лицензией Spatial Analyst.

Инструмент Статистика по блокам выполняет операции, которые вычисляют статистику для входных ячеек в фиксированном наборе не перекрывающихся окон или окрестностей. Статистика (например, максимум, среднее или сумма) вычисляется для всех входных ячеек, содержащихся в каждой окрестности. Результирующее значение для отдельной окрестности или блока присваивается всем ячейкам, попадающим в минимальный ограничивающий прямоугольник, описывающий заданную окрестность.

Обработка окрестности

Концептуально, для каждого блока ячеек алгоритм вычисляет статистику входных ячеек, которые попадают в окрестность заданной формы в блоке. Так как окрестности не перекрываются, любая указанная входная ячейка будет включена в вычисления только для одного блока.

Имеется несколько предустановленных форм окрестности, доступных для выбора. Также можно создать пользовательскую форму. В окрестности можно вычислить следующие статистические параметры: большинство, максимум, среднее, медиана, минимум, меньшинство, диапазон, среднеквадратичное отклонение, сумма и разнообразие.

Инструмент Статистика по блокам работает следующим образом:

• Он создает первую заданную окрестность, например, в форме круга, в верхнем левом углу входного растра или окна анализа.

  

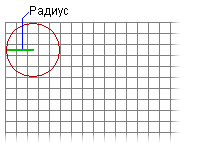
• Вычисляется минимальный ограничивающий прямоугольник с целью определения размера выходного блока.

  

• Он делит оставшуюся область растра на заданные блоки. Блоки не могут перекрываться

  

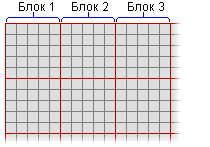
• Инструмент определяет в каждом блоке местоположения ячеек, которые будут использованы в блоковых вычислениях. Местоположения ячеек идентифицируются указанием определенной окрестности — например, круговая окрестность — которая вписана в пределы очерчивающего прямоугольника.

  

• Инструмент вычисляет выходное значение для каждой окрестности каждого блока. Результирующие значения присваиваются местоположению каждой ячейки в соответствующем выходном блоке.

Ячейки NoData

Параметр Игнорировать значение NoData при вычислениях определяет, как в окне окрестности обрабатываются ячейки со значением NoData. Если этот параметр включен (ignore_nodata = "DATA" в Python) любые ячейки NoData в окрестности будут игнорироваться в вычислениях выходного значения для блока. Если этот параметр не отмечен (ignore_nodata = "NODATA" в Python), то при наличии в окрестности ячейки NoData все ячейки выходного блока также будет NoData.

Размер окрестности

Максимальный размер по любому измерению окрестности ограничен 2047 ячейками. Это означает, что прямоугольная окрестность не может быть больше этого числа ячеек по горизонтали или вертикали. Для круглых окрестностей, радиус не может быть больше 1023.

Типы окрестностей

Окрестность может быть в форме кольца, окружности, прямоугольника или клина. Используя керн-файл, вы можете определить пользовательскую форму окрестности, а также присвоить различные веса конкретной ячейке в окрестности до вычисления статистики.

Ниже рассматриваются различные формы окрестности и то, как они определяются:

• Кольцо
  • Форма плоского кольца состоит из двух окружностей, одно внутри другого, формирующих форму бублика. В обрабатываемую окрестность будут включены ячейки, центры которых попадают за пределы круга меньшего радиуса, но внутрь круга большего радиуса. Область между двумя окружностями становится кольцевой окрестностью.
  • Радиус определяется в ячейках или единицах карты и измеряется перпендикулярно оси x или оси y. Если радиусы указаны в единицах карты, то они конвертируются в единицы ячеек. Итоговый радиус в единицах ячеек задаёт область, которая наиболее точно определит область, вычисленную с помощью исходного радиуса в единицах карты. Все ячейки, центры которых попадают между окружностями, будут включены в обрабатываемую окрестность.
  • Окружность кольца по умолчанию – внутренний радиус одной ячейки и внешний радиус трех ячеек.
  • Пример вычисления кольцевой окрестности:

  

  Показаны два обрабатываемых блока с кольцевой окрестностью по умолчанию (внутренний радиус = 1 ячейка, внешний радиус = 3 ячейки).

• Окружность
  • Окрестность в форме круга задаётся значением радиуса.
  • Радиус определяется в единицах ячеек или карты и измеряется перпендикулярно оси x или оси y. Если радиус задан в единицах карты, применяется дополнительная логика, чтобы определить ячейки, задействованные в обрабатываемой окрестности. Сначала рассчитывается точная площадь круга, определенного заданным значением радиуса. Затем определяется площадь для двух дополнительных кругов, причем в одном случае значение заданного радиуса округляется в меньшую сторону, а в другом – в большую сторону. Эти две площади сопоставляются с величиной, полученной для заданного радиуса, и выбирается радиус, для которого получен более близкий результат.
  • По умолчанию радиус окрестности круга равен 3 ячейкам.
  • Пример вычисления окрестности круга:

  

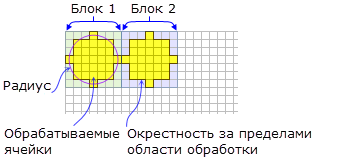
  Показаны два обрабатываемых блока с круговой окрестностью по умолчанию (радиус = 3 ячейки).

• Прямоугольник
  • Окрестность в форме прямоугольника задается путем указания ширины и высоты в ячейках или единицах измерения карты.
  • В обработку окрестности в форме прямоугольника будут включены только те ячейки, чей центр попадает в заданный объект.
  • По умолчанию прямоугольная окрестность является квадратом со стороной, равной трем ячейкам.
  • Пример вычисления прямоугольной окрестности:

  

  Показаны два обрабатываемых блока с прямоугольной окрестностью (ширина = 6 ячеек, высота = 4 ячейки).

• Клин
  • Клин – это окрестность в форме клина, определяемая радиусом, начальным и конечным углами.
  • Клин строится в направлении против часовой стрелки от начального угла до конечного угла. Углы задаются в арифметических градусах от 0 до 360, где 0 находится на положительной x-оси (3:00 часа), и могут быть как целочисленными, так и с плавающей точкой. Могут использоваться отрицательные значения углов.
  • Радиус определяется в ячейках или единицах карты и измеряется перпендикулярно оси x или оси y. Если радиус указан в единицах карты, то они конвертируются в единицы ячеек. Итоговый радиус в единицах ячеек задаёт область, которая наиболее точно представляет область, определенную ранее в единицах карты. Все ячейки, центры которых попадают в клин, будут включены в обрабатываемую окрестность.
  • Клиновидная окрестность по умолчанию имеет углы от 0 до 90 градусов, с радиусом, равным трем ячейкам.
  • Пример вычисления клиновидной окрестности:

  

  Показаны два обрабатываемых блока с клиновидной окрестностью по умолчанию (радиус = 3 ячейки, начальный угол = 0, конечный угол = 270).

• Неправильная
  • Используется для определения окрестности неправильной формы.
  • То, какие ячейки будут включены в окрестность, определяет керн-файл для окрестности неправильной формы.
  • Описанное ниже применяется к керн-файлу для окрестности неправильной формы:
    • Керн-файл для окрестности неправильной формы представляет собой текстовый файл ASCII, который определяет значения и форму окрестности неправильной формы. Файл можно создать с помощью любого текстового редактора. У файла должно быть расширение .txt и не должно быть пробелов в имени.
    • Первая строка задаёт ширину высоту окрестности (количество ячеек в направлении x, затем пробел, затем количество ячеек в направлении y).
    • Последующие строки определяют значение для каждого положения в окрестности, которую они представляют. Пробел между значениями является обязательным.
    • Значение определяет, будет ли положение в окрестности включено в вычисление. Как правило, для идентификации положений, включаемых в вычисления окрестности нерегулярной формы используется значение 1, но можно использовать любое положительное или отрицательное значение, отличное от 0. Значение может быть и с плавающей точкой.
    • Для исключения местоположения в окрестности из вычислений, используйте для соответствующего местоположения в керн-файле значение, равное 0 (но не пустое).

  • Следующий пример показывает содержание нерегулярного керн-файла и окрестности, которую он описывает:

  

  Показано ядро нерегулярной окрестности с иллюстрацией ячеек, используемых в обработке для двух обрабатываемых блоков.

• Вес
  • Так же как и с нерегулярной окрестностью, взвешенная окрестность позволяет задавать окрестности неправильной формы, но также позволяет применять к входным значениям веса.
  • Керн-файл весов задает, какие ячейки будут включены в окрестность, а также веса, на которые будут умножены значения ячеек.
  • Взвешенная окрестность может использоваться только для статистики: среднее, Среднеквадратическое отклонение и сумма.
  • Для файла ядра к взвешенной окрестности применяется следующее:
    • Керн-файл для окрестности типа Вес представляет собой текстовой ASCII-файл формата, который определяет значения и форму окрестности "Вес". Файл можно создать с помощью любого текстового редактора. У файла должно быть расширение .txt и не должно быть пробелов в имени.
    • Первая строка задаёт ширину высоту окрестности (количество ячеек в направлении x, затем пробел, затем количество ячеек в направлении y).
    • Последующие строки определяют значение для каждого положения в окрестности, которую они представляют. Пробел между значениями является обязательным.
    • Для суммарной статистики вес указываться как положительное или отрицательное целочисленное значение или значение с плавающей точкой.
    • Для статистик - среднее и среднеквадратическое отклонение - вес указываться как любое положительное целочисленное значение или значение с плавающей точкой. Отрицательные значения не допустимы для этих типов статистики, поэтому любое положение с отрицательным весом будет игнорироваться в вычислениях.
    • Для исключения местоположения в окрестности из вычислений, используйте для соответствующего местоположения в керн-файле значение, равное 0 (но не пустое).

  • Следующий пример показывает содержание керн-файла весов и окрестности, которую он описывает:

  

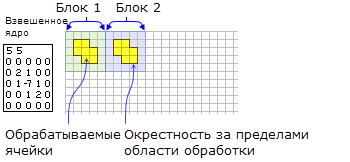
  Показано взвешенное ядро окрестности с иллюстрацией ячеек, используемых в обработке для двух блоков.

Тип статистики

Доступна статистика: Большинство, Максимум, Среднее, Медиана, Минимум, Меньшинство, Диапазон, Стандартное (среднеквадратическое) отклонение (STD), Сумма и Разнообразие. Тип статистики, используемый по умолчанию – Среднее.

Определенные типы статистики доступны только для входных растров целочисленного типа.

• Большинство
  • Входными данными могут быть только целочисленные растры.
  • Определяется частота каждого уникального значения ячейки в блоке окрестности. Если имеется одно значение с максимальной частотой (встречается наиболее часто), это значение присваивается всем ячейкам в этой окрестности. Если имеется связь, присваивается минимальное из связанных значений.
• Максимум
  • Если входной растр целочисленный, значения на выходном растре будут целочисленными; если значения на входном растре представлены числами с плавающей точкой, значения на выходном растре будут также представлены числами с плавающей точкой.
• Среднее
  • Это может быть целочисленный растр или растр с плавающей точкой.
  • Выходной растр всегда будет представлен числами с плавающей точкой.
  • Для типа Взвешенная окрестность это один из поддерживаемых поднаборов типов статистики. См. раздел Взвешенная окрестность для подробной информации о том, как вычисляется статистика.
• Медиана
  • Входными данными могут быть только целочисленные растры.
  • Когда количество действительных значений ячеек в окрестности нечетное, значение медианы вычисляется путем ранжирования значений и выбора среднего значения. Если число значений в окрестности четное, значения будут ранжированы и из двух серединных значений будет выбрано минимальное.
• Минимум
  • Если входной растр целочисленный, значения на выходном растре будут целочисленными; если значения на входном растре представлены числами с плавающей точкой, значения на выходном растре будут также представлены числами с плавающей точкой.
• Меньшинство
  • Входными данными могут быть только целочисленные растры.
  • Определяется частота каждого уникального значения ячейки в блоке окрестности. Если имеется одно значение с минимальной частотой (встречается наименее часто), это значение присваивается всем ячейкам в этой окрестности. Если имеется связь, присваивается минимальное из связанных значений.
• Диапазон
  • Если входной растр целочисленный, значения на выходном растре будут целочисленными; если значения на входном растре представлены числами с плавающей точкой, значения на выходном растре будут также представлены числами с плавающей точкой.
  • Значения для местоположения каждой ячейки на выходном растре определяются по принципу "ячейка-за-ячейкой" путём применения простой формулы: Block Range = Block Maximum – Block Minimum
• Среднеквадратическое отклонение
  • Выходной растр всегда будет представлен числами с плавающей точкой.
  • Для типа Взвешенная окрестность это один из поддерживаемых поднаборов типов статистики. См. раздел Взвешенная окрестность для подробной информации о том, как вычисляется статистика.
  • Среднеквадратическое отклонение вычислено для всей популяции (метод N), а не для выборки (метод N-1).
• Сумма
  • Если входной растр целочисленный, значения на выходном растре будут целочисленными; если значения на входном растре представлены числами с плавающей точкой, значения на выходном растре будут также представлены числами с плавающей точкой.
  • Для типа Взвешенная окрестность это один из поддерживаемых поднаборов типов статистики. См. раздел Взвешенная окрестность для подробной информации о том, как вычисляется статистика.
• Разнообразие
  • Входными данными могут быть только целочисленные растры.

Вычисление взвешенной окрестности

Степень влияния каждого значения окрестности на итоговый результат обрабатываемого блока может настраиваться с помощью весов.

В следующих разделах показаны формулы, используемые для вычисления взвешенного среднего, стандартного отклонения и суммарной статистики. К каждому случаю приводится пример, где показано вычисление обрабатываемого блока с прямоугольной окрестностью 3 х 3.

Статистика Взвешенное среднее

Для взвешенной окрестности со статистикой Среднее выходное значение для ячеек в обрабатываемом блоке является суммой значений весов ядра, умноженной на входное значение, деленное на сумму значений весов ядра.

Формула применяется к ячейкам, находящихся в пределах окрестности, как описано ниже:

Где:

• µ_W взвешенное среднее значение совокупности для обрабатываемого блока.
• N – число ячеек в окрестности.
• w_i – значение веса, определенное для ядра.
• x_i – входное значение ячейки.

Прежние версии:

В предыдущих версиях, в вычислениях использовалось число ячеек как знаменатель.

Значения весов должны быть положительными, и могут быть как целочисленными, так и с плавающей точкой.

Пример

Допустим, у нас блок размером 3 x 3 входных ячейки:

4 6 7 6 7 8 4 5 6

Математическое среднее (сумма / количество) для этих значений: 53 / 9 = 5.889.

Допустим, у нас взвешенное ядро ячеек 3 x 3:

3 3 0.0 0.5 0.0 0.5 2.0 0.5 0.0 0.5 0.0

Это ядро дает максимальную степень влияния на центральную ячейку блока (вес 2), уменьшая влияние четырех диагональных соседних ячеек на центральную (вес 0.5), и делает четыре угловые ячейки не оказывающими влияния (вес 0).

Применение уравнения взвешенного среднего, показанного выше, позволяет получить итоговое значение следующим способом:

= (w1x1 + w2x2 + w3x3 + w4x4 + w5x5 + w6x6 + w7x7 + w8x8 + w9x9) / (w1 + w2 + w3 + w4 + w5 + w6 + w7 + w8 + w9) = ((0*4)+(0.5*6)+(0*7)+(0.5*6)+(2.0*7)+(0.5*8)+(0*4)+(0.5*5)+(0*6)) / (0 + 0.5 + 0 + 0.5 + 2.0 + 0.5 + 0 + 0.5 + 0) = (0 + 3.0 + 0 + 3.0 + 14.0 + 4.0 + 0 + 2.5 + 0) / (0.5 + 0.5 + 2.0 + 0.5 + 0.5) = (3.0 + 3.0 + 14.0 + 4.0 + 2.5) / 4.0 = 26.5 / 4.0 = 6.625

Для сравнения, обычное среднее для девяти входных ячеек равно 5.889. Если в ядро включено только 5 входных ячеек (для которых значение веса не равно 0), но значения весов не рассматриваются, среднее будет равно 6.4 (где 6 + 6 + 7 + 8 + 5 = 32, разделенное на 5).

Статистика Взвешенное стандартное отклонение

Для расчета среднеквадратического отклонения для взвешенной окрестности выходное значение для ячеек в обрабатываемом блоке является результатом следующего выражения:

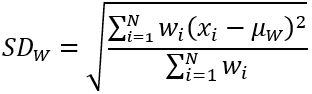
Где:

• SD_W взвешенное значение среднеквадратического отклонения совокупности для обрабатываемого блока.
• µ_W взвешенное среднее значение совокупности для обрабатываемого блока.
• N – число ячеек в окрестности.
• w_i – значение веса, определенное для ядра.
• x_i – входное значение ячейки.

Значения весов должны быть положительными, и могут быть как целочисленными, так и с плавающей точкой.

Если все входные значения окрестности одинаковы, значение среднеквадратического отклонения для всех ячеек в обрабатываемом блоке будет равно 0.

Пример

Значения, использованные в примере взвешенного среднего, снова будут использованы для данного примера.

4 6 7 6 7 8 4 5 6

Также будут использованы такие же значения взвешенного ядра:

3 3 0.0 0.5 0.0 0.5 2.0 0.5 0.0 0.5 0.0

Применение формулы взвешенного среднеквадратического отклонения, приведенного выше для блока ячеек, дает результат примерно 0.85696. Значение записывается в каждую ячейку блока окрестности.

Статистика Взвешенная сумма

Для расчета суммы для взвешенной окрестности выходное значение для ячеек в обрабатываемом блоке является результатом следующего выражения:

Где:

• S_W взвешенное значение суммы совокупности для обрабатываемого блока.
• N – число ячеек в окрестности.
• w_i – значение веса, определенное для ядра.
• x_i – входное значение ячейки.

Значения весов могут быть положительными или отрицательными, как целочисленными, так и с плавающей точкой.

Пример

Рассмотрим следующие входные значения окрестности:

4 6 7 6 7 8 4 5 6

Допустим, у нас взвешенное ядро ячеек 3 x 3:

3 3 -1 -2 -1 0 0 0 1 2 1

Применение показанной выше формулы позволяет получить итоговое значение следующим способом:

= (w1x1 + w2x2 + w3x3 + w4x4 + w5x5 + w6x6 + w7x7 + w8x8 + w9x9) = ((-1*4) + (-2*6) + (-1*7) + (0*6) + (0*7) + (0*8) + (1*4) + (2*5) + (1*6)) = (-4) + (-12) + (-7) + 4 + 10 + 6 = -3

Использование для статистики по блокам

Инструмент Статистика по блокам можно использовать вместо инструмента Изменить разрешение, чтобы понизить разрешение растра. Вместо того, чтобы использовать метод ближайшего соседа, билинейной интерполяции или кубической свертки, иногда лучше присвоить ячейкам растра с более грубым разрешением максимальное, минимальное или среднее значение в рамках нового географического экстента, который включает более крупные ячейки. Для этого, соответствующая статистика применяется к блоку, например, среднее, или максимум.

Инструмент Агрегирование группы Генерализация похож на инструмент Статистика по блокам в том, что он позволяет выполнить агрегирование местоположений ячеек на основании суммы, среднего, медианы, минимального или максимального значения в пространственном окне, которое определяется необходимым выходным разрешением. Однако, между двумя опциями существует два основных различия:

• Выходной растр, полученный в результате выполнения инструмента Агрегирование, пересчитывается в растр с требуемым разрешением.
• В инструменте Агрегирование нет концепции заданной окрестности. Окрестность и выходной блок совпадают, они всегда представлены прямоугольниками и охватывают местоположение одних и тех же ячеек. Размер блока в инструменте Агрегирование определяется путем агрегирования ячеек, необходимого для достижения требуемого разрешения.