Инструмент Оценка чувствительности атрибута неопределенности оценивает, как меняются результаты анализа выбранных инструментов набора Пространственная статистика, когда значения одной или нескольких переменных анализа (атрибутов) являются неопределенными. Неопределенность атрибута может быть задана с помощью пределов погрешности, верхних и нижних границ или заданного процента от исходного значения. Этот инструмент использует выходные данные следующих инструментов:
- Анализ горячих точек
- Оптимизированный анализ горячих точек
- Анализ кластеров и выбросов (Anselin Локальный индекс Морана I)
- Оптимизированный анализ выбросов
- Обобщенная линейная регрессия
- Пространственная автокорреляция (Глобальный индекс Морана I)
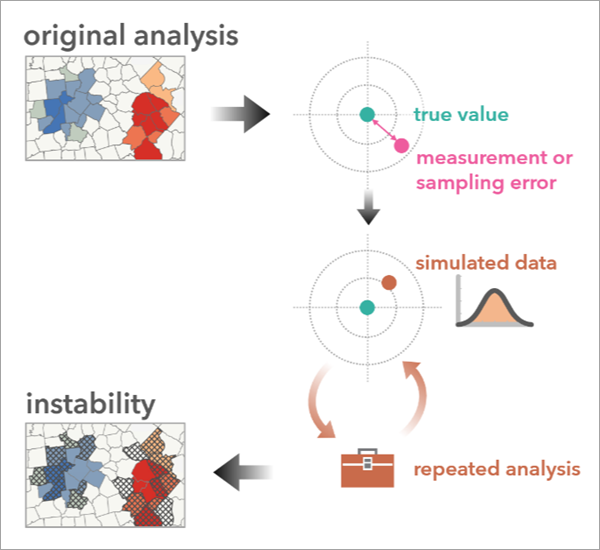
Инструмент выполняет анализ чувствительности путем повторяющегося имитирования новых данных на основе исходной переменной анализа и ее меры неопределенности. Затем он повторно запускает исходный инструмент анализа, используя имитированные данные, и суммирует результаты. Если результаты имитации близки к исходным, вы можете быть уверены в надежности исходных результатов. Однако если результаты с имитированными данными сильно отличаются от исходных, вам следует осторожно подходить к выводам на основе исходных результатов.
Возможное применение
Возможные применения этого инструмента включают следующие варианты:
- Местная благотворительная организация использует анализ горячих точек для определения приоритетности районов в округе для служб по сокращению бедности. Они планируют сосредоточиться на регионах, где анализ показывает высокую степень кластеризации и интенсивности бедности (горячие точки с 99% достоверностью). Отслеживание изменения местоположений горячих точек с течением времени может дать основания для усиления или пересмотра приоритетов обслуживания.
- Крупная розничная сеть разработала модель обобщенной линейной регрессии для оценки того, как демографические факторы, такие как возраст и располагаемый доход, влияют на продажи спортивных товаров. Описательные переменные, собранные в ходе опросов, включают как верхние, так и нижние границы. Учитывая неопределенность в этих переменных, магазин может изучить потенциальный диапазон объемов продаж.
Неопределенность атрибута
Неопределенность атрибута - это вариабельность значений данных, которая обусловлена естественными и неизбежными аспектами сбора и агрегирования данных, такими как ошибка выборки или измерения. Ошибки выборки возникают, когда данные собираются из поднабора популяции, что ставит вопрос о том, насколько хорошо выборка представляет всю популяцию. Ошибка измерения возникает, когда инструмент сбора данных, такой как термометр или анемометр, вносит незначительные изменения в записываемые значения по сравнению с истинными значениями. Данные часто предоставляются с наилучшей оценкой истинного значения измерения, называемой точечной оценкой, и некоторой мерой ее уровня неопределенности. Хотя эти источники неопределенности могут повлиять на точность данных, они присутствуют в любом реальном процессе сбора данных. Распознавание и изучение неопределенности атрибутов и ее влияния на результаты анализа может помочь сделать анализ более прозрачным и надежным.
Как количественно определяется неопределенность
Этот инструмент поддерживает три способа задания неопределенности атрибута: пределы погрешности, верхняя и нижняя границы и процент значений выше и ниже значения атрибута.
Предел погрешности
Предел погрешности представляет собой диапазон, в пределах которого, вероятно, будет находиться истинное значение атрибута. Он связан с уровнем достоверности (например, 90 процентов), указывающим, насколько вы можете быть уверены в том, что фактическое значение атрибута находится в пределах диапазона, определенного оценкой, плюс или минус допустимая погрешность. Например, по результатам опроса может быть установлено, что в округе 2500 человек находятся за чертой бедности, с погрешностью в 300 человек при 90-процентном доверительном уровне. Это означает, что мы можем быть на 90 процентов уверены в том, что истинное число людей за чертой бедности составляет от 2200 до 2800 человек. При использовании этого метода требуется указать поле предела погрешности по крайней мере для одной переменной анализа. Это поле содержит числовую границу погрешности, представляющую, насколько выше или ниже оценки выборки ожидается падение истинного значения популяции. Уровень достоверности по умолчанию равен 90 процентам и может быть скорректирован с помощью параметра Доверительный уровень предела погрешности.

Примечание:
Пределы погрешности обычно записываются в виде полей рядом с исходной переменной. Так обстоит дело со многими переменными в данных ArcGIS Living Atlas of the World, полученных из опросов U.S. Census Bureau’s American Community Survey (ACS). Многие национальные статистические организации предоставляют аналогичные показатели неопределенности.
Верхняя и нижняя границы
Верхняя и нижняя границы представляют неопределенность атрибута путем явного указания диапазона вокруг оценки. В отличие от предела погрешности, верхняя и нижняя границы не обязательно должны быть симметричными относительно точечной оценки.

Процент ниже и выше
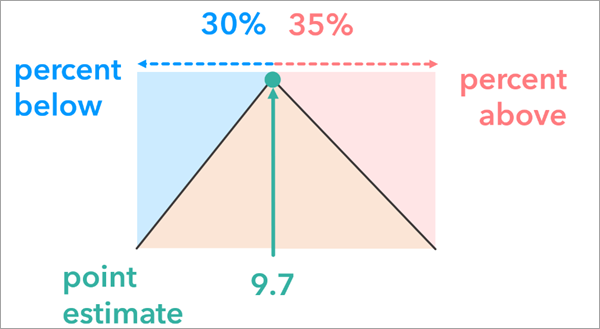
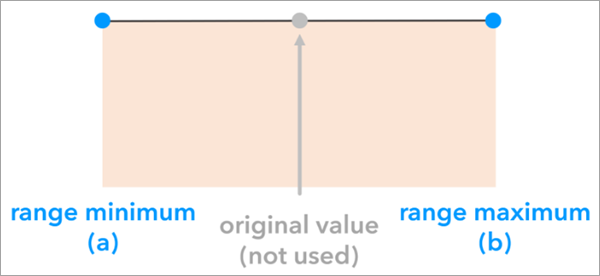
Опция процента ниже и выше отражает неопределенность атрибута путем корректировки исходного значения атрибута каждого объекта на указанный процент. Это создает диапазон оценки, который, вероятно, будет содержать истинное значение. Этот подход может быть полезен, когда другие методы, такие как определение пределов погрешности или верхней и нижней границ, недоступны для выражения неопределенности.
Примечание:
В отличие от параметров предела погрешности и верхней и нижней границ, которые позволяют определять неопределенность атрибута по-разному для каждого объекта, параметр процента ниже и выше применяет одно и то же определение неопределенности для всех объектов.
Использование моделирования для устранения неопределенности
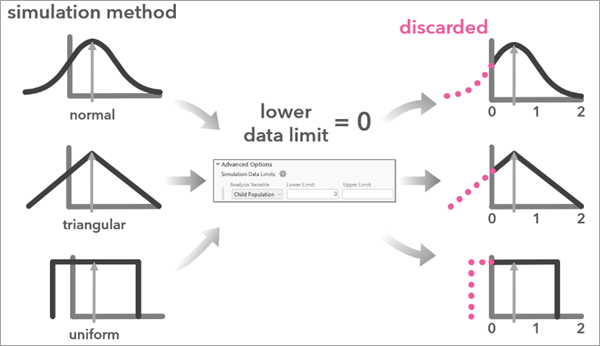
Чтобы оценить, насколько результаты анализа чувствительны к неопределенности, инструмент генерирует смоделированные наборы данных на основе исходной переменной анализа и ее степени неопределенности. В идеале каждый смоделированный набор данных представляет собой правдоподобную версию данных, которые могли бы существовать в реальном мире. Кроме того, существуют различные предположения о том, как истинное значение может быть сосредоточено вокруг точечной оценки или разбросано по ней. Инструмент использует распределения вероятностей для ограничения значений моделируемых данных, чтобы охватить диапазон и вероятность различных реализаций данных. Поддерживаются три вида распределения: нормальное, треугольное и равномерное. Если имитированные данные используются инструментом Обобщенная линейная регрессия, поддерживается корреляция между независимыми переменными. Для анализа с использованием других инструментов, данные имитируются независимо для каждого объекта. Чтобы учесть зависимость между независимыми переменными, их корреляция оценивается глобально, и имитируемые значения для каждого объекта генерируются путем добавления случайного шума многомерного нормального распределения со средним значением, равным нулю, и матрицы ковариации, основанной на глобальной корреляции между независимыми переменными. Поскольку случайный шум основан на многомерном нормальном распределении, имитация для обобщенной линейной регрессии поддерживает только обычный метод имитации.
Нормальное
Опция Нормальное Метода имитации обычно используется, когда доступна допустимая погрешность с соответствующим уровнем достоверности. Эта опция использует нормальное (или гауссово) распределение вероятностей со средним значением, равным значению исходной аналитической переменной, и стандартным отклонением, основанным на величине допустимой ошибки объекта и уровне достоверности.
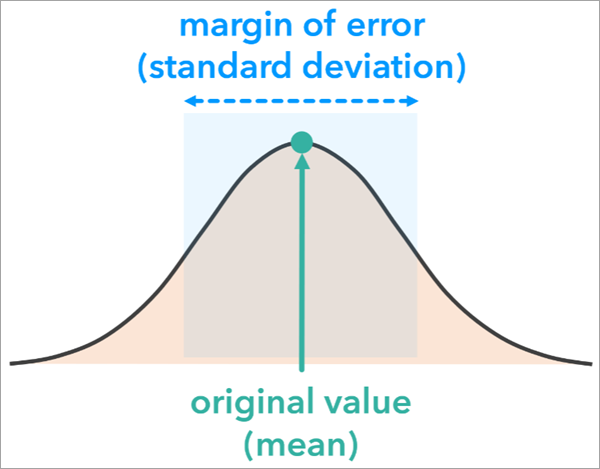
Как следует из формы распределения вероятностей, значения, близкие к первоначальной оценке, будут получены с большей вероятностью, чем значения, расположенные дальше. Однако это может существенно варьироваться в зависимости от предела погрешности. Местоположения с большей погрешностью - часто из-за меньшего размера выборки - будут иметь распределения с более длинными хвостами, что означает, что при моделировании, скорее всего, будут получены значения, более далекие от первоначальной оценки.
Треугольное
Треугольное распределение обычно используется, когда исходное значение представляет собой вероятную оценку истинного значения. Опция Треугольное Метода имитации особенно полезна при асимметричном распределении, когда значения с большей вероятностью сгруппируются вокруг расчетного значения, но с асимметричным разбросом. Треугольное распределение строится и используется для моделирования данных для каждого объекта на основе минимального значения данных, исходного значения объекта и максимального значения данных. Параметр Тип неопределенности определяет минимальное и максимальное значения данных треугольного распределения.
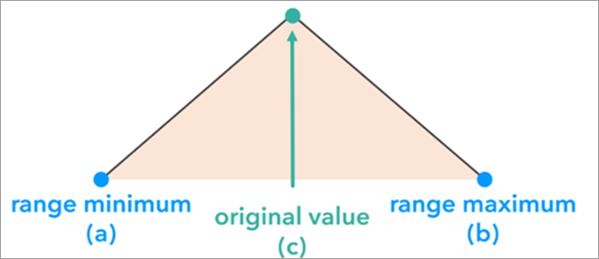
Форма треугольного распределения вероятностей предполагает, что значения, близкие к исходному, будут сгенерированы с большей вероятностью, чем значения, находящиеся в экстремальных точках распределения.
Примечание:
В отличие от нормального распределения, форма не обязательно должна быть симметричной. Например, нижняя и верхняя границы могут отличаться.
Равномерное
Параметр Равномерное Метода имитации используется, когда исходное значение в каждом местоположении является слабой оценкой истинного значения, и единственной доступной информацией о неопределенности атрибута является диапазон возможных значений. Этот параметр использует равномерное распределение вероятности с двумя параметрами: минимальное значение в диапазоне, заданном типом неопределенности, и максимальное значение в диапазоне, заданном типом неопределенности. В отличие от нормального и треугольного распределения, равномерное не использует исходное значение в параметрах распределения вероятностей; каждое значение между минимумом и максимумом с равной вероятностью будет сгенерировано в ходе моделирования.
Поддерживаемые инструменты
В отличие от большинства инструментов геообработки, которые принимают существующий слой в качестве входных данных, входными данными для этого инструмента является итоговый слой следующих инструментов из набора инструментов Пространственная статистика.
- Анализ горячих точек
- Оптимизированный анализ горячих точек
- Анализ кластеров и выбросов (Anselin Локальный индекс Морана I)
- Оптимизированный анализ выбросов
- Обобщенная линейная регрессия
- Пространственная автокорреляция (Глобальный индекс Морана I)
Анализ горячих точек, Оптимизированный анализ горячих точек, Анализ кластеров и выбросов и Оптимизированный анализ выбросов
Для результатов инструментов Анализ горячих точек (Getis-Ord Gi*), Оптимизированный анализ горячих точек, Анализ кластеров и выбросов (Anselin Local Moran’s I) и Оптимизированный анализ выбросов стабильность оценивается путем определения того, как часто объект менял категории при повторных запусках анализа. Например, если объект был горячей точкой с 90-процентной достоверностью в исходном анализе и был переведен в любую другую категорию в одном из прогонов с использованием смоделированных данных, это считается изменением категории. Инструмент подсчитывает, сколько раз менялась категория объекта. Объекты помечаются как нестабильные, если менее 80% результатов моделирования соответствуют исходной категории.
Инструмент создает составной слой, содержащий слой нестабильности и копию исходных результатов анализа.
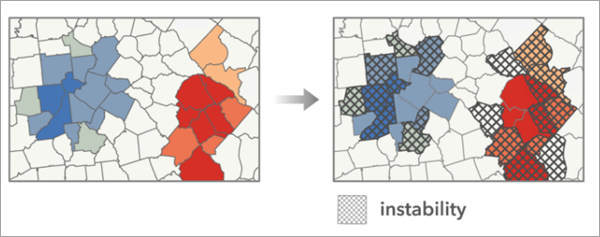
Кроме того, составной слой содержит диаграмму, отображающую количество объектов для каждой исходной категории анализа и каждой преобладающей категории. Преобладающая категория - это та, которая встречалась чаще всего во время всех повторных запусков инструмента в каждом местоположении.
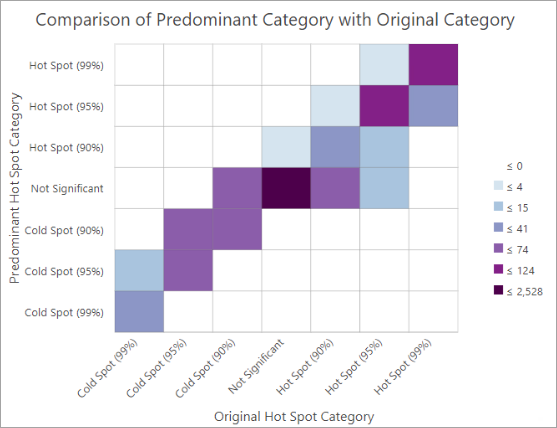
Эта диаграмма может помочь выявить закономерности категорийной нестабильности. Идеально стабильный результат, в котором каждая исходная категория идеально соответствовала бы преобладающей категории, заполняет диагонали ячеек.
Примечание:
Инструмент не поддерживает результаты анализа на основе агрегированных точечных данных, полученных с помощью инструментов Оптимизированный анализ горячих точек и Оптимизированный анализ выбросов.
Инструмент Обобщенная линейная регрессия
При оценке неопределенности анализа Обобщенной линейной регрессии основными результатами этого инструмента являются диаграммы, отображающие распределение диагностических данных регрессии по моделируемым прогонам, такие как R-квадрат и коэффициенты описательных переменных. Инструмент создает составной слой, содержащий копию исходных результатов анализа, таблицу, обобщающую результаты повторных запусков исходного инструмента, и три диаграммы, отображающие распределение R-квадрат, статистическую значимость Харке-Бера и стандартизированные коэффициенты описательных переменных.

Пространственная автокорреляция (Глобальный индекс Морана I)
Что касается результатов анализа инструмента Пространственная автокорреляция (Глобальный индекс Морана I), цель инструмента состоит в том, чтобы понять, насколько достоверной была бы первоначальная оценка глобальной пространственной автокорреляции при неопределенности атрибутов. Инструмент создает составной слой с копией исходных результатов анализа, таблицу, обобщающую результаты повторных запусков инструмента, и диаграммы, отображающие распределение значений индекса Морана и его z-оценки.
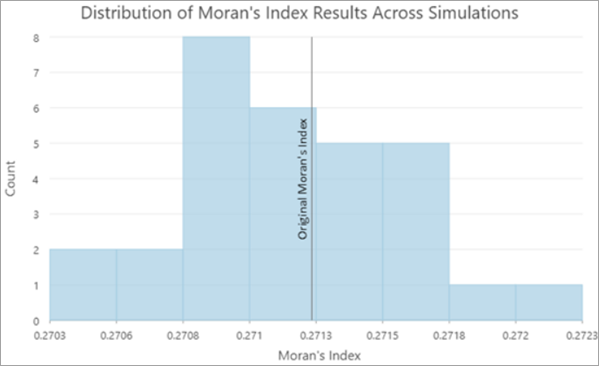
В общем, большинство значений индекса Морана и их z-оценок будет меньше исходных значений, так как добавление случайного некоррелированного шума к значениям данных приводит к снижению пространственной автокорреляции данных.
Примечание:
Пространственная автокорреляция (Глобальный индекс Морана I) не создает выходных объектов. Используйте исходные входные объекты, которые были применены в анализе Пространственной автокорреляции (Глобальный индекс Морана I), в качестве значения Объекты результата анализа.
Дополнительные условия
В подразделе ниже приведены дополнительные сведения.
Изменение порога стабильности в выходных данных
Для результатов инструментов Анализ горячих точек (Getis-Ord Gi*), Оптимизированный анализ горячих точек, Анализ кластеров и выбросов (Anselin Local Moran’s I) и Оптимизированный анализ выбросов слой нестабильности применяет порог стабильности по умолчанию, равный 80 процентам. Это означает, что для того, чтобы объект считался стабильным, он должен быть отнесен к той же категории, что и исходный анализ, более чем в 80 процентах случаев моделирования. Увеличение этого порога приведет к тому, что большее число объектов будет считаться нестабильными, а уменьшение этого порога приведет к тому, что меньшее количество объектов будет считаться нестабильными.
Порог, определяющий стабильность, можно настроить с помощью параметров символов слоя. Чтобы изменить пороговое значение, вы должны сначала найти и выбрать слой нестабильности в выходном составном слое. Откройте панель Символы, затем дважды щелкните значение Верхнее ячейки для класса 80 процентов и измените пороговое значение.

Пределы данных моделирования
Вы можете задать ограничения на диапазон моделируемых значений для анализируемой переменной. Это может быть полезно, когда переменная анализа не должна быть отрицательной (количество) или должна находиться в диапазоне от нуля до 100 (проценты). Используйте параметр Границы данных имитации, чтобы задать диапазон возможных значений для каждой переменной. При задании значения параметра Границы данных имитации инструмент отбрасывает смоделированные значения, которые выходят за пределы указанного диапазона, и повторяет моделирование.
Сохранение промежуточных результатов моделирования
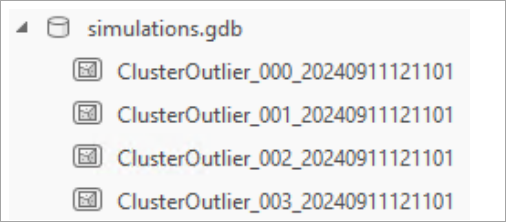
Созданные с помощью этого инструмента модели можно сохранить в виде классов пространственных объектов. Используйте параметр Рабочая область для результатов моделирования, чтобы задать существующую рабочую область, в которой инструмент будет сохранять каждый результат моделирования.
Соглашение об именовании каждого файла имеет следующий формат: Название объекта результатов анализа _ ID моделирования _ Отметка времени моделирования. Каждый класс пространственных объектов, полученных в результате моделирования, содержит схему исходного результата анализа.
Промежуточные результаты моделирования могут быть полезны для дальнейшего анализа. Например, вы можете изучить рабочую область с результатами моделирования Обобщенной линейной регрессии, чтобы лучше понять распределение прогнозируемых значений по результатам моделирования.
Метаданные операций геообработки
Чтобы найти инструмент анализа, входные объекты и дополнительные параметры, используемые в анализе, инструмент считывает метаданные из значения параметра Объекты результата анализа. Соответственно анализ, в результате которого были получены итоговые объекты, должен быть настроен на запись в метаданные.
Этот параметр активирован по умолчанию. Чтобы подтвердить эту установку, откройте диалоговое окно Опции, щелкните вкладку Геообработка и в разделе Журнал убедитесь, что опция Записать операции геообработки в метаданные набора данных включена.

Примечание:
Инструмент не поддерживает анализ Пространственная автокорреляция (Глобальный индекс Морана I), выполняемый на размещенных слоях, поскольку метаданные в этих наборах данных не могут быть изменены.
Дополнительные ресурсы
Для получения более подробной информации обратитесь к следующим ресурсам:
- JingXiong Zhang and Michael Goodchild. 2002. "Неопределенность в географической информации". Taylor & Francis. ISBN 0-203-47132-6. https://doi.org/10.1201/b12624.
- Raphaella Diniz, Pedro O.S. Vaz-de-Melo, Renato Assunção. 2024. “Увеличение объема данных для пространственного картирования заболеваний”. Краткий доклад на симпозиуме по науке о пространственных данных 2021 года. https://doi.org/10.25436/E2KS35
- Michele Crosetto and Stefano Tarantola. 2001. "Анализ неопределенности и чувствительности: инструменты для внедрения моделей на основе ГИС". International Journal of Geographical Information Science. 15:5, 415-437. https://doi.org/10.1080/13658810110053125
- Zhou Dimin. 2010. “Исследование распространения неопределенности атрибутов в ГИС”. Международная конференция 2010 года по интеллектуальным вычислительным технологиям и автоматизации.
- Hyeongmo Koo, Takuya Iwanaga, Barry F.W. Croke, Anthony J. Jakeman, Jing Yang, Hsiao-Hsuan Wang, Xifu Sun, Guonian Lü, Xin Li, Tianxiang Yue, Wenping Yuan, Xintao Liu, and Min Chen. 2020. “Аналитический документ: Анализ чувствительности пространственно распределенных моделей окружающей среды - практическая основа для изучения источников неопределенности”. Environmental Modelling and Software. https://doi.org/10.1016/j.envsoft.2020.104857
- Hyeongmo Koo , Yongwan Chun, and Daniel A. Griffith. 2018. “Геовизуализация атрибутивной неопределенности интервальных и относительных переменных: структура и реализация для векторных данных”. Journal of Visual Languages and Computing 44 89-96. https://doi.org/10.1016/j.jvlc.2017.11.007
- Robert Haining, Daniel A. Grifith, and Robert Bennett. 1983. “Моделирование двумерных автокоррелированных поверхностей”. Geographical Analysis. https://doi.org/10.1111/j.1538-4632.1983.tb00785.x
- Sirius Fuller and Charles Gamble. 2020. "Вычисляем пределы погрешности по методу ACS". Программы и опросы American Community Survey (ACS), Бюро переписи населения США.
- Shuliang Wang, Wenzhong Shi, Hanning Yuan, and Guoqing Chen. 2005. "Неопределенность атрибутов в данных ГИС". Конференция по нечетким системам и обнаружению знаний. 3614, 614-623. https://doi.org/10.1007/11540007_76
- Ningchuan Xiao, Catherine A. Calder, and Marc P. Armstrong. 2007. "Оценка влияния неопределенности атрибутов на надежность картографической классификации хороплет". International Journal of Geographical Information Science. 21:2, 121-144. https://doi.org/10.1080/13658810600894307
Связанные разделы
- Как работает инструмент Анализ горячих точек
- Как работает Анализ кластеров и выбросов (выбросов) (Anselin Локальный индекс Морана I)
- Как работает Оптимизированный анализ горячих точек
- Как работает инструмент Оптимизированный анализ выбросов
- Как работает инструмент Обобщенная линейная регрессия (GLR)
- Как работает Пространственная автокорреляция (Глобальный индекс Морана I)