Инструмент Присвоение весов с помощью попарного сравнения вычисляет относительные веса для набора входных переменных, сравнивая их в парах. Для обеспечения логической согласованности оценок сравнения между всеми парами предоставлена функциональность диагностики. Инструмент вычисляет Коэффициент согласованности (CR), чтобы помочь улучшить согласованность ваших оценок. Например, ваши парные оценки будут несогласованными, если вы оцените значимость переменной A в два раза выше, чем переменной B, значимость переменной B - в два раза выше, чем переменной C, а значимость переменной C будет такой же, как переменной A. То есть, если A > B и B > C, то C не может быть равно A.
Поддержание CR в допустимых границах поможет предотвратить несогласованное ранжирование. В соответствии с Саати (2000):
- Если CR <= 0.1, согласованность для попарного сравнения приемлемая.
- Если CR > 0.1, оценки сравнения необходимо уточнить, чтобы улучшить согласованность.
Процесс вычисления коэффициента согласованности
Шаги вычисления CR включают следующее:
- Вычисляется Индекс согласованности (CI).
- Определяется Произвольный индекс (RI) на основании числа переменных.
- CR вычисляется путем деления CI на RI.
Следующая матрица сравнения будет использоваться в примере, демонстрирующем, как CR вычисляется для пяти переменных.
| Переменная | Solar_Gain | Aspect | Elevation | Dist_to_Road | Dist_to_Elect | Веса |
|---|---|---|---|---|---|---|
Solar_Gain | 1 | 3 | 2 | 2 | 0.333 | 0.235 |
Aspect | 0.333 | 1 | 0.5 | 1 | 0.2 | 0.089 |
Elevation | 0.5 | 2 | 1 | 1 | 0.5 | 0.136 |
Dist_to_Road | 0.5 | 1 | 1 | 1 | 5 | 0.247 |
Dist_to_Elect | 3 | 5 | 2 | 0.2 | 1 | 0.294 |
В вычислениях используется ряд уравнений, описанных ниже.
Вычисление CI
CI вычисляется по следующей формуле:

Где:
- λ (главное собственное число) - это среднее λi для каждой переменной
- n - число входных переменных
Значение λi для каждой переменной вычисляется по следующей формуле:

Где:
- wi обозначает производные веса для каждой входной переменной (Столбец Веса в Таблице 1)
- SWi - взвешенная сумма для каждой переменной i
Взвешенная сумма для каждой переменной вычисляется по следующей формуле:
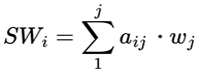
Где:
- aij - значение из исходной матрицы попарного сравнения, где i означает строку, а j - столбец
- wj - производные веса соответствующих переменных
Например, SW для строки переменной Solar_Gain вычисляется следующим образом:

λi для переменной Solar_Gain вычисляется следующим образом:
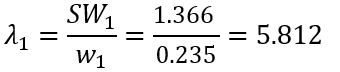
Повторите вычисления для каждой строки, чтобы найти значение λi для каждой переменной.
Затем вычислите среднее значений λi, чтобы получить λ.
В этом примере λ равно 6.462, как указано в таблице ниже.
| Переменная | Веса(wi) | Взвешенная сумма(SWi) | λi = SWi / wi |
|---|---|---|---|
Solar_Gain | 0.235 | 1.366 | 5.812 |
Aspect | 0.089 | 0.541 | 6.079 |
Elevation | 0.136 | 0.826 | 6.070 |
Dist_to_Road | 0.247 | 2.060 | 8.338 |
Dist_to_Elect | 0.294 | 1.765 | 6.005 |
Среднее | Не используется | Не используется | 6.462 |
С вычисленной λ теперь можно рассчитать CI по формуле, приведенной выше.
Поскольку количество переменных в этом примере равно пяти, значение CI вычисляется следующим образом:
CI = (6.462 - 5)/(5 - 1) = 0.365Вычисление RI
RI - это предопределенное статистическое значение, которое служит эталоном для вычисления CR при попарных сравнениях. Разработанные Саати (2000), значения RI получены на основе моделирования методом Монте-Карло для каждого размера матрицы. Полученные значения RI для каждого размера матрицы приведены в таблице ниже. Размеры матрицы указаны в верхней строке.
| Размер матрицы | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|
RI | 0 | 0.58 | 0.90 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 |
Значение RI равно 0 для сравнения двух переменных, так как оно является по своей сути согласованным. Значения RI возрастают с количеством входных переменных.
В этом примере количество переменных равно пяти, поэтому соответствующее значение RI равно 1.12.
Вычисление CR
CR вычисляется путем деления CI на RI. Данное значение CR показывает насколько согласованными являются попарные сравнения.
В этом примере CR вычисляется следующим образом:
CR = 0.365/1.12 = 0.326Поскольку значение CR больше 0.1, необходимо изменить оценки сравнения, чтобы улучшить согласованность.
Улучшение согласованности
Если сравнение входных переменных определяется как несогласованное, выделяются три пары, которые вносят наибольший вклад в несогласованность. Выделенные пары следует настроить, чтобы улучшить согласованность.
Для определения трех наиболее несогласованных пар используется следущий рабочий процесс.
Построение матрицы попарной согласованности
Постройте матрицу, которая будет использоваться в оценке попарной согласованности (Саати, 2003) Эта матрица называется εij в следующей формуле:

Где:
- aij - значение из исходной матрицы попарного сравнения, i указывает строку, а j - столбец.
- wj и wi - производные веса для переменных j и i.
Вычисление значений
После построения матрицы, определяются три наибольших значения εij матрицы. Соответствующие переменные строки и столбца рассматриваются как несогласованные пары.
В данном примере значение CR больше 0.1 (0.326). Для идентификации несогласованных пар значение εij для ячейки строки Solar_Gain и столбца Aspect вычисляется следующим образом:

Повторите вычисления для всех ячеек.
Определение наиболее несогласованных пар
Матрица εij для примера сравнения выше, построена следующим образом:
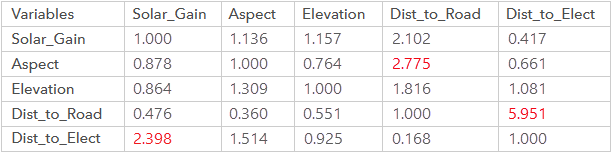
Три самых высоких значения в матрице - это сравнения, которые вносят наибольший вклад в несогласованность. Это оценки сравнения для переменных Dist_to_Road и Dist_to_Elect, для переменных Aspect и Dist_to_Road, и для переменных Dist_to_Elect и Solar_Gain. Эти три пары выделены красным по обе стороны бегунков в диалоговом окне инструмента.
В исходной матрице сравнения переменная Solar_Gain оценивается как в два раза более значимая, чем Dist_to_Road (Solar_Gain > Dist_to_Road), и в три раза менее значимая, чем Dist_to_Elect (Dist_to_Elect > Solar_Gain). Логически Dist_to_Road должна быть менее значимой, чем Dist_to_Elect (Dist_to_Elect > Dist_to_Road). Однако в исходном сравнении при оценке Dist_to_Road был неправильно присвоен вес, в пять раз превышающий значение Dist_to_Elect (Dist_to_Road > Dist_to_Elect). Это является основной причиной несогласованности.
Чтобы исправить это, переместите бегунок в направлении к стороне Dist_to_Elect и просмотрите CR еще раз. Например, если вы переместите бегунок в положение 5 на стороне Dist_to_Elect и нажмите кнопку Согласованность еще раз, новый CR будет равен 0.029, указывая, что общее сравнение теперь согласовано.

Список литературы
Saaty, T. L. 2000. Fundamentals of Decision Making and Priority Theory with the Analytic Hierarchy Process. Pittsburgh, PA: RWS Publications
Saaty, T. L. 2003. "Decision-making with the AHP: Why is the principal eigenvector necessary". European Journal of Operational Research, 145(1), 85-91.