Доступно с лицензией Geostatistical Analyst.
Вариограмма изображает пространственную автокорреляцию измеряемых опорных точек. Как только каждая пара местоположений размещена, через них устанавливается модель. Существуют определенные характеристики, которые обычно используются для описания этих моделей.
Диапазон и порог
Когда вы смотрите на модель вариограммы, на определенном расстоянии, модель выравнивается. Расстояние, на котором модель впервые выравнивается, называется диапазоном. Опорные местоположения, разделённые расстояниями, которые не не превышают диапазон, пространственно автокоррелированы, в то время как местоположения, превышающие диапазон, нет.
Значение, в котором модель вариограммы достигает диапазона (значение на оси y), называется порогом. Частичный порог – это порог минус самородок.
На рисунке ниже показан пример вариограммы:
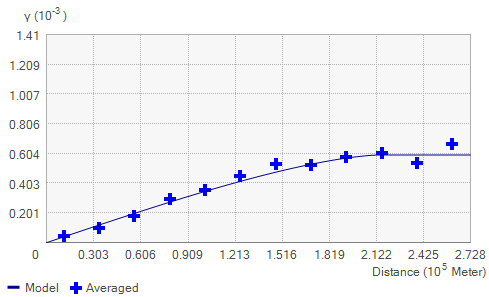
Самородок
Теоретически, на расстоянии нулевого разделения (лаг = 0) значение вариограммы равно 0. Однако на бесконечно малом расстоянии разделения, вариограмма часто изображает эффект самородка, что является значением больше 0. Например, если модель вариограммы пересекает ось y в значении 2, самородок будет равен 2.
Эффект самородка может включать такие атрибуты, как ошибки измерения или пространственные источники изменений на расстояниях, меньших, чем интервал пересчета или оба. Ошибка измерений возникают из-за ошибки измерительного прибора. Естественное явление может изменяться пространственно в диапазоне масштабов. Изменение в микромасштабах, меньших расстояний пересчёта, появится как часть эффекта самородка. До сбора данных важно получить понимание масштабов пространственного изменения.