Многие инструменты и методы в наборе инструментов Пространственная статистика требуют задания пространственных отношений между объектами. Это подразумевает определение того, какие объекты считаются соседними и какое влияние соседи должны оказывать друг на друга. Эта структура, определяемая посредством комбинации типа окрестности и схемы весовых коэффициентов, составляет основу многих типов пространственного анализа.
Пространственные отношения
Важное отличие между пространственной и традиционной статистикой состоит в том, что пространственная статистика интегрирует пространственные отношения непосредственно в вычисления и модели. Поэтому различные инструменты содержат параметр Концептуализация пространственных отношений, Тип окрестности или Пространственные ограничения, который позволяет задавать пространственные отношения между объектами.
Разные пространственные отношения подчеркивают различные аспекты пространственной структуры. Например, при исследовании рынка жилья может иметь смысл определить окрестность каждого дома, как несколько ближайших объектов недвижимости, взвешенных по расстоянию, исходя из предположения, что продажи поблизости оказывают наибольшее влияние. В других ситуациях могут потребоваться более широкие или сложные определения, например, сопоставление городов на основе количества путешествующих между ними людей (когда города, которые географически удалены друг от друга, могут все равно сильно зависеть друг от друга в экономическом плане). Этот выбор влияет на все: от обнаружения пространственных закономерностей до поведения пространственных моделей, поэтому важно подумать о том, какие пространственные отношения лучше всего подходят для ваших данных и вопросов.
При выполнении пространственного статистического анализа, например, анализа горячих точек или анализа кластеров и выбросов, вы можете задать пространственные отношения непосредственно в инструментах, используя параметры инструментов. Однако вы также можете создать файл матрицы пространственных весов (.swm) для хранения соседей и весов, чтобы их можно было повторно использовать в различных инструментах.
Различные инструменты и методы предлагают разные варианты задания пространственных отношений. Хотя ни один инструмент не поддерживает все возможные отношения, инструмент Построить матрицу пространственных весов позволяет создавать широчайший спектр пространственных взаимосвязей, а его выходной файл затем можно снова использовать в других инструментах анализа. Для всех пространственных отношений, за исключением самых простых, рекомендуется сначала задать пространственные отношения в файле матрицы пространственных весов, а затем использовать этот файл в инструментах пространственного анализа.
Различные пространственные отношения, поддерживаемые инструментами, описываются в следующих разделах:
Обратное расстояние

Обратное расстояние в пространстве зависит от импеданса, то есть затухания в зависимости от расстояния, при котором вес соседних объектов уменьшается путем деления на расстояние между соседом и фокусным объектом. Все пространственные объекты воздействуют/влияют на другие пространственные объекты, но, с увеличением расстояния, это влияние снижается. Это обратное расстояние также обычно возводят в степень, например, обратное расстояние в квадрате, что заставляет вес уменьшаться еще быстрее. Обычно рекомендуется использовать с отношениями обратного расстояния пороговое расстояние, чтобы сократить количество соседей с весами, очень близкими к 0. Если указано пороговое расстояние, для вас будет вычислено пороговое значение по умолчанию, но есть возможность принудительного назначения всех объектов соседними по отношению к остальным объектам. Для этого нужно установить значение порогового расстояния, равное 0.
Полоса фиксированных расстояний

Пространственное отношение полосы фиксированных расстояний вводит сферу влияния вокруг каждого объекта, и все объекты в пределах заданного порогового расстояния вокруг фокусного объекта будут включены в качестве соседей. Этот вариант является подходящим, если вы хотите оценить статистические параметры данных при определенном (фиксированном) пространственном масштабе. Если вы изучаете закономерности ежедневных поездок в город из пригородов и знаете, что среднее расстояние поездки составляет 15 миль, вы можете использовать для анализа фиксированное расстояние в 15 миль. Рекомендации по выбору значения диапазона фиксированного расстояния содержат стратегии, которые помогут вам выбрать подходящий для вашего анализа масштаб.
Зона индифферентности

Пространственное отношение Зона индифферентности объединяет полосу фиксированных расстояний и пространственные отношения обратное расстояние. Пространственные объекты, расположенные в пределах диапазона расстояний или порогового расстояния, включаются в анализ целевого пространственного объекта. После достижения порогового расстояния уровень влияния (вес) быстро уменьшается. Этот метод подходит, если вам требуется фиксированный масштаб анализа, но вы не хотите ограничиваться жесткими рамками окрестных объектов, включенных в вычисления для целевого объекта.
Смежность полигонов
Для классов полигональных объектов можно выбрать задание соседей с использованием всех полигонов, смежных с фокусным полигоном. Вы также можете выбрать, следует ли включать в качестве соседей полигоны, у которых есть только общий угол (так называемая смежность ферзя), или только соседей, у которых имеется общее ребро (так называемая смежность ладьи). В различных инструментах эти параметры называются Углы соприкасающихся ребер и Только соприкасающиеся ребра, соответственно. Если какие-то части двух полигонов перекрываются, они будут считаться соседями по обоим параметрам смежности.

Смежность полигонов можно распространить и на более высокие порядки, то есть на большее число шагов, которое необходимо сделать, чтобы перейти от фокусного полигона к его соседям. Смежность первого порядка означает, что соседними будут считаться только непосредственные соседи фокусного полигона (те, до которых можно добраться за один шаг). Второй порядок означает, что все полигоны, до которых можно добраться за один или два шага (соседи первого порядка и все их соседи первого порядка), будут включены в качестве соседей. Если полигоны расположены в виде сетки, более высокие порядки будут образовывать концентрические кольца вокруг фокусного полигона. Обычно рекомендуется избегать использования порядков полигонов, больших 3. С помощью инструмента Построить матрицу пространственных весов можно создавать пространственные отношения смежности более высоких порядков.
K ближайших соседей
Пространственное отношение k ближайших соседей использует заданное число ближайших k объектов в качестве соседей, где k указывается в параметре Количество соседей. В тех местах, где плотность пространственных объектов высока, пространственный масштаб анализа будет меньшим. Соответственно, если плотность объектов невелика, пространственный масштаб анализа будет большим. Преимущество этой модели пространственных отношений состоит в том, что для каждого целевого объекта будет задано некоторое количество окрестностей, даже если плотность пространственных объектов в изучаемой области варьирует в широких пределах.

Триангуляция Делоне
Пространственное отношение Триангуляция Делоне создает окрестности методом построения треугольников Вороного по точечным объектам или по центроидам пространственных объектов, так, чтобы каждая точка/центроид становилась узлом (вершиной) треугольника. Узлы, соединенные ребрами треугольников, рассматриваются как окрестности. Использование триангуляции Делоне позволяет обеспечить для каждого пространственного объекта наличие хотя бы одной окрестности, даже если в данных присутствуют острова или плотность пространственных объектов меняется в широких пределах. Опцию DELAUNAY_TRIANGULATION не следует использовать для наборов данных с совпадающими объектами.

Пространственно-временное окно
С помощью этой опции можно определить отношения объектов как в пространственном (фиксированное расстояние), так и во временном (фиксированный интервал) окне. Эта опция доступна при создании файла матрицы пространственных весов с помощью инструмента Построить матрицу пространственных весов. При выборе опции Пространственно-временное окно требуется указать значения для параметров Поле даты/времени, Тип интервала даты/времени (например, часы, дни или месяцы) и Значение интервала даты/времени. Значение интервала – целое число. Если вы выбрали параметр Часы для типа интервала и 3 для значения этого интервала, то два объекта будут считаться соседними, если значения в их поле Дата/время находятся в пределах трех часов друг от друга. С такой концептуализацией объекты будут соседями, если они расположены на определенном расстоянии и в пределах заданного временного интервала от целевого объекта. В качестве возможного примера, вы могли бы выбрать опцию Пространственно-временное окно для параметра Определение пространственных отношений, если бы хотели создать файл матрицы пространственных весов для его использования в инструменте Анализ горячих точек, чтобы выявить пространственно-временные горячие точки. Дополнительные сведения, в том числе о визуализации результатов, см. в разделе Пространственно-временной анализ. Имеются также другие возможности для визуализации в 3D пространственно-временного куба netCDF.
Получить пространственные веса из файла
Если ваши пространственные отношения заданы в файле матрицы пространственных весов (.swm), используйте эту опцию, чтобы указать файл и применить пользовательские веса к анализу. Эти файлы можно создать с помощью инструмента Построить матрицу пространственных весов, инструмента Построить матрицу пространственных весов для сети, инструмента Проводник окрестности или различных инструментов из группы инструментов Утилиты пространственного компонента (Собственные векторы Морана).
Рекомендации, касающиеся выбора пространственных отношений
Чем более точно вы сможете смоделировать взаимодействие пространственных объектов в пространстве, тем более точные результаты вы получите. Выбор параметра пространственных отношений должен отражать внутренние отношения между пространственными объектами, которые вы анализируете. Иногда на выбор могут влиять характеристики имеющихся данных.
Методы обратного расстояния, например, лучше всего подходят для непрерывных данных или для моделирования процессов, в которых два объекта сближены в пространстве настолько, что с большей вероятностью оказывают влияние друг на друга. При таком пространственном отношении каждый объект является потенциальной окрестностью любого другого объекта, и, при использовании больших наборов данных количество вычислений может стать значительным. Всегда следует пытаться включить пороговое расстояние при использовании отношений обратного расстояния. Это особенно важно для больших наборов данных. Если вы не укажете пороговое расстояние, оно будет вычислено автоматически, но может оказаться не вполне подходящим для вашего анализа. По умолчанию пороговое расстояние равно минимальному расстоянию, которое гарантирует, что для каждого объекта имеется хотя бы одна окрестность.
Метод Полоса фиксированных расстояний хорошо работает с точечными данными и часто с полигональными данными, содержащими полигоны различных размеров (очень большие полигоны по краям изучаемой области и очень маленькие - в ее центре, например), если вам требуется обеспечить согласованный масштаб анализа. Рекомендации по выбору фиксированного значения диапазона расстояний для стратегий помогут вам определить подходящее значение диапазона расстояний для вашего анализа.
Опция Зона индифферентности хорошо работает при правильно подобранном фиксированном расстоянии, но слишком резкие границы отношений окрестностей мешают точному представлению данных. Отношение зоны индифферентности рассматривает каждый пространственный объект как окрестность каждого другого объекта.
Отношения смежных полигонов (варианты Только соприкасающиеся ребра и Углы соприкасающихся ребер) эффективны, когда полигоны имеют одинаковые размеры и однотипное распределение, а пространственные отношения являются функцией близости полигонов (если два полигона имеют общую границу, пространственное взаимодействие между ними возрастает). Если вы выбрали модель смежности полигонов, почти всегда потребуется выбрать нормализацию ряда (значений) для инструментов, которые имеют параметр Нормализация ряда.
Опция K ближайших соседей эффективна, если вам необходимо задать минимальное количество окрестностей для анализа. Если значения, связанные с пространственными объектами, ассиметричны (не имеют нормального распределения), важно, чтобы каждый объект оценивался в контексте как минимум восьми (или около того) окрестностей. Если распределение данных в изучаемом районе неоднородно, т.е., некоторые пространственные объекты расположены очень далеко от всех остальных объектов, этот метод работает очень хорошо. Заметьте, однако, что пространственный контекст анализа меняется в зависимости от изменения плотности используемых пространственных объектов. Если фиксированный масштаб анализа имеет меньшее значение, чем фиксированное число окрестностей, можно использовать метод K ближайших соседей.
Опция Триангуляция Делоне (иногда называемая естественной окрестностью) является хорошим вариантом, если ваши данные содержат островные полигоны (изолированные полигоны, которые не имеют общих границ с другими полигонами), или в тех случаях, когда пространственные объекты распределены слишком неравномерно.
Опция Окно пространства-времени позволяет определить отношения объектов как с точки зрения пространственной, так и временной близости. Этот вариант подходит, например, для выявления горячих точек пространства-времени или построения групп, членство в которых ограничено близостью в пространстве и во времени. Примеры пространственно-временного анализа, а также стратегии для эффективного отображения результатов такого анализа представлены в разделе Пространственно-временной анализ.
Для некоторых приложений пространственные взаимодействия лучше всего моделируются в терминах времени пути или расстояния пути. Если вы моделируете доступность до городских служб, например, или определяете "горячие точки" преступности, рекомендуется выбрать моделирование пространственных отношений в терминах сети. Используйте инструмент Построить матрицу пространственных весов для сети.
Если ни одна из предложенных опций не подходит для вашего анализа, можно создать текстовый ASCII-файл или таблицу, содержащие необходимые вам отношения между пространственными объектами, и затем использовать их для построения файла матрицы пространственных весов. Если один из приведенных выше вариантов близок к желаемому пространственному соотношению, вы можете воспользоваться инструментом Построить матрицу пространственных весов для создания базового файла матрицы пространственных весов и отредактировать свой файл матрицы пространственных весов.
Схемы весов
В то время как пространственные отношения обратного расстояния и зоны индифферентности напрямую применяют веса ко всем соседям на основе расстояния, различные инструменты позволяют вам указать пространственное отношение, сначала определив структуру соседства (например, диапазон расстояний или k ближайших соседей), а затем задав метод применения весов к соседям. Подобно методу обратного взвешенных расстояний, соседям, близким к фокусному объекту, часто присваивают более высокие веса, используя функцию, уменьшающуюся с расстоянием, которую называют ядром. У взвешенного ядра есть преимущество, заключающееся в предоставлении стабильных весов соседям как на близких, так и на дальних расстояниях, тогда как для обратно взвешенного расстояния характерны проблемы на расстояниях, меньших единицы, и веса быстро уменьшаются при удалении от фокусного объекта. Все ядра должны использовать ширину полосы, которая может быть фиксированной или адаптивной и которая определяет, насколько быстро веса будут уменьшаться с расстоянием. Часто используются следующие ядра: биквадратное, Гауссово, триангулярное и квадратическое. Дополнительную информацию о взвешенных ядрах см. в разделе Как работает инструмент Суммарная статистика окрестности.
Инструмент Построить матрицу пространственных весов также позволяет выполнять взвешивание по длине общей границы при задании пространственных отношений с использованием смежности полигонов. Это позволяет вам присвоить большее влияние объектам, у которых общей является большая часть границы фокусных объектов. Вы также можете выполнить взвешивание по значениям поля, например, численности населения или площади полигонов, чтобы присвоить более высокие веса объектам с более высокими значениями поля. При взвешивании по общей границе или значениям в поле все веса будут нормализованы по строке.
Метод расстояния
Некоторые инструменты предоставляют вам выбор между евклидовым или манхэттенским расстоянием.
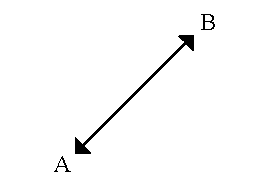
- Евклидово расстояние вычисляется по формуле
D = sq root [(x1–x2)**2.0 + (y1–y2)**2.0]где (x1, y1) – координаты точки A, (x2, y2) – координаты точки B, а D – расстояние по прямой между точками A и B.
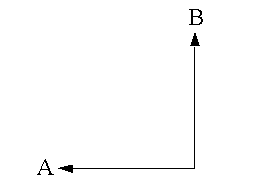
- Манхэттоновское расстояние вычисляется по формуле
D = abs(x1–x2) + abs(y1–y2)где (x1, y1) — координаты точки A, (x2, y2) — координаты точки B, а D — сумма вертикальной и горизонтальной разности между точками A и B. Это расстояние, которое необходимо пройти, если возможность перемещения ограничена только направлениями север-юг и запад-восток. Этот метод дает более точные результаты, чем Евклидово расстояние, если путь ограничен дорожной сетью и если стоимость перемещения по уличной сети не доступна.
Если входные объекты не спроецированы (т.е. координаты указаны в формате широты/долготы) или если для выходной системы координат установлена географическая система координат, расстояния будут вычисляться с использованием измерений по хордам, а параметр Метод расстояний будет отключен. Измерения хордовых расстояний применяются постольку, поскольку они могут быть быстро вычислены и дают точные оценки истинных геодезических расстояний, по крайней мере для точек, расстояние между которыми в пределах порядка тридцати градусов. Хордовые расстояния основаны на сферической модели Земли, и если взять любые две точки на поверхности, хордовое расстояние между ними представляет собой трехмерное расстояние по прямой линии, соединяющей их (эта прямая линия пройдет через Землю). Хордовые расстояния выражаются в метрах.
Внимание:
Рекомендуется производить проецирование своих данных, если изучаемая область распространяется на 30 и более градусов. Хордовые расстояния не обеспечивают точных оценок геодезических расстояний, превышающих 30 градусов.
Самовзвешивание
Несколько инструментов позволяют определять объекты и веса как собственных соседей. Это называется самовзвешиванием. Например, вы можете использовать собственные веса для отражения средних затрат на внутризональные поездки на основе размера полигона. Инструмент Анализ горячих точек позволяет вам выбрать поле, содержащее собственные веса, в параметре Поле собственного потенциала. Инструменты Построить матрицу пространственных весов для сети и Суммарная статистика окрестности позволяют включать собственные веса с помощью параметра Включить фокусный объект. Ряд других инструментов, например, Бивариантная пространственная связь (L-статистика Ли), автоматически добавляют собственные веса ко всем указанным пространственным отношениям.
Нормализация по строке
Нормализация ряда рекомендуется, независимо от того, распределены ли объекты потенциально предвзято в зависимости от дизайна примера или от установленной схемы агрегации. При выборе нормализации по строке каждый вес делится на сумму его строки (сумму весов всех соседних объектов), так что сумма весов будет равна 1. Нормализация по строке часто используется с окрестностями с фиксированным расстоянием и почти всегда применяется для окрестностей, основанных на смежности полигонов. Это для того, чтобы смягчить смещение из-за того, что объекты имеют разное количество соседей. Нормализация по строке вычисляет относительную, а не абсолютную схему весовых коэффициентов, которая подходит, например, при работе с административными границами.
Диапазон расстояний
Параметр Диапазон расстояний (иногда называемый пороговым расстоянием) задает масштаб анализа для большинства пространственных отношений. Выбор подходящего расстояния очень важен. Некоторые пространственные статистические показатели требуют для каждого объекта иметь как минимум одного соседа для того, чтобы анализ был надежный. Если диапазон расстояний слишком мал (настолько, что у некоторых объектов нет соседей), появится соответствующее предупреждение. Инструмент Вычислить диапазон расстояний до числа соседних объектов позволяет оценить минимальное, среднее и максимальное расстояния для указанного количества соседей, и может помочь вам определить подходящий диапазон расстояний для анализа. Дополнительные инструкции см. Рекомендации по выбору диапазона фиксированных расстояний.
Когда значение не указано, рассчитывается пороговое расстояние по умолчанию. В следующей таблице показано, как ведут себя различные пространственные отношения для каждого из трех возможных типов входных данных (отрицательные значения недопустимы):
| Обратное расстояние, обратное расстояние в квадрате | Полоса фиксированных расстояний, Зона индифферентности | Близость полигонов, Триангуляция Делоне, К ближайших соседей | |
|---|---|---|---|
| 0 | Пороговое и предельное значения не применяются; каждый объект – сосед для каждого другого объекта. | Неверно. Будет сгенерирована ошибка выполнения. | Игнорировано |
| пусто | Будет вычислено расстояние по умолчанию. Значение по умолчанию – это минимальное расстояние, которое гарантирует каждому объекту как минимум 1 соседа. | Будет вычислено расстояние по умолчанию. Значение по умолчанию – это минимальное расстояние, которое гарантирует каждому объекту как минимум 1 соседа. | Игнорировано |
| положительное число | Ненулевое, положительное значение будет использовано как предельное расстояние; соседские взаимосвязи будут только существовать среди объектов в пределах этой дистанции. | Для полосы фиксированных расстояний, только объекты в пределах этого указанного предельного расстояния будут соседями. Для зоны индифферентности, объекты в пределах указанного предельного расстояния будут соседями; объекты за пределами этого расстояния тоже будут соседями, но будут иметь все меньший и меньший вес/влияние по мере увеличения расстояния. | Игнорировано |
Число соседей
Параметр Количество соседей служит для различных пространственных отношений. Для отношений K ближайших соседей каждый целевой объект будет использовать ближайшие к нему K объектов (где K — указанное количество соседей). Для отношений Обратного расстояния и Диапазона расстояний пороговое расстояние для объекта будет расширяться, чтобы у него было не менее K объектов. Для пространственных отношений примыкания (смежности) полигонов будут добавлены дополнительные соседи на основе близости центроида объекта, чтобы обеспечить наличие не менее K соседей.
Текстовый файл матрицы весов
Некоторые инструменты позволяют вам задать пространственные отношения среди объектов, указав файл матрицы пространственных весов (.swm). Пространственные веса — это числа от 0 до 1, которые отражают взаимодействие и взаимовлияние между каждым объектом и всеми остальными объектами набора данных. Файл матрицы пространственных весов можно создать с помощью инструмента Построить матрицу пространственных весов или использовать обычный ASCII-файл.
Когда файл матрицы пространственных весов – просто текстовый ASCII-файл, первая строка должна быть именем уникального поля ID. Это позволяет гибко использовать любое числовое поле из набора данных в качестве ID, при генерации файла; однако поле с ID должно быть целочисленным (длинным или коротким) и содержать уникальные значения для каждого объекта. После первой строки файл пространственных весов должен быть отформатирован в следующие 3 колонки:
- От ID объекта
- К ID объекта
- Вес
Например, предположим, что у вас есть 3 АЗС. Поле, которое вы используете в качестве поля ID, называется StationID, а ID объектов – 1, 2 и 3. Вы хотите смоделировать пространственные отношения между этими тремя АЗС, используя обратное время в пути. ASCII-файл может выглядеть следующим образом:

Ввод значений для файла матрицы пространственных весов может оказаться обременительным. Более эффективный способ — использование инструмента Построить матрицу пространственных весов для создания файла матрицы пространственных весов.
Файл матрицы пространственных весов (.swm)
Инструмент Создать матрицу пространственных весов создаст файл матрицы пространственных весов (.swm), определяющий пространственные отношения между всеми объектами в вашем наборе данных на основе заданных вами параметров. Этот файл создается в двоичном формате, чтобы его нельзя было просматривать напрямую. Для просмотра или изменения отношений объектов в файле .swm используйте инструмент Преобразовать матрицу пространственных весов в таблицу.
Вы также можете использовать инструмент Построить матрицу пространственных весов, чтобы преобразовать эту таблицу в файл .swm. В таблице должны содержаться следующие поля:
| Имя поля | Описание |
|---|---|
| <Уникальное имя поля ID> | Целочисленное поле с уникальными значениями для всех объектов. Имя и тип поля должны соответствовать полю уникальных идентификаторов объектов. Например, если у объекта с ID, равным, 6, четыре соседа, значение 6 будет повторено в этом поле четырежды - по одному разу для каждого соседа. |
| NID | Целочисленное поле, содержащее ID соседа. |
| WEIGHT | Числовой вес от 0 до 1, соответствующий взаимовлиянию или взаимодействию между двумя объектами. |
Самый простой способ редактирования файла .swm с пользовательскими весами — создать исходный файл .swm и преобразовать его в таблицу. Эта таблица будет содержать корректные имена и свойства полей, поэтому вы сможете создавать и редактировать строки, чтобы назначать пользовательские соседские отношения и веса. Таблицу также необходимо отсортировать по уникальному идентификатору, а затем по идентификатору соседа.
Публикация файлов матриц пространственных весов
Результатом работы инструмента Построить матрицу пространственных весов является файл .swm. Этот файл привязан к входному классу объектов, полю уникального идентификатора и настройкам выходной системы координат на момент создания файла .swm. Другие люди могут продублировать пространственные отношения, которые вы задаете для анализа, используя ваш файл .swm и тот же входной класс объектов или класс объектов, связывающий все или часть объектов с соответствующим полем Unique ID. Особенно, если вы планируете делиться своими файлами .swm с другими пользователями, избегайте использования выходной системы координат, которая отличается от пространственной привязки исходных объектов. Рекомендуется сначала спроецировать входные объекты и создать файл матрицы пространственных весов для новой пространственной привязки.
Пространственные веса для сети
В некоторых видах анализа пространственные отношения лучше задавать по расстоянию перемещения по сети, а не по непосредственной близости. Например, при моделировании времени реагирования на чрезвычайные ситуации может оказаться более целесообразным задавать соседей на основе кратчайшего времени проезда по дорожной сети, а не по Евклидову расстоянию. Для таких наборов данных можно использовать инструмент Построить матрицу пространственных весов для сети, чтобы задать пространственные отношения с помощью сетевого набора данных сети, определяя пространственные отношения с точки зрения структуры базовой сети.