Когда мы смотрим на мир вокруг нас, мы автоматически организуем, группируем, дифференцируем и классифицируем то, что видим, чтобы лучше понять окружающие нас объекты. Такой тип ментальной классификации необходим для обучения и понимания. Аналогично для лучшего изучения данных можно использовать инструмент Многомерная кластеризация. Используя число создаваемых кластеров, инструмент ищет решение, в котором все объекты в каждом кластере максимально похожи, а сами группы максимально отличаются друг от друга. Сходство объектов основано на наборе атрибутов, указываемых для параметра Поля анализа, а кластеры создаются методом k-средних.
Подсказка:
Кластеризация, группировка и классификация - самые часто используемые методы машинного обучения. Инструмент Многомерная классификация использует методы обработки «без обучения» для нахождения естественных кластеров ваших данных. Эти методы классификации называются классификацией «без обучения», так как не требуют набора классифицированных заранее объектов для «тренировки» алгоритма в целях дальнейшего поиска кластеров в ваших данных.
Хотя существуют сотни алгоритмов кластерного анализа, все из них классифицируются как NP-трудные. Это означает, что единственный способ гарантировать, что решение идеально максимизирует сходства в группе и различия между группами – перепробовать все возможные комбинации объектов, которые требуется сгруппировать. Хотя этого можно добиться при небольшом количестве объектов, задача быстро становится трудноразрешимой.
При этом не только нельзя найти оптимальное решение, но также нельзя определить алгоритм группировки, который будет работать лучше всего для всех возможных типов данных и сценариев. Кластеры бывают разных форм, размеров и плотностей. Атрибуты могут содержать данные с различными диапазонами, симметрией, непрерывностью и единицами измерений. Это объясняет, почему за последние 50 лет было разработано столько разных алгоритмов кластеризации. Эти инструменты следует рассматривать как исследовательский инструмент, позволяющий узнать больше о структурах в ваших данных.
Возможное применение
Некоторые способы использования этого инструмента перечислены ниже:
- Предположим, что у вас есть образцы сальмонеллы из ферм в вашей области. К атрибутам относятся тип/класс, расположение, а также дата и время. Чтобы лучше понять, как бактерии передаются и распространяются, можно использовать инструмент Многомерная кластеризация, чтобы разбить образцы на отдельные "вспышки". Хотя сам по себе анализ не является пространственным, по мере распространения эпидемия вы можете обнаружить в ваших результатах и пространственные закономерности. После определения кластеров можно использовать другие инструменты анализа пространственных шаблонов, такие как Эллипс стандартных отклонений, Усредненный центр или Ближайший объект для анализа каждой вспышки.
- Если вы собрали данные о наблюдении животных, чтобы лучше понять территорию их обитания, то и здесь инструмент Многомерная кластеризация может оказаться полезным. Знания о том, где и когда собираются стаи лосося, например, могут помочь в проектировании защищенных областей для обеспечения успешного нереста.
- Группируя клиентов на основе покупательских предпочтений, демографических характеристик, закономерностей перемещения или других поведенческих атрибутов, можно создать эффективную маркетинговую стратегию для продукции вашей компании.
Входные данные
Инструмент берет точечные, линейные или полигональные Входные объекты, путь к Выходным объектам, одно или несколько Полей анализа и целочисленное значение создаваемого Числа кластеров. Имеется также несколько дополнительных параметров, в том числе Метод инициализации и Выходная таблица оценки оптимального количества кластеров.
Поля анализа
Выберите числовые поля, которые отражают относительные, интервальные или порядковые системы измерений. Хотя номинальные данные могут быть представлены с помощью бинарных переменных, это обычно не работает, как и другие числовые типы переменных. Например, можно создать переменную Rural и назначить каждому объекту (например, каждому смежному кварталу переписи) значение 1, если это сельский объект, или значение 0, если это городской объект. Хороший пример использования этой переменной – это количество или доля площади сельскохозяйственных земель, связанная с каждым объектом.
Примечание:
Значения Полей анализа стандартизированы инструментом, так как переменные с большими диапазонами значений (в которых данные сильно растянуты относительно среднего) будут иметь большее влияние на кластеры, чем переменные с небольшими диапазонами значений. Нормализация значений атрибутов включает z-трансформацию, где средняя величина всех значений вычитается из каждого значения и делится на стандартное отклонение, вычисленное для всех значений. Стандартизация помещает все эти атрибуты на одни весы, даже когда они представлены совершенно разными типами чисел: коэффициентами (от 0 до 1,0), численностью население (значение свыше 1 миллиона) и расстояниями (например, километрами).
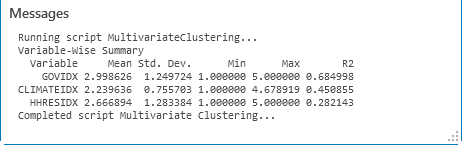
Необходимо выбрать переменные, которые, по вашему мнению, будут отличать один кластер объектов от другого. Предположим, вы хотите сгруппировать школьные округа по успеваемости учеников в стандартных тестах. Вы можете выбрать поля анализа, такие как общие оценки по тестам, результаты для каждого предмета, например математика или литература, процент учеников, получивших минимальную оценку по тесту, и т. д. При запуске вами инструмента Многомерная кластеризация для каждой переменной вычисляется значение R2 и передается в окно сообщений. В сводных данных ниже, школьные округа сгруппированы на основе баллов учеников, набранных при тестировании, процента взрослых, которые не окончили среднюю школу, затрат на каждого ученика и среднего соотношение числа учеников и учителей. Обратите внимание, что у переменной TestScores самое большое значение R2. Это означает, что данная переменная наиболее эффективно разделяет школьные округа на кластеры. Значение R2 отражает, в какой степени вариация в исходных данных TestScores была сохранена в процессе группировки. Чем больше R2 для конкретной переменной, тем лучше переменная различает ваши объекты.
Более подробно:
R2 вычисляется следующим образом:
(TSS – ESS) / TSS
Где TSS – общая сумма квадратов, а ESS – объясненная сумма квадратов. TSS вычисляется за счет возведения в квадрат и суммирования отклонений от глобального среднего значения для переменной. ESS вычисляется одинаково, только отклонения применяются по группам: каждое значение вычитается из среднего значения для группы, которой оно принадлежит, а затем возводится в квадрат и суммируется.
Число кластеров
Иногда вы можете знать наиболее подходящее для ответа на ваш вопрос и проблему и можете ввести значение параметра Число кластеров. Но во многих случаях критерий для выбора точного числа кластеров не доступен. Вместо этого вам нужно получить число, которое лучше всего позволяет классифицировать сходства и различия объектов. В этой ситуации можно установить отметку Число кластеров и позволить инструменту Многомерная кластеризация оценить эффективность деления объектов на 2, 3, 4 и до 30 групп. Эффективность группировки измеряется с помощью псевдо-F-статистики Калински-Харабаза, которая является отношением вариации между кластерами к вариации внутри кластера: Другими словами, то отношение схожести объектов внутри группы к различию объектов между группами:
Метод кластеризации
Инструмент Многомерная кластеризация использует алгоритм K-средних по умолчанию. Цель этого алгоритма – разделить объекты так, чтобы различия между объектами внутри кластера были минимальными для всех кластеров. Так как алгоритм является NP-трудным, для группировки объектов используется «жадная эвристика». «Жадный» алгоритм всегда сводится к локальному минимуму, но не всегда находит глобальный (оптимальный) минимум.
Алгоритм K-средних сначала определяет источники, которые используются для формирования каждого кластера. Соответственно число начальных объектов всегда равно Числу кластеров. Первый начальный объект выбирается произвольно. При выборе оставшихся начальных значений (хотя случайный компонент также используется) применяется взвешивание, которое отдает предпочтение объектам, наиболее отдаленным от существующего набора начальных объектов (эта часть алгоритма называется K-средних ++). Из-за применения случайного компонента при поиске исходных объектов при выборе опции Оптимизированные расположения начальных объектов или Случайные расположения начальных объектов для параметра Метод инициализации могут возникать различные результаты кластеризации при нескольких запусках инструмента.
После определения исходных объектов все объекты назначаются ближайшему исходному объекту (в пространстве данных). Для каждого кластера объектов вычисляется центр данных, а каждый объект назначается ближайшему центру. Процесс вычисления центра данных для каждого кластера и назначения объектов ближайшему центру продолжается до стабилизации кластеров (возможно до 100 итераций).
Подобно алгоритму K-средних К-медоиды определяют исходные объекты, вокруг которых и формируются кластеры. Каждый исходный объект – существующий объект во Входных объектах. Эти исходные объекты называются – медоиды. Все объекты назначаются ближайшему медоиду (ближайшему в пространстве данных). Таким образом выполняется начальная кластеризация. Вычисляется сумма расстояний (в пространстве данных) между медоидами и объектами – не медоидами. Для рамках вычисления внутри каждого кластера медоид меняется местами с каждым объектом – не медоидом, и замет рассчитывается сумма расстояний (в пространстве данных) между каждым медоидом и не медоидом. Если при замене сумма расстояний увеличивается, замена отменяется, в противном случае замененный объект становится новым медоидом. Процесс поиска нового медоида и переназначения объектов ближайшему медоиду выполняется до тех пор, пока участники кластеров не будут определены окончательно.
K-средние и K-медоиды – два алгоритма вычисления кластеризации, которые, в общем, выдают схожие результаты. Но метод К-медоидов более чувствителен к шуму и выбросам у Входных объектов. Алгоритм K-средних, как правило, выполняется быстрее K-медоидов и применяется для больших наборов данных.
Выходные данные
Число выходных объектов, создаваемых инструментом Многомерная кластеризация. Сообщения можно просмотреть на панели Геообработка, поместив курсор на индикатор прогресса, щелкнув кнопку индикатора прогресса инструмента 
, либо развернув раздел сообщений в нижней части панели Геообработка. Вы можете получить доступ к сообщениям для выполненного ранее инструмента Многомерная кластеризация из панели История геообработки.
Результатом работы инструмента Многомерная кластеризация по умолчанию является новый выходной класс объектов, содержащий поля, используемые в анализе, а также новое целочисленное поле CLUSTER_ID, содержащее информацию о том, какому кластеру каждый объект принадлежит. Этот выходной класс объектов добавляется в таблицу содержания с уникальной цветовой схемой отображения, которая применяется к полю CLUSTER_ID. Поле IS_SEED показывает, какие объекты использовались как исходные объекты для наращивания кластеров.
Выходные данные диаграммы инструмента Многомерная кластеризация
Для суммирования созданных кластеров создается несколько типов диаграмм. Ящичковые диаграммы применяются для показа информации как о каждом из кластеров, так и о каждой переменной анализа. Ниже показано изображение, которое поможет вам анализировать ящичковые диаграммы и их суммарные значения для каждого Поля анализа и созданного кластера: минимальное значение данных, 1й квартиль, глобальная срединное значение, 3й квартиль, максимальное значение данных, и выбросы в данных (значения, меньшие или большие умноженного на 1.5 значения межквартильного размаха). Остановите курсор на ящичковой диаграмме, чтобы увидеть эти значения, а также значение межквартильного размаха. Все отметки, не попадающие в верхний или нижний ящичек (не находящиеся между минимумом и максимумом), представляют собой выбросы в данных.
Более подробно:
Межквартильный размах (IQR) – разность между 3м и 1м квартилем. Нижние выбросы – это значения меньше 1,5*IQR (Q1-1,5*IQR), а верхние выбросы – это значения больше 1,5*IQR (Q3+1,5*IQR). Выбросы отображаются на ящичковых диаграммах как символы точек.
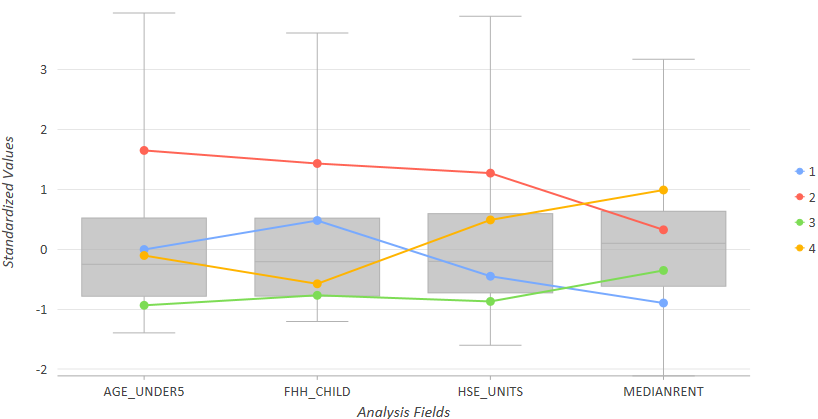
В параллельной ящичковой диаграмме представлена сводка по кластерам и переменным в них. К примеру, инструмент Многомерная кластеризация был запущен на переписных участках для создания четырех кластеров. На показанном ниже изображении кластер 2 (красный) соответствует участкам с арендной платой выше среднего по сравнению с другими кластерами, самыми высокими значениями домовладений женщин с детьми (FHH_CHILD), самыми высокими значениями количества жилых помещений (HSE_UNITS) и самыми высокими значениями количества детей возрастом до 5 лет. Кластер 4 (золотисто-красный) отражает участки с самой высокой медианной арендной платой, практически с самым низким числом домовладений женщин с детьми, и большим, чем в среднем, числом жилых помещений. Кластер 3 (зеленый) соответствует участкам с самым низким числом домовладений женщин с детьми, самыми низкими значениями количества детей возрастом до 5 лет, минимальным числом жилых помещений и невысоким уровнем арендной платы (но выше, чем в кластере 1). Остановите курсор над каждым узлом средних линий, чтобы увидеть среднее значение кластера для каждого Поля анализа.
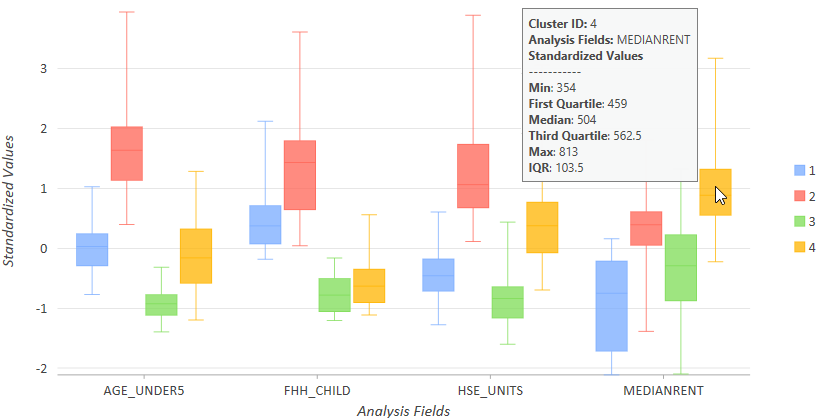
После изучения основной информации об анализе с параллельными ящичковыми диаграммами вы можете изучить ящичковые диаграммы каждого кластера для каждой переменной, выбрав Рядом на вкладке Серии панели Свойства диаграммы. В этом представлении данных легко увидеть, у какой группы наибольший и наименьший диапазон значений для каждой переменной. Для каждой переменной каждого кластера будет создана ящичковая диаграмма, и вы сможете увидеть, как связаны значения всех кластеров между собой. Поместите курсор над ящичковой диаграммой каждой переменной, чтобы увидеть минимальное, максимально и среднее значение для каждой переменной каждого кластера. На показанной ниже диаграмме вы увидите, что Кластер 4 (золотистый) характеризуется высочайшими значениями переменной MEDIANRENT и содержит участки с диапазоном значений от 354 до 813.
Также создается столбчатая диаграмма, показывающая число объектов в кластерах. При выборе каждого столбца будет также выбраны объекты на карте, что может вам помочь для выполнения последующего анализа.
Если вы оставляете пустым параметр Число кластеров, инструмент вычислит оптимальное для ваших данных количество кластеров. Если вы укажете путь для Выходной таблицы оценки числа кластеров, будет создана диаграмма с вычисленными значениями Псевдо-F-статистики. Высочайший пик графика – это наибольшая F-статистика, указывающая наиболее эффективное число групп для различения указанных объектов и переменных. На следующем графике F-статистика, связанная с четырьмя группами, имеет наибольшее значение. Пять групп с большим значением псевдо-F-статистики также будут хорошим выбором.
Рекомендации
Хотя существует тенденция для включения максимально возможного числа Полей анализа, при использовании инструмента Многомерная кластеризация лучше начать с одной переменной. Результаты намного легче интерпретировать при меньшем числе полей анализа. Также легче определить, какие переменные лучше разделяют группы при меньшем количестве полей.
Во многих ситуациях вы запустите инструмент Многомерная кластеризация несколько раз в поисках оптимального Числа кластеров, наиболее эффективного сочетания Полей анализа, которые наилучшим образом объединяют ваши объекты в кластеры.
Если инструмент возвращает число 30 в качестве оптимального числа кластеров, обратите внимание на диаграмму F-статистики. Выбор числа кластеров и интерпретация графика F-статистики - особое умение, и вполне возможно, что меньшее число кластеров больше подойдет для вашего анализа.
Дополнительные источники
Для получения дополнительной информации обратитесь к следующим ресурсам:
- Caliński, T. and J. Harabasz. 1974. "Дендритовый метод для кластерного анализа." Коммуникации в статистике. 3:1, 1-27. https://doi.org/10.1080/03610927408827101.
- Hinde, A., T. Whiteway, R. Ruddick, and A. D. Heap. 2007. "Морские пейзажи австралийской границы и прилегающего морского дна: Методология нажатия клавиш". Geoscience Australia. Record 2007/10, 58pp.
- Jain, A. K. 2009. "Data Clustering: 50 years beyond K-Means." Pattern Recognition Letters. https://doi.org/10.1016/j.patrec.2009.09.011.