Когда мы смотрим на мир вокруг нас, мы автоматически организуем, группируем, дифференцируем и классифицируем то, что видим, чтобы лучше понять окружающие нас объекты. Такой тип ментальной классификации необходим для обучения и понимания. Аналогично, для лучшего изучения данных можно использовать инструмент Пространственно ограниченная многомерная кластеризация. Используя число создаваемых кластеров, инструмент ищет решение, в котором все объекты в каждом кластере максимально похожи, а сами группы максимально отличаются друг от друга. Сходство объектов основано на наборе атрибутов, указываемых для параметра Поля анализа, которые при необходимости могут накладывать ограничения на размер кластера. Алгоритм данного инструмента использует граф связности (минимальное связующее дерево) и метод SKATER для поиска естественных кластеров в ваших данных, а также накопление доказательств для оценки вероятности членства в кластере.
Подсказка:
Кластеризация, группировка и классификация - самые часто используемые методы машинного обучения. Инструмент Пространственно ограниченная многомерная кластеризация использует методы обработки «без обучения» для нахождения естественных кластеров ваших данных. Эти методы классификации называются классификацией «без обучения», так как не требуют набора классифицированных заранее объектов для «тренировки» алгоритма для дальнейшего поиска кластеров в ваших данных.
Хотя существует множество алгоритмов кластерного анализа, все из них классифицируются как NP-трудными. Это означает, что единственный способ гарантировать, что решение идеально максимизирует сходства в группе и различия между группами – перепробовать все возможные комбинации объектов, которые требуется разбить на кластеры. Хотя этого можно добиться при небольшом количестве объектов, задача быстро становится трудноразрешимой.
При этом не только нельзя найти оптимальное решение, но также нельзя определить алгоритм группировки, который будет работать лучше всего для всех возможных сценариев. Кластеры бывают разных форм, размеров и плотностей. Атрибуты могут содержать данные с различными диапазонами, симметрией, непрерывностью и единицами измерений. Это объясняет, почему за последние 50 лет было разработано столько разных алгоритмов кластеризации. Инструмент Пространственно ограниченная многомерная кластеризация следует рассматривать как исследовательский инструмент, позволяющий узнать больше о структурах в ваших данных.
Возможное применение
Некоторые способы использования этого инструмента перечислены ниже:
- Если вы собрали данные о наблюдении за животными для лучшего понимания территории их обитания, то и здесь инструмент Пространственно ограниченная многомерная кластеризация может оказаться полезным. Знания о том, где и когда собираются стаи лосося, например, могут помочь в проектировании защищенных областей для обеспечения успешного нереста.
- Агрономам может потребоваться классифицировать разные типы почвы на изучаемой территории. Используя инструмент Пространственно ограниченная многомерная кластеризация с характеристиками почвы, полученными из ряда образцов, можно определить кластеры разных, пространственно непрерывных типов почв.
- Группируя клиентов на основе покупательских предпочтений, демографических характеристик и закономерностей перемещения, можно создать эффективную маркетинговую стратегию для продукции вашей компании.
- Службам городского планирования часто нужно разделять города на районы, чтобы эффективно размещать муниципальные учреждения и развивать локальные сообщества. Используя инструмент Пространственно ограниченная многомерная кластеризация с физическими и демографическими характеристиками городских кварталов, службы городского планирования могут определить пространственно непрерывные области города со схожими физическими и демографическими характеристиками.
- Экологическая ошибка – это известная задача статистического влияния при выполнении анализа на агрегированных данных. Часто схема агрегирования, используемая для анализа, никак не соотносится с тем, что нужно анализировать. Данные переписи, например, агрегируются на основе распределения населения, что может быть не лучшим вариантом для анализа лесных пожаров. Разбиение наименьших единиц агрегирования на однородные регионы с набором атрибутов, точно отражающих аналитические задачи – это эффективный метод, позволяющий сократить влияние агрегирования и избежать экологической ошибки.
Входные данные
Этот инструмент принимает точечные или полигональные входные объекты, путь к Выходному классу объектов, одно или несколько Полей анализа, целочисленное значение Числа кластеров, которые требуется создать, и тип Пространственного ограничения, который применяется с алгоритмом группировки. Существует также несколько дополнительных параметров, использующихся для задания Ограничения размера кластера либо для минимального или максимального числа объектов в кластере, либо минимальной или максимальной суммы атрибутов кластера и Выходная таблица оценки оптимального числа кластеров.
Поля анализа
Выберите числовые поля, которые отражают относительные, интервальные или порядковые системы измерений. Хотя номинальные данные могут быть представлены с помощью бинарных переменных, это обычно не работает, как и другие числовые типы переменных. Например, можно создать переменную Rural и назначить каждому объекту (например, каждому смежному кварталу переписи) значение 1, если это сельский объект, или значение 0, если это городской объект. Лучший пример применения этой переменной с инструментом Пространственно ограниченная многомерная кластеризация – это количество или часть площади сельскохозяйственных угодий, связанная с каждым объектом.
Примечание:
Значения в Полях анализа стандартизируются инструментом, так как переменные с большой вариабельностью (большим распределением данных относительного среднего) по всей видимости оказывают большее влияние на кластеризацию, чем переменные с небольшой вариабельностью. Нормализация значений атрибутов включает z-трансформацию, где средняя величина всех значений вычитается из каждого значения и делится на стандартное отклонение, вычисленное для всех значений. Стандартизация расставляет все эти атрибуты на одни весы, даже когда они представлены совершенно разными типами чисел: коэффициентами (от 0 до 1,0), численностью население (значение свыше 1 миллиона) и расстояниями (например, километрами).
Необходимо выбрать переменные, которые, по вашему мнению, будут отличать один кластер объектов от другого. Предположим, вы хотите сгруппировать школьные округа по успеваемости учеников в стандартных тестах. Вы можете выбрать Поля анализа, такие как общие оценки по тестам, результаты для каждого предмета, например математика или литература, процент учеников, получивших минимальную оценку по тесту, и т. д. При запуске вами инструмента Пространственно ограниченная многомерная кластеризация для каждой переменной вычисляется значение R2 и передается в окно сообщений. В сводных данных ниже, школьные округа сгруппированы на основе баллов учеников, набранных при тестировании, процента взрослых, которые не окончили среднюю школу, затрат на каждого ученика и среднего соотношение числа учеников и учителей. Обратите внимание, что у переменной TestScores самое большое значение R2. Это означает, что данная переменная наиболее эффективно разделяет школьные округа на кластеры. Значение R2 отражает, в какой степени вариация в исходных данных TestScores была сохранена в процессе группировки. Чем больше R2 для конкретной переменной, тем лучше переменная различает ваши объекты.

Более подробно:
R2 вычисляется следующим образом:
(TSS – ESS) / TSSГде TSS – общая сумма квадратов, а ESS – объясненная сумма квадратов. TSS вычисляется за счет возведения в квадрат и суммирования отклонений от глобального среднего значения для переменной. ESS вычисляется одинаково, только отклонения применяются по группам: каждое значение вычитается из среднего значения для группы, которой оно принадлежит, а затем возводится в квадрат и суммируется.
Ограничения размера кластера
Размером кластеров можно управлять с помощью параметра Ограничения размера кластера. Можно задать для кластера минимальный или максимальный порог. В качестве ограничения размера можно использовать Число объектов, которое должен содержать каждый кластер, или сумму Атрибутивных значений. К примеру, если вы выполняете кластеризацию округов США , основываясь на ряде экономических переменных, вы можете задать, что минимальное население каждого кластера - 5 млн человек, а максимальное население - 25 млн человек. Либо можно указать, что в каждом кластере может быть не меньше 30 округов.
Если задано ограничение Максимальное число для кластера, алгоритм начнет работу с одного кластера и будет разбивать его на соседние друг с другом кластеры с похожими значениями. Новые кластеры будут создаваться до тех пор, пока размеры всех кластеров не станут меньше максимального числа для кластера, учитывая все переменные для разбиения.
SKATER формирует кластеры, разбивая данные с близкими к интересующим объектам значениями. Возможно, что Ограничение размера кластера не будет соблюдено для всех кластеров. Это может произойти в случае, когда ограничения размера кластера не привели к созданию оптимальных кластеров
SKATER формирует кластеры, пространственно разбивая данные с близкими значениями всех указанных Полей анализа. Возможно, что Ограничение размера кластера не будет соблюдено для всех кластеров. Это может быть связано с тем, что для максимального и минимального ограничения были заданы близкие значения или из-за способа создания минимального связующего дерева на основе пространственных ограничений. В этом случае работа инструмента прекратится и о кластерах, не удовлетворяющих заданным требованиям, появится информация в окне сообщений.
Число кластеров
Иногда вы можете точно знать количество кластеров, которое лучше всего подходит для вашей задачи. Например, если у вас пять менеджеров по продажам, и вы хотите назначить каждому из них собственный регион, вы используете значение 5 для параметра Число кластеров. Но во многих случаях критерий для выбора точного числа кластеров не доступен. Вместо этого вам нужно получить число, которое лучше всего позволяет классифицировать сходства и различия объектов. В этой ситуации можно оставить пустым значение Число кластеров и позволить инструменту Пространственно ограниченная многомерная кластеризация оценить эффективность деления объектов на 2, 3, 4 и до 30 групп. Эффективность кластеризации измеряется с помощью псевдо-F-статистики Калински-Харабаза, которая является отношением вариации между кластерами к вариации внутри кластера: Другими словами, то отношение схожести объектов внутри группы к различию объектов между группами:

Предположим, вы хотите создать четыре смежных кластера. В этом случае инструмент создаст минимальное остовое дерево, отражающее как пространственную структуру ваших объектов, так и связанные с ними значения полей анализа. Затем инструмент определит наилучшее место разрезания дерева для получения двух отдельных кластеров. Далее он определит, какой из двух получившихся кластеров должен быть разделен для получения трех групп наилучшим способом. Один из двух кластеров будет разделен, второй останется неизменным. Наконец, он определит, какой из трех получившихся кластеров должен быть разделен, чтобы получить четыре наилучших кластера. При каждом делении наилучшим решением считается то, при котором возрастает схожесть внутри кластеров и различие между ними. Кластер больше не может быть разделен (кроме произвольного деления), когда значения полей анализа всех объектов внутри кластера являются идентичными. В случае, когда все полученные кластеры имеют идентичные объекты, инструмент пространственно ограниченная многомерная кластеризация прекращает создание новых кластеров, даже если не достигнуто заданное Числа кластеров. Когда все Поля анализа имеют идентичные значения, основание для разделения кластера отсутствует.
Пространственные ограничения
Параметр Пространственные ограничения позволяет быть уверенными в том, что полученные кластеры будут пространственно близкими. Опции Смежности включены для полигональных классов объектов и указывают, что объекты могут входить в один кластер, только если у них есть общее ребро (Только совпадающие ребра или общее ребро или вершина (Совпадающие углы ребер) с другим участником кластера. Опции непрерывности полигонов – это не очень хороший выбор, но если набор данных содержит кластеры несмежных полигонов или полигонов без смежных соседей.
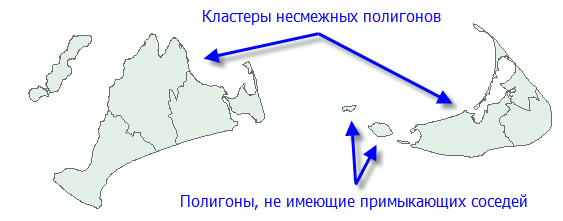
Опция Усовершенствованная интерполяция Делоне подходит для точечных и полигональных объектов и позволяет быть уверенным в том, что объект включается в кластер, только если хотя бы один другой его объект является естественным соседом (триангуляция Делоне). Концептуально, метод триангуляции Делоне создает сеть не перекрывающихся треугольников на основе центроидов объектов. Каждый объект – это узел треугольника, а узлы с общими ребрами считаются соседями. Это треугольники затем обрезаются выпуклым многоугольником, так чтобы объекты не соседствовали с объектами вне этого многоугольника. Опцию не следует использовать для наборов данных с совпадающими объектами. Кроме того, так как метод триангуляции Делоне преобразует объекты в полигоны Тиссена для определения соседских отношений, особенно когда в наборе данных есть полигональные объекты и иногда периферийные объекты, результаты использования этой опции не всегда будут ожидаемыми. На рисунке ниже обратите внимание, что некоторые группы исходных полигонов не являются смежными. Однако при их конвертации в полигоны Тиссена все сгруппированные объекты по факту имеют смежные ребра.

Если полученные группы должны быть близкими в пространстве и времени, создайте файл матрицы пространственных весов (SWM) с помощью инструмента Построить матрицу пространственных весов и выберите Пространственно-временное окно для параметра Определение пространственных взаимоотношений. Затем можно указать созданный с помощью инструмента Построить матрицу пространственных весов SWM-файл в параметре Файл матрицы весов при запуске инструмента Пространственно ограниченная многомерная кластеризация.
Примечание:
Хотя пространственные отношения между объектами хранятся в SWM-файле и используются инструментом Пространственно ограниченная многомерная кластеризация для наложения пространственных ограничений, фактически взвешивания не происходит. SWM-файл используется только для отслеживания того, какие объекты можно, а какие нельзя включить в один кластер.
Минимальное остовое дерево
При указании пространственного ограничения, чтобы включать в группу смежные или близкие объекты, инструмент сначала формирует граф связности, представляющий соседские отношения объектов. На основе графа связности формируется минимальное остовое дерево, которое отражает и пространственные отношения объектов, и сходство данных объектов. Объекты становятся узлами в минимальном остовом дереве, связанном взвешенными ребрами. Вес каждого ребра пропорционален сходству объектов, которые он соединяет. После создания минимального остового дерева ветвь (ребро) дерева обрезается, после чего мы получаем два минимальных остовых дерева. Обрезаемое ребро выбирается так, чтобы минимизировать расхождение в полученных кластерах, избегая при этом получения кластеров, состоящих из одного объекта. При каждой итерации одно из минимальных остовых деревьев делится этим процессом обрезки до получения указанного Числа кластеров. Опубликованный метод называется SKATER (пространственный кластерный анализ с удалением ребра дерева). Хотя на каждой итерации выбирается ветвь, оптимизирующая сходство объектов в группе, нельзя гарантировать, что конечный результат будет оптимальным.
Вероятность участия
Параметр Перестановки для расчета вероятности членства задает число необходимых перестановок для вычисления вероятности членства накоплением доказательств. Вероятности членства включатся в выходной класс объектов в поле PROB. Высокая вероятность членства означает, что объект похож и близок к кластеру, к которому он присвоен, и вы можете быть уверены в принадлежности объекта кластеру. Низкая вероятность говорит о том, что объект сильно отличается от кластера, которому он присвоен алгоритмом SKATER либо объект должен быть включен в другой кластер, если изменились Поля анализа, Ограничения размера кластера или Пространственные ограничения.
Число заданных вами перестановок определяет число остовых деревьев создаваемых для нарушения пространственного ограничения SKATER. Тогда алгоритм работает для заданного Числа кластеров для каждого случайного остового дерева. Используя кластеры, определенные алгоритмом SKATER, процесс перестановки отслеживает частоту слияния членов кластера при изменении остовых деревьев. Объекты, меняющие кластеры из-за небольших изменений остового дерева, получают малые вероятности членства, а не меняющие кластеры - высокие значения вероятности членства.
Вычисление таких вероятностей для больших наборов данных может выполняться довольно долго. Рекомендуется сначала сделать несколько попыток и определить оптимальное число кластеров для анализа, а затем, при следующем запуске, вычислять вероятности. Вы можете улучшить производительность, увеличив значение Настройки параллельной обработки до 50.
Выходные данные
Число выходных объектов, создаваемых инструментом Пространственно ограниченная многомерная кластеризация. Сообщения можно просмотреть на панели Геообработка, поместив курсор на индикатор прогресса, щелкнув кнопку индикатора прогресса инструмента  инструмента либо развернув раздел сообщений в нижней части панели Геообработка. Вы можете получить доступ к сообщениям для выполненного ранее инструмента Пространственно ограниченная многомерная кластеризация на панели История геообработки.
инструмента либо развернув раздел сообщений в нижней части панели Геообработка. Вы можете получить доступ к сообщениям для выполненного ранее инструмента Пространственно ограниченная многомерная кластеризация на панели История геообработки.

Результатом работы инструмента Пространственно ограниченная многомерная кластеризация по умолчанию является новый выходной класс объектов, содержащий поля, используемые в анализе, а также новое целочисленное поле CLUSTER_ID, содержащее информацию о том, какому кластеру принадлежит каждый объект. Этот выходной класс объектов добавляется в таблицу содержания с уникальной цветовой схемой отображения, которая применяется к полю CLUSTER_ID.
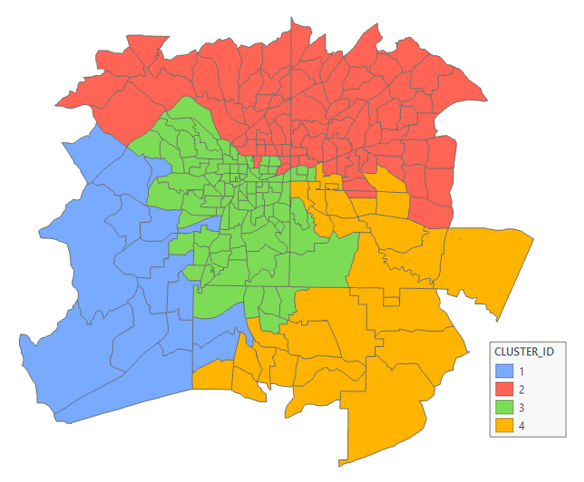
Выходные диаграммы пространственно ограниченной многомерной кластеризации
Для суммирования созданных кластеров создается несколько типов диаграмм. Ящичковые диаграммы применяются для показа информации как о каждом из кластеров, так и о каждой переменной анализа. Ниже показано изображение, которое поможет вам анализировать ящичковые диаграммы и их суммарные значения для каждого Поля анализа и созданного кластера: минимальное значение данных, 1й квартиль, глобальная срединное значение, 3й квартиль, максимальное значение данных, и выбросы в данных (значения, меньшие или большие умноженного на 1.5 значения межквартильного размаха). Остановите курсор на ящичковой диаграмме, чтобы увидеть эти значения, а также значение межквартильного размаха. Все отметки, не попадающие в верхний или нижний ящичек (не находящиеся между минимумом и максимумом), представляют собой выбросы в данных.
Более подробно:
Межквартильный размах (IQR) – разность между 3м и 1м квартилем. Нижние выбросы – это значения меньше 1,5*IQR (Q1-1,5*IQR), а верхние выбросы – это значения больше 1,5*IQR (Q3+1,5*IQR). Выбросы отображаются на ящичковых диаграммах как символы точек.

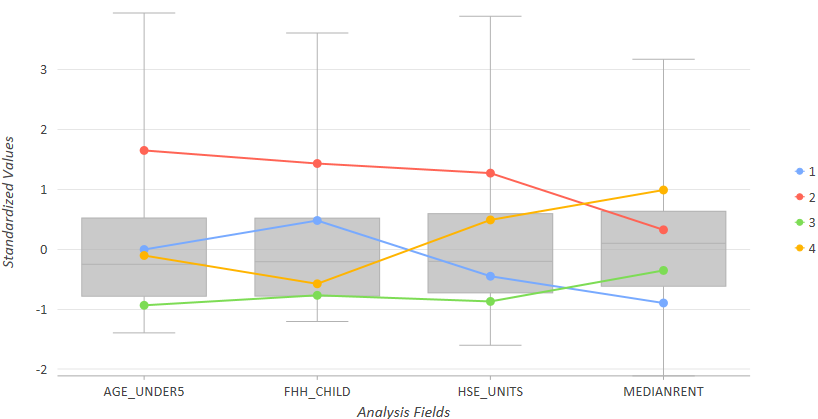
В параллельной ящичковой диаграмме представлена сводка по кластерам и переменным в них. К примеру, инструмент пространственно ограниченной многомерной кластеризации был запущен на переписных участках для создания четырех кластеров. Обратите внимание. Что на показанном ниже изображении кластер 2 (красный) соответствует участкам со средней арендной платой, высочайшими значениями домовладений женщин с детьми (FHH_CHILD), высочайшими значениями количества жилых помещений (HSE_UNITS) и самыми высокими значениями количества детей возрастом до 5 лет. Кластер 2 (золотисто-желтый) соответствует участкам с высокими средними значениями арендной платы, достаточно низким числом домовладений женщин с детьми и достаточно высоким количеством жилых помещений. Кластер 3 (зеленый) соответствует участкам с самым низким числом домовладений женщин с детьми, самыми низкими значениями количества детей возрастом до 5 лет, минимальным числом жилых помещений и невысоким уровнем арендной платы (но выше, чем в кластере 1). Остановите курсор над каждым узлом средних линий, чтобы увидеть среднее значение кластера для каждого Поля анализа.
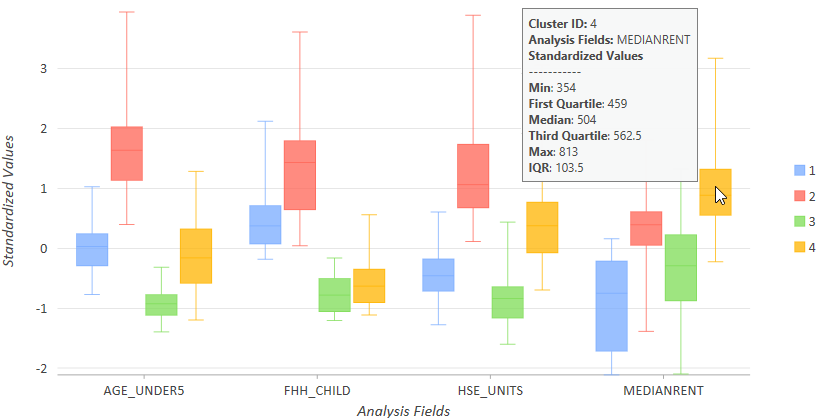
После изучения основной информации об анализе с параллельными ящичковыми диаграммами вы можете изучить ящичковые диаграммы каждого кластера для каждой переменной, выбрав Рядом на вкладке Серии панели Свойства диаграммы. В этом представлении данных легко увидеть, у какой группы наибольший и наименьший диапазон значений для каждой переменной. Для каждой переменной каждого кластера будет создана ящичковая диаграмма, и вы сможете увидеть, как связаны значения всех кластеров между собой. Поместите курсор над ящичковой диаграммой каждой переменной, чтобы увидеть минимальное, максимально и среднее значение для каждой переменной каждого кластера. На показанной ниже диаграмме вы увидите, что Кластер 4 (золотистый) характеризуется высочайшими значениями переменной MEDIANRENT и содержит участки с диапазоном значений от 354 до 813.
Также создается столбчатая диаграмма, показывающая число объектов в кластерах. При выборе каждого столбца будет также выбраны объекты на карте, что может вам помочь для выполнения последующего анализа.
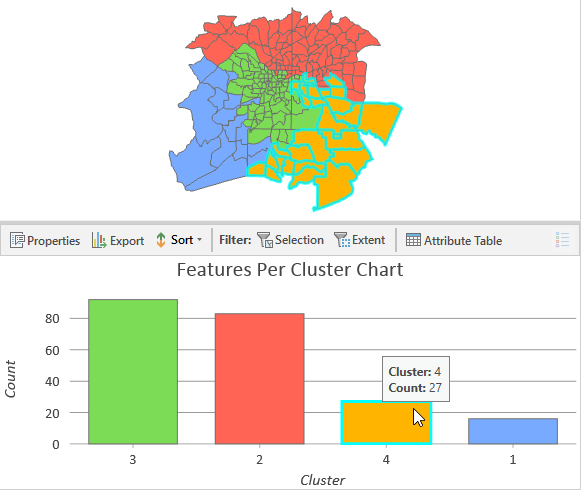
Если вы оставляете пустым параметр Число кластеров, инструмент вычислит оптимальное для ваших данных количество кластеров. Если вы укажете путь для Выходной таблицы оценки числа кластеров будет создана диаграмма с вычисленными значениями Псевдо-F-статистики. Высочайший пик графика – это наибольшая F-статистика, указывающая наиболее эффективное число групп для различения указанных объектов и переменных. На следующем графике F-статистика, связанная с четырьмя группами, имеет наибольшее значение. Пять групп с большим значением псевдо-F-статистики также будут хорошим выбором.

Рекомендации
Хотя существует тенденция для включения максимально возможного числа Полей анализа, при использовании инструмента Пространственно ограниченная многомерная кластеризация лучше начать с одной переменной. Результаты намного легче интерпретировать при меньшем числе полей анализа. Также легче определить, какие переменные лучше разделяют группы при меньшем количестве полей.
Во многих ситуациях вы запустите инструмент Пространственно ограниченная многомерная кластеризация несколько раз в поисках оптимального Числа кластеров, наиболее эффективных Пространственных ограничений и сочетания Полей анализа, которые наилучшим образом разбивают ваши объекты на группы.
Если инструмент возвращает число 30 в качестве оптимального числа кластеров, обратите внимание на диаграмму F-статистики. Выбор числа кластеров и интерпретация графика F-статистики - особое умение, и вполне возможно, что меньшее число кластеров больше подойдет для вашего анализа.
Дополнительные источники
Duque, J. C., R. Ramos, and J. Surinach. 2007. "Supervised Regionalization Methods: A Survey" in International Regional Science Review 30: 195–220.
Assuncao, R. M., M. C. Neves, G. Camara, and C. Da Costa Freitas. 2006. "Эффективные методы регионализации для социально-экономических географических единиц с использованием минимальных остовых деревьев" in International Journal of Geographical Information Science 20 (7): 797–811.