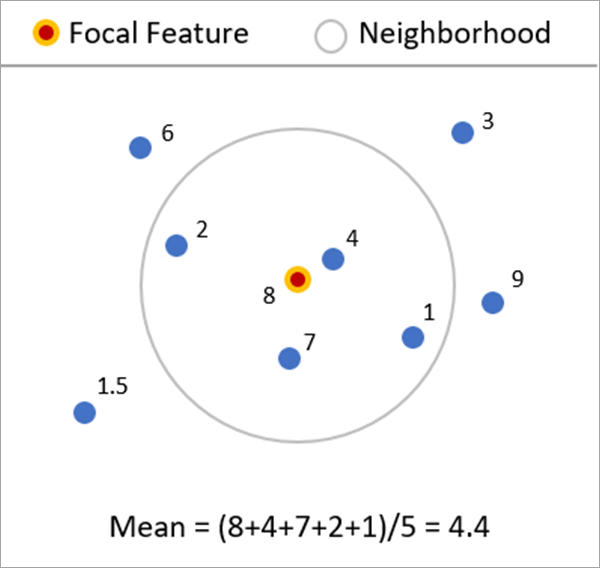
邻域汇总统计工具使用邻域计算点或面要素的一个或多个数字字段的局部汇总统计数据。局部统计数据包括平均值、中位数、标准差、四分位距、偏度和分位数不平衡。邻域包括距离范围、相邻要素的数目、面邻接和空间权重文件。您可以使用核在地理上加权所有局部统计数据。
邻域类型
邻域类型参数具有六个选项,可用于定义用作每个焦点要素的相邻要素的要素。
- 距离范围 - 将指定距离内的所有要素(最多 1,000 个)用作相邻要素。默认距离为确保每个要素至少包含一个额外邻域的最短距离。
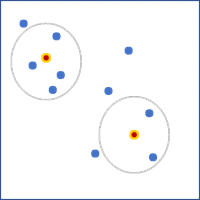
- 相邻要素的数目 - 将固定数量的最接近要素用作相邻要素。
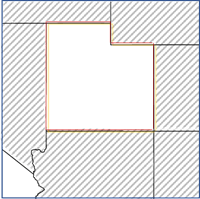
- 仅邻接边 - 与焦点要素共享边的任何面都将用作相邻要素。此选项仅适用于面要素。
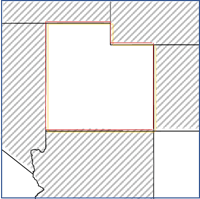
- 邻接边拐角 - 与焦点要素共享边或拐角的任何面都将用作相邻要素。此选项仅适用于面要素。
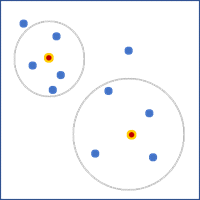
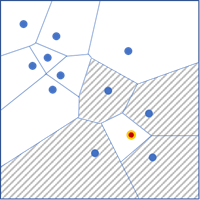
- Delaunay 三角测量 - 通过在 Delaunay 三角测量中共享边或拐角来定义相邻要素。使用此选项等于在点上使用创建泰森多边形工具,并在泰森多边形上使用邻接边拐角选项。此选项仅适用于点要素。
- 通过文件获取空间权重 - 每个要素的相邻要素和权重由在权重矩阵文件参数中指定的空间权重矩阵文件定义。您可以使用生成空间权重矩阵和生成网络空间权重工具。
汇总统计数据
可以为每个分析字段计算六个汇总统计数据(由局部汇总统计参数指定)。这六个统计数据包括中心性测量、变异性和分布测量以及对称性测量。每个类别提供两种统计数据:一种是传统统计数据,一种是可靠统计数据。可靠统计数据是不受少数异常值影响的统计指标。
在默认情况下,将使用局部汇总统计参数的全部选项,以便为每个分析字段计算全部六种统计数据。可在局部统计公式部分查看每种统计数据的公式。
中心性测量用于估计值分布的中间位置或中心。您可以使用这些选项来平滑噪点数据中的值。中心性测量如下:
- 平均值(传统)- 分析字段值的算术平均值。
- 中位数(可靠)- 分析字段值的第 50 个百分点。一半的值低于中位数,一半的值高于中位数。
变异性或分布测量用于估计可能值的分布范围。您可以使用这些选项调查整个地图上分析字段中的变异性是否相似(称为方差平稳性),或者某些区域的局部变异性是否高于其他区域。变异性测量如下:
- 标准差(传统)- 分析字段中值的标准差。
- 四分位距(可靠)- 分析字段值的中间一半的范围(第 75 个百分点减去第 25 个百分点)。有一半的数据位于此范围内。
对称性测量用于测量分布的形状是否围绕中间区域对称。这些选项可用于调查极高和低极值的出现频率。对称性测量如下:
- 偏度(传统)- 分析字段值的偏度。
- 分位数不平衡(可靠)- 介于 -1 到 1 之间的值,指示中位数相对于第 25 个百分点和第 75 个百分点的位置。接近 -1 的值表示中位数接近第 25 个百分点,接近 1 的值表示中位数接近第 75 个百分点。接近 0 的值表示对称,即中位数介于第 25 个百分点和第 75 个百分点之间。
工具输出
使用在局部汇总统计参数中指定的针对第一个提供的分析字段(如果未提供分析字段,则为到相邻要素的距离)计算的统计数据在地图中表示输出要素。如果您为局部汇总统计选择全部,则要素将显示平均值统计数据的结果。所有其他分析字段的汇总统计数据将与所有分析字段的副本一同另存为输出要素中的字段。还有一些字段指示每个分析字段使用的相邻要素数目。
地理加权汇总统计数据
当将邻域类型参数指定为距离范围或相邻要素的数目时,可以使用局部权重方案参数对所有统计数据进行地理加权。如果将邻域类型参数指定为通过文件获取空间权重,则文件中指定的权重将用作权重方案。如果应用权重方案,则会对所有汇总统计数据进行加权,以使用称为核的函数使更靠近焦点要素的相邻要素在计算中获得更高的权重,随着与焦点要素的距离变大,权重会变低。局部权重方案参数中提供了两个核函数。
- 双平方
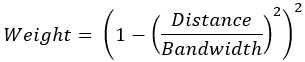
- 高斯函数
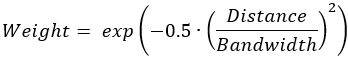
核函数取决于控制权重随距离减少的速度的带宽。每个核的带宽在核带宽参数中提供。如果您不提供值,系统会在运行时估计一个默认值,并将其显示为地理处理消息。有关如何计算此默认带宽的信息,请参阅核密度分析的工作原理。
注:
对于距离范围邻域,默认核带宽为与距离范围参数相同的值。
局部统计数据公式
本部分包含单个焦点要素所有加权和未加权版本的汇总统计数据公式。这些公式适用于所有分析字段的每个输入要素。
在所有公式中,i = 1, ..., n 为值 (xi) 按升序排序的焦点要素相邻要素(可能包含焦点要素本身)。在应用这些公式之前,所有加权 (wi) 已归一化为总和。每个统计数据的未加权版本是通过为所有相邻要素 i 设置 wi = 1/n 得出的。
传统统计数据
下表显示了每个传统汇总统计数据的加权和未加权版本。
| 统计数据 | 加权公式 | 未加权公式 |
|---|---|---|
平均值 | 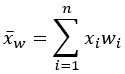 | 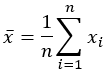 |
标准差 | 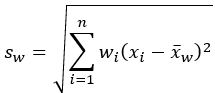 | 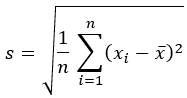 |
偏度 | 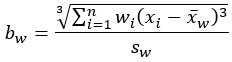 | 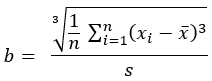 |
可靠统计数据
所有可靠统计数据都取决于加权的 p 分位数定义,其中 p 介于 0 和 1 之间。此定义用于计算加权中位数 (p=0.5),第一个四分位数 (p=0.25) 和第三个四分位数 (p=0.75)。给定 p 的 p 分位数定义如下:
- 加权 p 分位数:
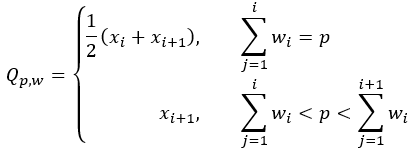
- 未加权 p 分位数:
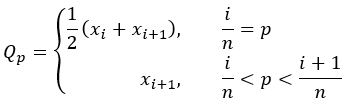
根据上述的 p 分位数定义,下表显示了每个可靠汇总统计数据的加权和未加权版本。
| 统计数据 | 加权公式 | 未加权公式 |
|---|---|---|
中值 | 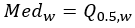 | 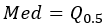 |
四分位距 | 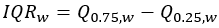 | 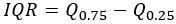 |
分位数不平衡 | 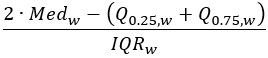 | 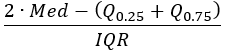 |
其他资源
有关地理加权汇总统计数据的更多信息,请参阅以下参考:
- Brunsdon, C., Fotheringham, A.S., Charlton, M. (2002). "Geographically weighted summary statistics — a framework for localised exploratory data analysis." Computers, Environment and Urban Systems, 26(6): 501-524. ISSN 0198-9715. https://doi.org/10.1016/S0198-9715(01)00009-6.