需要 Spatial Analyst 许可。
可通过一组概念性步骤来帮助您构建模型。 要了解各个步骤的顺序,请您遵照以下指示解决一个示例问题。 作为一名城镇规划师,您分配到了一个为新学校寻找合适地点的任务。 将 ArcGIS Spatial Analyst 扩展模块中的各种工具结合使用将有助于您找出适合的地点。
步骤 1:陈述问题
要解决空间问题,首先需要对所要尝试解决的问题和所要达成的总体目标做出陈述。 因此,要先决定该项研究的预期输出,以便使所要生成的地图类型形象化。
您的问题是为新学校寻找最佳设址地点。 您需要生成两个地图。 第一个地图用于确定每个地点相对于彼此的适宜性,也称为适宜性地图。 第二个地图派生自适宜性地图,用于确定用于构建学校的实际位置,以满足学校的功能需求(规模和所需形状)。 要创建上述两个地图,需要生成加权适宜性模型。
为帮助您对该空间问题进行建模,这里将绘制一幅包含了各个步骤的示意图。 首先应对问题进行明确。 逐步解决问题的过程中,该示意图将逐渐得到扩展,这样便可以显示各个具体目标、过程模型和实现最终目的所需的输入数据集。
步骤 2:分解问题
明确问题后,请就问题内容进行进一步细分,直至了解解决此问题所需的各个步骤。 这些步骤便是您需要实现的具体目标。
定义具体目标时,要考虑以何种方式对各目标进行衡量。 如何衡量什么样的区域最适合建新学校? 对于这个假设的学校选址示例,其驱动因素是最大程度降低开发成本。 与已进行一些开发的区域相比,根据某些土地利用类型(例如目前的空旷区域)构建学校的成本更低。 另一个因素是地形,因为在平坦区域上构建学校通常比在斜坡上更容易。 由于很多迁到城镇居住的家庭都有小孩,因此最好将学校建于休闲娱乐设施的附近。 要对整个城镇的资源进行分配,选择远离现有学校的地点非常重要。 考虑学校的功能要求,需要寻找一块足以容纳该学校及其操场的区域。 显然还有更多可以包含在此例中的目标,例如,购买土地的费用,或者寻找一块适龄儿童密度最高的区域,但为方便起见,对此模型进行了简化。
要实现这些具体目标,您最好了解以下内容:
- 这些地点的土地利用类型是否适宜?
- 哪些地点的土地相对平坦?
- 这些地点是否足够接近休闲娱乐场所?
- 它们是否距离各现有学校足够远?
这些地点的土地利用类型是否适宜?
您需要确定何种土地利用类型适于建造学校。 这是一个因问题而异的比较主观的过程。 对于本例,在农业用地上建校被认为是最经济的,因此也是最合适的。 接下来依次是荒地、矮灌木丛、森林,排在最末的则是现存建筑用地。 此处不涉及任何过程模型,只需确定土地利用输入数据集以及最适于建校的土地利用类型。
- 所需的输入数据集:土地利用
哪些地点的土地相对平坦?
要查找相对平坦的表面区域,您需要创建一个能够显示表面坡度的地图。 此处的过程模型便涉及表面坡度的计算。
- 所需的输入数据集:高程
这些地点是否足够接近休闲娱乐场所?
由于学校最好建在休闲娱乐设施附近,因此需要创建可以显示到各休闲娱乐场所距离的地图,从而大概地将学校地址确定在附近区域。 此处的过程模型将涉及到计算与休闲娱乐场所的距离。
- 所需的输入数据集:休闲娱乐设施的位置数据
它们是否距离各现有学校足够远?
您需要将学校建在远离现有学校的地方,以避免位于这些学校的招生区范围内。 因此,您还需要创建一个可以显示与现有学校之间距离的地图。 此处的过程模型将涉及到计算与现有学校之间的距离。
- 所需的输入数据集:现有学校的位置数据
步骤 3:探索输入数据集
将问题分解为一系列具体目标和过程模型并且确定了所需的数据集之后,您应探索输入数据集了解其内容。 包括了解数据集内部和各个数据集之间的哪些属性对于解决问题来说比较重要,还包括查找数据的变化趋势。
通过探索数据,您通常可以更深入地了解要建校的区域、各输入属性的权重以及对建模过程进行的改动。 您将看到现有学校和休闲娱乐场所的位置,还可以通过高程数据集判断出高程较高的位置。 而通过土地利用数据集可了解该区域中与其他数据集相关的土地利用类型以及这些类型的土地的位置。
步骤 4:执行分析
您已确定了具体目标、各种元素及它们之间的交互作用、过程模型以及所需的输入数据集。 现在便可以执行分析了。
Esri GIS 分析手册中介绍了 ArcGIS 可以解决的多项任务,可通过 Esri Press  获取此手册。
获取此手册。
以下为该示例的一般流程图,用于确定拟建新学校的理想位置。 随附文本将介绍每个步骤的详细信息。
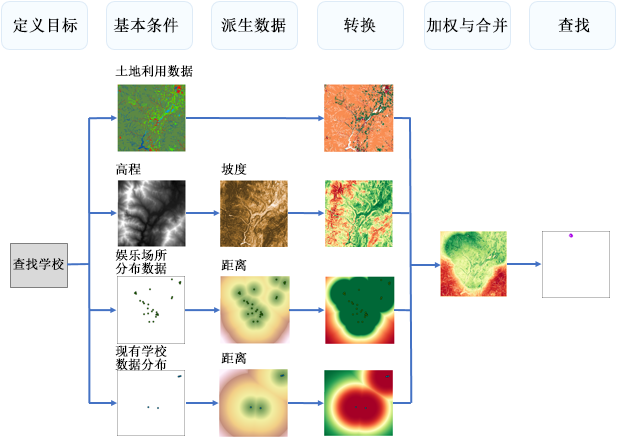
创建适宜性地图
创建适宜性地图可使您获悉地图上每个位置的适宜性值。
获得分析必要的数据集图层(在此示例中,分别为土地利用、坡度、到休闲娱乐场所的距离和到学校的距离)后,如何将这些图层加以结合从而创建出呈现建校候选区域的单一分级地图? 您需要了解如何比较各图层间的值。 可以通过以通用比例转换不同数据集内的值来实现上述操作。
各图层中的位置将按照作为新学校校址的适宜程度进行分级。 例如,您可以为每个图层中的各个位置指定一个 1 到 10 范围内的值,其中 10 表示最合适的校址。
这通常被称为适宜性范围。 可使用 NoData 将不予考虑的区域屏蔽掉。 同一数值范围内出现的所有测量结果在确定最适宜地点时均具有同等重要性。 模型最初便是通过这种方法构建的。 然后,在测试替代方案时,还可将不同权重系数应用于各图层以便进一步研究数据及数据之间的关系。
创建适宜性范围
如本例所示,适宜性范围的测量单位大多是合成的。 无论适宜性范围采用的是何种测量单位,每种测量单位都是对于适宜性或优先级的分级度量,按适宜程度从高到低进行排列。 单位的选择取决于您所测量的对象,例如到学校的距离。 但是,在很多情况下,还是要主观判断要建立的学校与另外某个学校之间特定距离的适宜程度。
通常存在一些固有的测量单位,它们与某些具体目标相关。 成本就是一个很好的示例,但需要对其进行足够细致地定义。 在一项建筑物适宜性的研究中,要实现房地产低成本的目标,成本将以“元”进行度量。 请确保该范围得到充分定义。 因为众所周知的“元”还存在其他变体,例如美元、澳元,或者货币之间的汇率。
虽然通常为了节省时间和金钱或因为未考虑到所有可能性而以线性关系的方式表示范围,但很多范围并不属于线性关系。 例如,如果为行程距离指定了一个范围,步行 1 千米、5 千米或 10 千米的适宜性等级则不能被分别划分为 10、5 和 1。 因为有些人可能认为步行 5 千米的不便程度仅是步行 1 千米的两倍,而其他人则可能会认为是 10 倍。
设计适宜性范围时,应与专家一起找出适宜性最佳和最差的点并且中间点越多越好。 专家应该会对正在研究的目标了如指掌。 例如,与其就交通状况最差的时间询问市政官员,让乘坐公交车上下班的人根据乘车需要提出意见更为明智。
有关处理冲突目标和评估标准的详细信息,请参阅由 Jacek Malczewski 所著的《GIS 和多标准决策分析》(GIS and Multicriteria Decision Analysis)。
划分输入等级
各种输入准备就绪后,需要将其转化为通用比例。
按照土地利用类型的适宜性为各区域划分等级
要在表示土地利用类型的地图中划分等级,请使用重分类工具。 由于涉及到成本,最好是建在某些土地利用类型上,因此您需要确定如何为各个值划分等级。
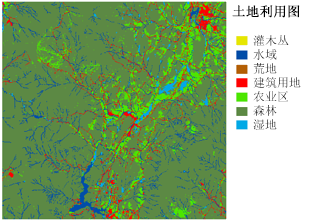
而此处您则需要确定哪种土地利用类型较好。 这是一个因研究而异的主观性问题。 确定哪类土地更适合建校而哪类土地不适合建校的最简单方法是,先确定最适合的土地类型再确定最不适合的土地类型。 然后,再从剩下的土地利用类型中确定最适合的类型和最不适合的类型。 持续执行此操作直到将各土地利用类型按优先级顺序排列。 土地利用类型中的水域和湿地已从分析中排除,因为无法在水上建校,并且对于在湿地上修建建筑也有一些限制。 下图显示了为土地利用类型划分等级的方式。
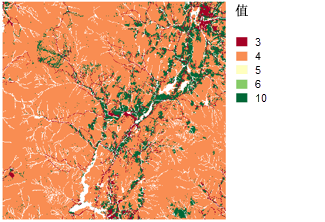
为相对平坦的区域划分等级
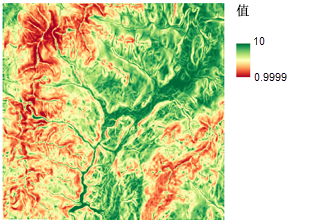
为避开陡坡而找出相对平坦的区域建校,您需要知道土地的坡度。 使用坡度工具为每个像元确定出它们到相邻像元值的最大变化率便可创建这样的地图。 生成的栅格将以连续变化的浮点值来记录坡度。 由于优先级直接随坡度值的变化而变化,因此可通过应用 Linear 函数,使用按函数重设等级工具在地图中划分等级。 由于建校地点最好位于相对平坦的区域,因此可以指定值 1 表示陡坡位置,值 10 表示缓坡位置。 将以线性方式调整中间值,如下图所示。

为接近休闲娱乐场所的区域划分等级
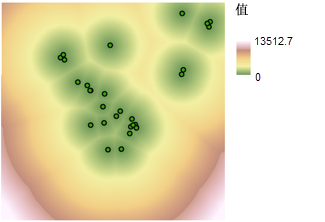
要将学校建在接近休闲娱乐设施的地方,您需要测量到这些休闲娱乐设施的距离。 使用欧氏距离工具计算出任意地点到最近的休闲娱乐场所的直线(欧氏)距离便可创建这样的地图。 得到的结果是一个栅格数据集,其中每个像元均表示到最近的休闲娱乐场所的距离。 由于输入值表示连续距离,因此要在此地图中划分等级,请使用按函数重设等级工具。 由于最好是建在接近休闲娱乐场所的地点,因此需要应用 MSSmall 函数。 越接近休闲娱乐场所的位置,将分配的优先值越高,而越远离休闲娱乐场所的位置,将分配的优先值越低。 到休闲娱乐场所的距离每隔一米,优先级便会随之变化,如下图所示。
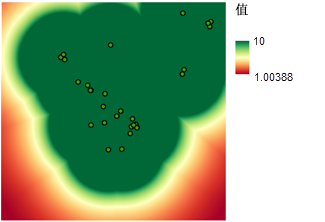
为远离现有学校的各个区域划分等级
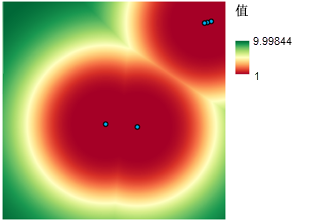
为避开其他学校的招生区,需要获知建校位置与这些学校的距离。 使用欧氏距离工具计算出任意地点到最近的学校的直线距离便可创建这样的地图。 得到的结果是一个栅格数据集,其中每个像元均表示到最近的学校的距离。 要在此地图中划分等级,请再次使用按函数重设等级工具。 由于建校地点最好远离现有学校,因此将使用 Large 函数,将到现有学校距离最近的值设为 1,将到现有学校距离最远的值设为 10。 在 Large 函数中,距离现有学校的距离增大一米,则优先级将随之增大,如下图所示。

合并适宜性地图
适宜性模型的最后一步是结合土地利用类型、坡度、与休闲娱乐场所的距离以及到学校的距离的变换输出(适宜性地图)。
要强调适宜性建模中某些具体目标的重要性,您可以对数据集进行加权,即将模型中对结果的影响力较重要数据集的百分比(权重)设为比其他数据集高。 如果所有数据集的重要性相同,则可以为每个数据集指定相同的权重。
在本例中,在分解问题的过程中您了解到最希望满足的具体目标是将学校建在接近休闲娱乐设施的地点,接下来才是远离现有学校的地点。 以下影响力的百分比将被指定给各个适宜性地图。 括号中的值是由百分数除以 100 而得来,这样各个值便可以标准化。 此归一化值将用作每个适宜性地图的乘数。
适宜性百分比
| 适宜性系数 | 影响力的百分比 | 标准化的百分比 |
|---|---|---|
到休闲娱乐场所的分级距离 | 50% | (0.5) |
到学校的分级距离 | 25% | (0.25) |
分级坡度 | 12.5% | (0.125) |
分级土地利用类型 | 12.5% | (0.125) |
到休闲娱乐场所的距离适宜性地图对最终结果具有 50% (0.5) 的影响力,而到现有学校的距离则具有 25% (0.25) 的影响力。 坡度和土地利用类型均具有 12.5% (0.125) 的影响力。 与指定适宜性范围一样,指定权重也是一个主观的过程,因为这取决于哪些具体目标对于研究来说最重要。
最终的适宜性地图通过合并所有这些地图而生成。 可在合并各个适宜性地图的同时指定权重。 下方显示了用于选择建校地点的最终适宜性地图。 最适宜的地区以深绿色表示。 最不适宜的地区以红色暗影表示。
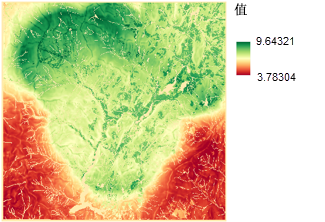
您可以使用地图代数对数据集进行加权及合并。 此外,也可以使用加权叠加或加权总和工具。 如果在模型中使用此工具,您便可以返回并轻松地更改权重(影响力百分比)和已设定的任何比例值。 如果您在模型中结合了地理处理工具,则只需创建一次模型,然后通过更改参数值便可体验不同的结果。
定位学校
此建模过程的最后一步是实际定位学校。 最终适宜性表面将相对于土地利用类型、坡度、到休闲娱乐场所的距离以及到学校的距离对每个地点的属性进行等级划分。 但是,拟建学校在空间上也有一定的要求,以确保其有效地发挥作用。
由于要容纳运动场,因此最佳建校地点的占地面积应为 150 英亩。 为了更加高效地建造和维护,场地的配置应相对紧凑。
将针对最终适宜性表面使用查找区域工具,以找到最佳的 150 英亩场地。
将拟建地点与上一步中的适宜性地图进行比较。
步骤 5:验证结果
通过空间分析得出结果后,应验证结果是否准确。 如有条件,应通过实地调查来验证候选地点是否符合要求。 通常,分析得出的结果尚未涵盖某些重要信息。 例如,该地点的上风向可能设有一个散发恶臭气味的养鸡场,或者通过查阅市政厅记录发现之前没有注意到在这块看中的土地上建造存在限制。 无论属于哪种情况,您都需要将这样的信息附加到分析中。
第 6 步:实施结果
空间建模的最后一步是实施结果,即在选好的地点着手规划和建造新学校。
有关适宜性建模的详细信息,请参阅了解适宜性建模工作流  应用分析主题。
应用分析主题。
参考资料
Malczewski, J. GIS and Multicriteria Decision Analysis. Wiley & Sons, 1999.