基于森林的预测的工作原理—ArcGIS Pro

基于森林的预测工具将使用基于森林的回归来预测时空立方体的未来时间片。主要输出是最终预测时间步长的地图以及信息性消息和弹出图表。可以提供其他解释变量来改进分析变量的预测，并且可以估算和可视化解释变量和被预测变量之间的滞后效应。您还可以选择在每个位置独立构建基于森林的模型、构建从所有位置训练的单个模型，或在每个时间序列聚类中构建单独的模型。此外，您还可以选择检测每个时间序列中的异常值，以识别与时间序列其余部分的模式和趋势显著不同的位置和时间。

当用于回归时，此工具将使用与基于森林的增强分类与回归工具相同的基础算法。系统将使用时空立方体每个变量上的时间窗来构造用于构建森林回归模型的训练数据。

了解有关基于森林的增强分类与回归的详细信息

可能的应用

森林回归模型很少对数据作出假设，因此在许多情况下都可以使用这种模型。当数据具有复杂的趋势或季节时，或数据以不同于常见数学函数（例如多项式、指数曲线或正弦波）的方式变化时，相比其他预测方法，该模型更为有效。

例如，您可以在以下应用程序中使用此工具：

学区可以使用此工具来预测该学区中每所学校在接下来的一周中每天缺席的学生人数。
州长可以预测未来两周因传染病住院的人数。该预测可以包括阳性检测结果的数量作为解释变量，并且该工具将对阳性检测和住院之间的滞后效应进行建模。
公共设施管理者可以使用此工具来预测其行政区域内的社区下个月的供电和供水需求。
零售店可以使用此工具来预测单个产品的售罄时间，以便更好地管理库存。
城市规划者可以使用此工具来预测未来人口，以便评估对住房、能源、食品和基础设施的需求。可以将规模和人口趋势相似的城市分组到一个聚类中，并且可以为每个组构建基于森林的模型。

预测和验证

该工具在预测每个时间序列时均会构建两个模型。第一个是预测模型，用于预测未来时间步长的值。第二个是验证模型，用于验证预测值。

注：

本部分将介绍模型比例参数的单个位置选项。整个立方体与时间序列聚类选项的操作方式类似。有关详细信息，请参阅扩展模型比例。

预测模型

预测模型将通过构建具有时空立方体每个位置的时间序列值的森林来进行构造。随后即可将该森林用于预测下一个时间片。系统会将新时间步长的预测值包括在森林模型中，然后预测下一个时间步长。此递归过程将针对所有未来时间步长继续进行。森林对每个时间序列的拟合度均会通过预测均方根误差 (RMSE) 进行测量，该均方根误差等于森林模型与时间序列值之间的均方差的平方根。

，其中 T 为时间步长数，c_t 为森林模型的值，而 r_t 为时间 t 处时间序列的原始值。

下图显示了时间序列的原始值和拟合至该时间序列的森林模型，以及对两个未来时间步长的预测。预测 RMSE 将测量森林中的拟合值与原始时间序列值之间的差异程度。

预测 RMSE 仅会测量森林模型对原始时间序列值的拟合程度。它无法测量预测模型对未来值的实际预测程度。常见的情况是，森林模型会紧密拟合时间序列，但在外推时无法提供准确的预测。验证模型可解决此问题。

验证模型

验证模型用于确定预测模型对每个时间序列的未来值的预测程度。该模型需通过排除每个时间序列的部分最终时间步长并将森林模型拟合到未排除的数据来进行构造。随后即可将该森林模型用于预测所保留数据的值，并将预测值与隐藏的原始值进行比较。默认情况下，系统将保留 10％的时间步长用于验证，但是可以使用为进行验证排除的时间步长数参数来更改此数字。所排除的时间步长数不能超过时间步长数的 25％，且如果将其指定为 0，则系统将不执行任何验证。预测的精度需通过计算验证 RMSE 统计数据来进行测量，该统计数据等于所排除时间步长的预测值与原始值之间的均方差的平方根。

，其中 T 为时间步长数，m 是为验证保留的时间步长数，c_t 为根据前 T-m 个时间步长预测的值，而 r_t 是为在时间 t 处验证保留的时间序列的原始值。

下图显示了拟合至时间序列前半部分，然后用于预测时间序列后半部分的森林模型。验证 RMSE 将测量所保留时间步长处的预测值与原始值之间的差异程度。

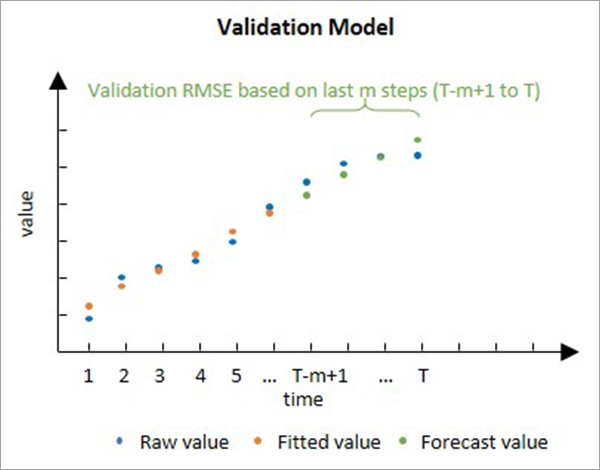
验证模型十分重要，因为它可以直接将预测值与原始值进行比较，以衡量森林的预测能力。尽管它实际上并不用于预测，但可将其用于证明预测模型的合理性。

注：

时间序列预测中的验证与名为交叉验证的常用技术相似但不相同。两者的不同之处在于，预测验证始终排除用于验证的最终时间步长，而交叉验证要么排除数据的随机子集，要么按顺序排除每个值。

解释

在解释“预测 RMSE”和“验证 RMSE”值时，需要牢记一些注意事项。

RMSE 值之间无法直接进行比较，因为它们测量的是不同的事物。预测 RMSE 测量的是森林模型对原始时间序列值的拟合度，而验证 RMSE 测量的是森林模型对未来值的预测能力。因为“预测 RMSE”使用的数据更多且不进行外推，所以它通常比“验证 RMSE”要小。
两种 RMSE 值均采用数据的单位。例如，如果您的数据是以摄氏度为单位的温度测量值，则验证 RMSE 50 将是非常高的值，因为这意味着预测值与真值平均相差大约 50 度。但是，如果您的数据是一家大型零售商店的日收入（以美元为单位），则相同的验证 RMSE 50 将会是很小的值，因为这意味着所预测日收入平均每天与真值的差仅为 50 美元。

构建和训练森林模型

要预测未来值，必须通过将解释变量与每个位置的因变量相关联来训练森林模型。森林模型需要重复的训练数据，但针对每个位置只有一个时间序列。要在单个时间序列中创建多组解释变量和因变量，系统需要构造时间窗，其中每个时间窗内的时间步长均用作解释变量，且时间窗之后的下一个时间步长将为因变量。例如，如果某个位置处有 20 个时间步长，而时间窗为 4 个时间步长，则系统会使用 16 组解释变量和因变量在该位置训练森林。第一组会将时间步长 1、2、3 和 4 作为解释变量，并将时间步长 5 作为因变量。第二组会将时间步长 2、3、4 和 5 作为解释变量，并将时间步长 6 作为因变量。最后一组会将时间步长 16、17、18 和 19 作为解释变量，并将时间步长 20 作为因变量。可以使用时间步长窗口参数来指定每个时间窗内的时间步长数。时间窗可以小到 1（从而使每个时间窗内只有一个时间步长），且不能超过该位置时间步长数的三分之一。

使用训练森林模型时，该位置的最终时间步长将用作解释变量，以预测第一个未来时间步长。随后，系统将使用时间窗中先前的时间步长来预测第二个未来时间步长，这些先前时间步长中有一个将是第一个预测值。第三个预测时间步长同样使用窗口中先前的时间步长，其中有两个时间步长是先前的预测时间步长。此过程将针对所有未来时间步长继续进行。

下图显示了用于训练森林模型和预测前七个未来时间步长的解释变量和因变量集：

扩展模型比例

除了在每个位置构建单独的预测模型之外，您还可以将位置分组到一起并构建一个可供组中所有位置使用的单一预测模型。您可通过对位置进行分组来执行不同比例的分析，例如按总人口规模分组的城市人口模型。您还可以使用同一组中的所有位置来构建全局模型。

当分组到一起时，所共享的预测模型将使用组中每个位置的时间窗作为训练数据，因此与任何单个位置相比，该方法都将具有更多可用于学习时间序列模式和趋势的数据。这一点对于每个时间序列中可用训练数据有限的短时间序列而言尤其重要。当组中的所有时间序列具有相似的值和模式时，这些额外的训练数据即可通过整合其他位置的模式来更为准确地对组中的每个位置进行预测。但是，如果组中位置的时间序列具有明显不同的值和模式，则整合它们的模式将会降低预测的准确性，因此仅对相似的时间序列进行分组十分重要。

您可以使用模型比例参数来定义分析比例。默认的单个位置选项将在每个位置构建独立模型以进行局部比例下的分析。整个立方体选项将使用所有位置来构建单个模型以进行全球比例下的分析。时间序列聚类选项将为时间序列聚类结果的每个聚类构建模型，以进行聚类比例下的分析（如果聚类形成了区域，则为区域比例的分析）。系统将在聚类变量参数中提供包含时间序列聚类结果的变量。

下图显示了为具有七个位置的整个立方体构建单个模型的示例：

下图显示了为两个时间序列聚类中的每一个构建单独模型的示例：

包括其他变量和滞后效应

森林回归模型不仅可以有效地捕捉时间序列的复杂模式和趋势，其还可以通过包括来自其他相关变量的附加信息来进行改进。例如，了解污染水平有助于预测因哮喘引起的急诊就诊次数，因为污染是已知的哮喘发作诱因。

您可以使用其他变量参数包括存储在同一时空立方体中的相关变量，以使用基于森林的多变量预测来预测分析变量。要训练多元森林回归模型，各其他变量均包含在各个时间窗内，并用于预测时间窗之后的下一个值，类似于时间窗如何用于分析变量，如构建和训练森林模型部分中所述。

当预测到新的时间步长时，每个相关变量都使用基于森林的一元预测进行预测，这些预测值在预测分析变量的未来值时将被用作解释变量。所有预测的结果（分析变量和所有解释变量）都存储在输出时空立方体中。

使用时间窗的多元预测

系统将使用时间窗创建多元预测。

您还可以使用基于森林的预测工具来估计和可视化分析变量与其他变量之间的滞后效应。滞后效应是指其他变量的变化与分析变量的变化之间存在延迟，在很多涉及多变量时间序列的情况下都存在滞后效应。例如，广告支出通常对销售收入具有滞后效应，因为人们在决定购买之前需要时间来查看广告在前面针对急诊室哮喘就诊次数和污染水平示例中，污染水平的上升与急诊室就诊次数的增加之间也可能存在滞后，因为负面健康影响可能需要一段时间才能累积到足以需要紧急护理的程度.

下图显示了滞后效应，其中蓝色时间序列值的变化比橙色线滞后四天：

当任何解释变量和分析变量之间存在滞后时，可以通过滞后的长度及时回顾来获得有关分析变量的详细信息。例如，如果广告支出和销售收入之间存在两周的滞后，那么在预测指定日期的销售收入时，与过去几天的支出金额相比，查看两周前的广告支出会提供更多信息。

森林模型可以检测和使用变量之间的滞后效应，因为移动时间窗总是预测紧随其后的时间步长。时间窗中的最后一个值总是比预测早一个时间步长；时间窗中最后一个时间补偿的下一个时间步长总是比预测早两个时间步长；等等。由于时间窗会发生变化，因此每个解释变量都表示为时间窗内每个时间步长的单独因素，从而可以比较不同滞后的不同解释变量，并确定哪些对预测最重要。有关详细信息，请参阅基于森林的增强分类与回归的工作原理。

例如，下图显示了 2021 年初预测 2019 年冠状病毒病 (COVID-19) 每日新增死亡人数的每个县的重要时间滞后变量。该模型使用每天接种疫苗的人数作为解释变量。 x 轴的值指的是时间窗内的每个时间步长，该图像有 14 个值，因为它使用了为期 14 天的时间窗。 x 轴的值表示预测前的时间步长数，因此当您在图表中从左向右移动时，它们会回到过去。最左边的值 1 表示它是预测前一天，对应于时间窗中的最后一个时间步长。同样，最右边的值 14 表示预测前 14 天，对应于 14 天时间窗的第一个时间步长。对于每个时间步长，浅蓝色和深蓝色列表示该因素被确定为预测 COVID-19 每日新增死亡人数的最重要因素之一的位置计数，因此计数越大，该系数的整体位置重要性越高。深蓝色条柱表示分析变量，COVID-19 新死亡人数，条柱在前三到四天的时间滞后中最高，表明前三到四天的死亡人数最能预测下一天的死亡人数。虽然此数据并未证明这一点，但变量本身可能会滞后，例如温度等周期性变量，由于昼夜循环，回顾 24 小时比回顾 2 小时更具预测性。浅蓝色条柱表示当天接种的新疫苗数量，最高的浅蓝色条柱出现在时间窗的 10 至 14 天前（最靠右的条），表明疫苗数量的增加或减少会影响未来 10 至 14 天的死亡人数。这 10 到 14 天的滞后对应于接种疫苗后产生峰值免疫力所需的时间。

时间滞后重要性图表包含在由可选输出重要性表参数生成的输出表中。

对于单个位置模型比例，该表将为每个位置的每个重要变量包含一个对应的行。在每个位置被视为重要的因素数量取决于重要性阈值参数值。例如，如果提供 15，则每个位置的前 15% 的因素将包含在表格和图表中。默认值为 10。要创建表格和图表，您必须在其他变量参数中至少包含一个其他变量。表格和图表中的时间滞后数等于时间步长窗口参数的值，因此时间窗必须比要捕获的任何滞后效应更宽。例如，一周的时间窗将无法捕捉疫苗对 COVID-19 死亡人数的滞后影响。

对于整个立方体模型比例，不需要提供其他变量来创建表格和图表，并且图表的 y 轴为原始重要性百分比（而非超过阈值的位置计数），原因是所有位置将共享相同的预测模型。下图显示了具有十二个时间滞后和三个变量的整个立方体分析的时间滞后重要性图表：

对于时间序列聚类模型比例，系统仅会在未提供其他变量的情况下创建图表，并且图表将显示按聚类分隔的图表格网。下图显示了三个时间序列聚类的时间滞后重要性：

低变异性的校正

如果某个位置的分析中使用的任何变量没有足够的可变性，则无法在该位置训练和估计基于森林的预测模型。如果一个位置的每个时间步长的分析变量都是常数，则该位置将被排除在训练之外；将在未来的每个时间步长中均预测常数值，并且预测中不包括置信区间。

如果该位置在时间序列中至少有两个唯一值，则会对分析变量和任何其他变量执行两次额外检查。首先，对于时间序列中的所有时间步长，确定包含常数值的比例。其次，仅对于未排除验证的时间步长，确定包含常数值的比例。如果这些比例中的任何一个超过三分之二，则会将少量随机噪声添加到值中以创建时间序列的可变性，并使用新值计算预测和验证模型。添加到每个时间步长的噪声是 0 到 0.000001 (1e-6) 之间的随机统一数值。如果时间序列值的范围小于 0.001，则噪声在 0 和范围值乘以 1e-6 之间是统一的。

即使添加了随机噪声，基于森林的模型仍然有可能在尝试 30 次后无法计算。这对于非常短的时间序列最常见。

季节性和选择时间窗

对森林模型而言，每个时间步长窗口内的时间步长数都是一个重要的选择。其中一个主要的考虑因素就是时间序列是否能够显示季节性（自然周期性模式针对一定数量的时间步长重复）。例如，温度将根据一年中的季节显示每年的季节周期。因为时间窗用于构建相关的解释变量和因变量，所以当这些解释变量全部来自同一季节周期时，最有效的做法是尽可能地缩小解释变量之间的季节相关性。建议您将自然季节中的时间步长数用于时间步长窗口的长度。如果您的数据可显示多个季节，建议您使用最长季节的长度。

如果您知道数据中与一个季节相对应的时间步长数，则可以在时间步长窗口参数中将其指定，随后该值将会被时空立方体中的每个位置使用。如果您不知道季节的长度，或如果不同位置的季节长度不同，则可以将该参数值留空，并使用频谱密度函数为每个位置估计最佳季节长度。有关此函数的详细信息，请参阅其他资源部分。

对于单个位置，如果通过频谱分析确定的最佳季节长度大于一且不大于该位置处时间步长数的三分之一，则时间步长窗口将被设置为该最佳值。否则，该位置将为时间步长窗口使用该位置处时间步长数的 25％（向下舍入）。这将确保窗口中至少有一个时间步长，且至少使用三个完整季节周期作为解释变量。该位置处使用的时间步长值将保存在输出要素的 Time Window 字段中。如果使用频谱分析确定了时间步长窗口，则输出要素的 Is Seasonal 字段将包含值 1，否则将包含 0。下图是对此工作流的汇总：

确定“时间步长窗口”参数 — 通过检测季节性，可以为每个位置指定或估计时间步长窗口。

对于整个立方体和时间序列聚类模型比例，默认时间窗为时间步长数的 25%（向下舍入）。这是因为不同的位置通常具有不同的季节性行为（例如，某些位置的冬季要比其他位置更早开始），所以无法估计单个季节性趋势并在组中的所有位置之间进行共享。

预测方法

您可使用四种方法来表示将用于训练森林的解释变量和因变量的值。这些选项将使用预测方法参数进行指定。

第一个选项是按值构建模型。此选项会将时空立方图格中的原始值用于解释变量和因变量。选择此选项后，预测值将包含在因变量的范围内，因此如果您预计数据中存在预测未来时该值将继续增加或减少的趋势，则不应使用此选项。下图显示了用于针对单个位置训练模型的变量集，其中的每一行都将显示解释变量集和相关的因变量。 T 为时空立方体中的时间步长数，W 为每个时间步长窗口中的时间步长数，而 X_t 为时间 t 处时间序列的原始值。

注：

对于整个立方体和时间序列聚类模型比例，按值构建模型是唯一可用的预测方法。

第二个选项是去除趋势后按值构建模型。此为工具的默认选项。此选项将针对每个位置处的整个时间序列执行一阶（线性）趋势移除，并将这些去趋势值用作解释变量和因变量。使用此选项可以使预测按照该趋势估计未来情况，从而可以在因变量范围之外估计预测值。下图显示了用于针对单个位置训练模型的变量集，其中的每一行都将显示解释变量集和相关的因变量。 T 为时空立方体中的时间步长数，W 为每个时间步长窗口中的时间步长数，而 D_t 为时间 t 处时间序列的去趋势值。

第三个选项是按残差构建模型。此选项将创建普通最小二乘法 (OLS) 回归模型，以基于每个时间窗内的解释变量来预测因变量。该回归模型的残差（OLS 预测与因变量原始值之间的差）用于表示训练森林时的因变量。下图显示了用于针对单个位置训练模型的变量集，其中的每一行都将显示解释变量集和相关的因变量。 T 为时空立方体中的时间步长数，W 为每个时间步长窗口中的时间步长数，X_t 为时间 t 处的时间序列值，而 X^{^}_t (X_t-hat) 是在时间 t 处根据 OLS 估算出的值。

最后一个选项是去除趋势后按残差构建模型。此选项首先会针对某个位置处的整个时间序列执行一阶（线性）趋势移除。然后，该选项将构建 OLS 回归模型，以便根据每个时间窗内的去趋势解释变量来预测去趋势因变量。该回归模型的残差（OLS 预测与因变量去趋势值之间的差）用于表示训练森林时的因变量。下图显示了用于针对单个位置训练模型的变量集，其中的每一行都将显示解释变量集和相关的因变量。 T 为时空立方体中的时间步长数，W 为每个时间步长窗口中的时间步长数，D_t 为时间 t 处的时间序列去趋势值，而 D^{^}_t (D_t-hat) 是在时间 t 处根据 OLS 估算出的值。

构建置信区间

如果验证至少排除两个时间步长，则该工具将为每个预测时间步长计算 90％的置信区间，这些置信区间将作为字段显示在输出要素中，并显示在工具输出部分中将要描述的弹出图表中。该工具将构建置信区间，方法为估计每个预测值的标准误差，然后在每个预测值以上和以下 1.645 个标准误差处创建置信界限。

该工具将执行以下计算来估计标准误差：

使用大小为 T 的时间窗来计算提前一步预测的验证 RMSE，以预测验证排除的时间步长。提前一步验证 RMSE 只能使用未用于训练预测模型且在预测该时间窗之后至少有一个时间步长的时间窗来进行计算。第一个时间窗是已排除时间步长之前的最后 T 个时间步长，且它将预测第一个已排除时间步长。第二个时间窗是最后 (T-1) 个时间步长和第一个已排除时间步长（该值将返回并用于计算 RMSE），且它将预测第二个已排除时间步长。最终时间窗将使用先前的 T 个时间步长（返回至数据集）来预测最终已排除时间步长。对于单个位置模型比例，提前一步预测将使用 M 值来计算 RMSE，原因是系统将保留 M 个时间步长以用于验证。对于整个立方体或时间序列聚类模型比例，组中的每个位置都将为提前一步 RMSE 计算贡献 M 个值。
还将使用已排除时间步长内的时间窗来计算提前两步预测的验证 RMSE。每个时间窗都将使用步长 1 的预测值作为最终时间步长，以预测下一个已排除时间步长。对于提前两步预测，每个位置都将为提前两步 RMSE 计算贡献 (M-1) 个值。
计算提前 K 步预测的验证 RMSE（最多提前 K=M 步）。每个位置都将使用提前 (K-1) 步 RMSE 计算得出的预测值，并在 RMSE 计算中贡献 (M-K+1) 个值。最终提前 M 步 RMSE 计算将为每个位置使用一个值。
使用 log(K) 作为解释变量来拟合预测组（或单个位置）中位置的平均提前 K 步 RMSE 的回归模型。使用此模型来估计所有未来时间步长（所有 K 值）的标准误差，其中包括第一批 M 预测值。

下图说明了整个立方体分析的此过程，其中保留了三个时间步长 (M=3) 以用于验证，而时间窗为四个时间步长 (T=4)。

注：

在某些情况下，预测标准误差的回归模型的估计斜率或截距可能为负。如果估计截距为负，则模型将在没有截距的情况下拟合。如果斜率为负，则系统将使用保留的时间步长（单个位置、时间序列聚类或整个立方体）中的最大 RMSE 作为所有预测值的标准误差。

识别时间序列异常值

时间序列数据中的异常值是与时间序列中其他值的模式和趋势显著不同的值。例如，在假期前后的大量在线购物或暴雨期间的大量交通事故可能会被视为其时间序列中的异常值。简单数据输入错误（例如省略数字的小数）是异常值的另一个常见来源。确定时间序列预测中的异常值非常重要，因为异常值会影响用于预测未来值的预测模型，即使位置时间序列中的少量异常值也会大大降低预测的准确性和可靠性。具有异常值的位置，尤其是在时间序列开始或结束时出现异常值的位置，可能会产生误导性的预测，并且识别这些位置可以帮助您确定您应对每个位置的预测值有多大的信心。

异常值不是仅由其原始值确定，而是由其值与预测模型的拟合值相差多少来确定。这意味着，一个值是否被确定为异常值取决于上下文，并且取决于它的位置和时间。预测模型将基于整个时间序列定义期望值，而异常值是与该基准显著偏离的值。例如，考虑年平均温度的时间序列。由于过去几十年来平均温度升高，因此拟合的温度预测模型也将随着时间的推移而增加，以反映这种升高现象。这意味着，如果 2020 年的温度与 1950 年被视为典型且非异常值的温度值相同，则很可能被视为异常值。换句话说，按照 2020 年的标准，1950 年的典型温度将被视为非常低。

您可以选择在每个位置使用识别异常值参数来检测时间序列异常值。如果指定，则将对每个位置执行广义极值标准化偏差 (ESD) 测试，以测试时间序列异常值。可以使用置信度参数指定测试的置信度，默认情况下将使用 90% 的测试的置信度。广义 ESD 测试将在每个位置迭代测试单个异常值、两个异常值、三个异常值，依此类推，直到最大异常值数参数（默认为时间步长数的 5%，四舍五入），并且返回具有统计显著性数量的异常值。可以在输出要素的属性表中看到每个位置的异常值，而在下一部分中讨论的时间序列弹出图表中则可看到单个异常值。

了解有关时间序列分析中的异常值、广义 ESD 测试以及如何解释结果的详细信息

工具输出

此工具的主要输出为 2D 要素类，其中显示了使用存储为字段的所有其他时间步长的预测，按最终预测时间步长符号化的输入时空立方体中的每个位置。虽然会独立预测每个位置，并且未考虑空间关系，但是对于具有类似时间序列的区域，地图可能会显示空间模式。

弹出图表

使用浏览导航工具单击地图上的任何要素将在弹出窗口窗格中显示一个图表，其中显示了时空立方体的值、拟合的森林模型和预测值以及每个预测的 90％置信区间。时空立方体的值将显示为蓝色，并通过蓝线进行连接。拟合的值将显示为橙色，并通过橙色虚线进行连接。预测的值将显示为橙色，并通过表示森林模型预测的橙色实线进行连接。每个预测值周围都将绘制出浅红色的置信界限。可以将鼠标悬停在图表中的任何点上，以查看该点的日期和值。此外，如果您选择检测时间序列中的异常值，则所有异常值都会显示为紫色大圆点。

注：

将输出要素另存为 shapefile (.shp) 时，将不会创建弹出图表。此外，如果置信区间超出了图表范围，则图表上方将显示显示完整数据范围按钮，您可以通过该按钮来扩展图表范围以显示整个置信区间。

地理处理消息

此工具将提供许多消息，其中包含有关工具执行的信息。消息具有三个主要部分。

输入时空立方体详细信息部分将显示输入时空立方体的属性以及有关时间步长数、位置数和时空立方图格数的信息。在第一部分中显示的属性取决于最初创建立方体的方式，因此该信息因立方体的不同而有所不同。

分析详细信息部分将显示预测结果的属性，其中包括预测的时间步长数、针对验证排除的时间步长数、通过频谱分析检测到季节性的位置的百分比以及有关预测的时间步长的信息。如果没有为时间步长窗口参数提供值，则系统将显示所估计时间步长窗口的汇总统计数据，其中包括最小值、最大值、平均值、中值和标准差。

各位置的精度汇总部分将显示所有位置之间的“预测 RMSE”和“验证 RMSE”的汇总统计数据。对于每个值，将显示最小值、最大值、平均值、中值和标准差。

如果您选择使用使用异常值选项参数来检测时间序列异常值，则会显示时间序列异常值汇总部分。此部分显示的信息包括异常值的位置数量和百分比、最多异常值的时间步长，以及按位置和时间步长计算的异常值数量的汇总统计数据。

注：

在工具执行期间，地理处理消息将显示在地理处理窗格底部。可将鼠标悬停在进度条上、单击弹出按钮或展开地理处理窗格中的消息部分来访问消息。您还可以使用地理处理历史访问之前运行工具的消息。

输出要素的字段

除了对象 ID、几何字段以及包含弹出图表的字段之外，输出要素将具有以下字段：

位置 ID (LOCATION) - 时空立方体相应位置的位置 ID。
（时间步长）中（分析变量）的预测（FCAST_1、FCAST_2，依此类推）- 每个未来时间步长的预测值。字段别名将显示分析变量的名称以及预测的日期。将为每个预测的时间步长创建此类型的字段。
（时间步长）中（分析变量）的高区间（HIGH_1、HIGH_2，依此类推）- 每个未来时间步长预测值的 90％置信区间上限。字段别名将显示分析变量的名称以及预测的日期。将为每个预测的时间步长创建此类型的字段。
（时间步长）中（分析变量）的低区间（LOW_1、LOW_2，依此类推）- 每个未来时间步长预测值的 90％置信区间下限。字段别名将显示分析变量的名称以及预测的日期。将为每个预测的时间步长创建此类型的字段。
预测均方根误差 (F_RMSE) - 预测 RMSE。
验证均方根误差 (V_RMSE) - 验证 RMSE。如果未针对验证排除任何时间步长，则不会创建此字段。
时间窗 (TIMEWINDOW) - 在该位置使用的时间步长窗口。
为季节性 (IS_SEASON) - 布尔变量，用于指示该位置处的时间步长窗口是否由频谱密度确定。值 1 表示已通过频谱密度检测到季节性，值 0 则表示未检测到季节性。如果在时间窗参数中指定了一个值，则所有位置在此字段中的值均为 0。
预测方法 (METHOD) - 一个用于显示森林模型参数的文本字段，这些参数包括随机种子、树数量、采样大小、预测方法、时间步长窗口是由用户指定还是通过工具确定、任何其他变量，以及有关模型比例和聚类可变性的信息（如果适用）。此字段可用于重新生成结果，从而使您可以确定按位置评估预测工具中使用了哪些模型。
模型拟合异常值数 (N_OUTLIERS) - 在该位置的时间序列中检测到的异常值数。仅当您选择使用异常值选项参数检测异常值时，才会创建此字段。

输出时空立方体

如果指定输出时空立方体，则输出立方体将包含输入时空立方体中的所有原始值以及附加的预测值。这一新建的时空立方体可以使用在 2D 模式下显示时空立方体或在 3D 模式下显示时空立方体工具进行显示，也可以用作时空模式挖掘工具箱中工具的输入，例如新兴热点分析和时间序列聚类。

可以使用按位置评估预测工具来比较和合并多个预测的时空立方体。由此即可使用不同的预测工具和参数来创建多个预测立方体，并且该工具可以使用“预测 RMSE”或“验证 RMSE”为每个位置标识最佳预测。

最佳做法和限制

在决定此工具是否适合您的数据以及使用哪些参数时，请考虑以下因素：

与时间序列预测工具集中的其他预测工具相比，此工具更为复杂，但对数据作出的假设最少。对于形状和趋势复杂且难以用简单或平滑数学函数进行建模的时间序列，建议使用此工具。当不满足其他方法的假设条件时，也建议使用此工具。
该工具可用于探索不同的模型比例以及不同时间序列变量之间的交互。建议您使用不同的比例和其他变量来多次运行该工具，并使用按位置评估预测工具来确定每个位置的最佳预测。
确定为进行验证排除的时间步长数参数的值非常重要。排除的时间步长越多，则用于评估验证模型的时间步长越少。但是，如果排除的时间步长过少，则将使用少量数据来评估“验证 RMSE”，并且可能会产生误导。建议您排除尽可能多的时间步长，同时仍保持足够的时间步长来估计验证模型。此外，建议您针对验证至少保留与要预测的时间步长数量相同的时间步长（如果时空立方体具有足够的时间步长以允许执行此操作）。
此外，为预测值构建置信区间需要将回归函数拟合到保留以用于验证的时间步长。因为至少需要两个值才能拟合这个函数，所以必须保留至少两个时间步长以创建预测的置信区间。但是，如果保留时间步长数较大，则回归函数将会更精确（生成更为精确的置信区间）。如需获得最为精确的置信区间，建议您至少保留 10% 的时间步长默认值以进行验证。
当时间序列中多次重复相同值时，此工具可能会生成不稳定和不可靠的预测。重复相同值的常见来源为零膨胀，其中数据表示计数，且许多时间步长值均为 0。
如果您选择识别异常值，建议您为时间步长窗口参数提供一个值，而不是将该参数留空，并在每个位置估算一个不同的时间步长窗口。对于每个位置，森林模型使用第一个时间步窗中的时间步来训练预测模型，并且仅在剩余时间步中检测异常值。如果不同的位置排除了不同数量的时间步进行训练，则汇总统计数据（例如每个时间步或每个位置的平均、最小和最大异常值数）可能会产生误导。这些统计数据仅针对每个位置所包括的时间步长进行计算。

其他资源

有关森林模型的详细信息，请参阅以下参考：

Breiman, Leo. (2001). "Random Forests." Machine Learning 45 (1): 5-32. https://doi.org/10.1023/A:1010933404324.
Breiman, L., J.H. Friedman, R.A. Olshen, and C.J. Stone. (2017). Classification and regression trees. New York: Routledge. Chapter 4.

有关森林模型的其他资源和参考资料，请参阅基于森林的增强分类和回归的工作原理。

有关用于估计时间窗长度的频谱密度函数的详细信息，请参阅以下参考资料中的 findfrequency 函数：

Hyndman R, Athanasopoulos G, Bergmeir C, Caceres G, Chhay L, O'Hara-Wild M, Petropoulos F, Razbash S, Wang E, and Yasmeen F (2019). "Forecasting functions for time series and linear models." R package version 8.7,https://pkg.robjhyndman.com/forecast.
Hyndman RJ and Khandakar Y (2008). "Automatic time series forecasting: the forecast package for R." Journal of Statistical Software, 26(3), pp. 1-22. https://www.jstatsoft.org/article/view/v027i03.

有关包括解释变量和滞后效应的详细信息，请参阅以下参考资料：

Zheng, H., and Kusiak, A. (2009). "Prediction of Wind Farm Power Ramp Rates: A Data-Mining Approach."ASME. J. Sol. Energy Eng, 131(3): 031011. https://doi.org/10.1115/1.3142727.