克里金法的工作原理—ArcGIS Pro

需要 Spatial Analyst 许可。

需要 3D Analyst 许可。

克里金法是通过一组具有 z 值的分散点生成估计表面的高级地统计过程。与插值工具集中的其他插值方法不同，要有效使用克里金法工具，需要在选择生成输出表面的最佳估算方法之前、对 z 值所表示的现象的空间行为进行交互式调查。

什么是克里金法？

IDW（反距离权重法）和样条函数法插值工具被称为确定性插值方法，因为这些方法直接基于周围的测量值或确定生成表面的平滑度的指定数学公式。第二类插值方法由地统计方法组成，例如克里金法，它们基于包含自相关的统计模型 - 即测量点之间的统计关系。因此，地统计技术不仅能够生成预测表面，还可以提供预测的确定性或准确性的某种度量。

克里金法假设采样点之间的距离或方向反映了空间相关性，可以用来解释表面的变化。克里金法工具可将数学函数与指定数量的点或指定半径内的所有点进行拟合以确定每个位置的输出值。克里金法是一个多步骤的过程；它包括数据的探索性统计分析、变异函数建模、创建表面以及（可选）探索方差表面。如果已知数据中存在空间相关距离或方向偏差时，克里金法是最合适的。该方法通常用在土壤科学和地质中。

克里金法公式

克里金法与 IDW 类似，它对周围的测量值进行加权以得出未测量位置的预测。这两种插值器的常用公式均由数据的加权总和组成：

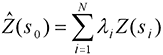
其中：
Z(s_i) = 第 i 个位置处的测量值
λ_i = 第 i 个位置处的测量值的未知权重
s0 = 预测位置
N = 测量值数

在反距离权重法中，权重 λ_i 仅取决于预测位置的距离。然而，克里金法的权重不仅基于测量点与预测位置之间的距离，还基于测量点的整体空间排列。为了在权重中使用空间排列，必须量化空间自相关性。因此，在普通克里金法中，权重 λ_i 取决于测量点、预测位置的距离和预测位置周围的测量值之间空间关系的拟合模型。以下部分将讨论如何使用常用克里金法公式创建预测表面地图和预测准确性地图。

使用克里金法创建预测表面地图

要使用克里金法插值方法进行预测，有两个任务是必需的：

找到依存规则。
进行预测。

要实现这两个任务，克里金法需要经历一个两步过程：

创建变异函数和协方差函数以估算取决于自相关模型（拟合模型）的统计相关性（称为空间自相关）值。
预测未知值（进行预测）。

由于这两个任务是不同的，因此可以确定克里金法使用了两次数据：第一次是估算数据的空间自相关，第二次是进行预测。

变异分析

拟合模型或空间建模也称为结构分析或变异分析。在测量点结构的空间建模中，以经验半变异函数的图形开始，针对以距离 h 分隔的所有位置对，通过以下方程进行计算：

半变异函数（距离 _h） = 0.5 * 平均值（（值 _i - 值 _j）²）

该公式涉及到计算配对位置的差值平方。

下图显示了一个点（红点）与所有其他测量位置的配对。会对每个测量点执行该过程。

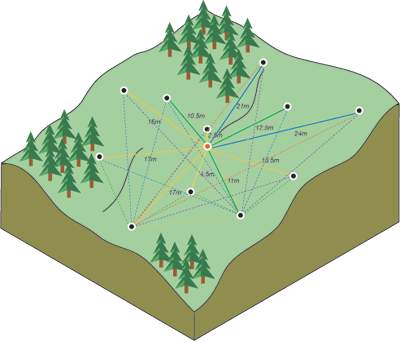
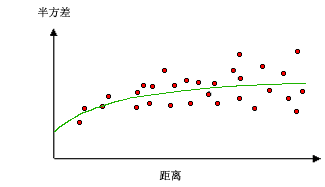
通常，每对位置都有唯一的距离，并且通常有很多对点。绘制所有对的图表很快就变得难以管理。所以，我们不再绘制每一对数据，而是将这些对数据分组到滞后区间中。例如，计算相距大于 40 米但小于 50 米的所有点对的平均半方差。经验半变异函数是 y 轴上表示平均半变异函数值，x 轴上表示距离或步长的图（请参阅下图）。

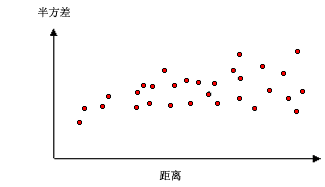
空间自相关对距离越近的事物就越相似这一基本地理原则进行量化。因此，较近的位置对（半变异函数云的 x 轴最左侧）应该具有更相似的值（半变异函数云的 y 轴较低位置）。位置对的距离变得越远（在半变异函数云的 x 轴上向右移动），就应该变得越不同，差值的平方就会更高（在半变异函数云的 y 轴上向上移动）。

根据经验半变异函数拟合模型

下一步是将模型拟合到形成经验半变异函数的点。半变异函数建模是空间描述和空间预测之间的关键步骤。克里金法的主要应用是预测未采样位置的属性值。经验半变异函数提供了有关数据集空间自相关的信息。但它并没有提供所有可能的方向和距离的信息。因此，为确保克里金法预测的克里金法方差为正值，根据经验半变异函数拟合模型（即连续函数或曲线）是很有必要的。该操作理论上类似于回归分析，在此回归分析中将根据数据点拟合连续线或曲线。

为了将模型拟合到经验半变异函数，请选择一个函数作为模型 - 例如，在超过一定范围的较大距离时上升并趋于平稳的球形类型（参见下面的球形模型示例）。经验半变异函数上的点与模型存在偏差；一些点位于模型曲线之上，一些点位于模型曲线之下。但是，如果将每个点在线上方的距离和每个点在线下方的距离相加，这两个值应该相似。有多种半变异函数模型可供选择。

半变异函数模型

克里金法工具提供了以下函数，可以从中选择用于经验半变异函数建模的函数：

圆形
球面
指数
高斯函数
线性函数

所选模型会影响未知值的预测，尤其是当原点附近的曲线形状明显不同时。接近原点处的曲线越陡，最接近的相邻元素对预测的影响就越大。因此，输出表面将不太光滑。每个模型都用于更准确地拟合不同种类的现象。

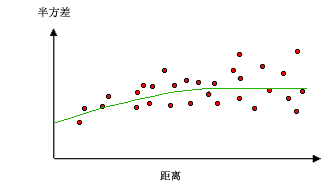
下图显示了两个常用模型并确定了函数的不同之处：

球面模型示例

该模型显示空间自相关性逐渐减少（相当于半方差增加），直到某个距离之外自相关性为零。球面模型是最常用的模型之一。

指数模型示例

当空间自相关性随着距离的增加而呈指数下降时适用此模型。在此，自相关只有在无限距离处才会完全消失。指数模型也是常用的模型。要选择使用哪个模型基于数据的空间自相关和数据现象的先验知识。

有关更多数学模型的信息，请参见下面。

了解半变异函数 - 变程、基台和块金

如前所述，半变异函数描述的是测量采样点的空间自相关性。根据地理学的基本原理（距离较近的事物更相似），距离较近的测量点的差值平方通常比较远的测量点的差值平方小。将每对位置分类后绘制出来后，就可以通过它们来拟合模型。通常使用变程、基台和块金描述这些模型。

变程和基台

当您查看半变异函数模型时，您会注意到在一定距离处模型会趋于平稳。模型首次变平的距离称为变程。距离比变程近的样本位置在空间上具有自相关性，而距离比变程远的样本位置则不具有自相关性。

半变异函数模型在变程值（y 轴上的值）处获得的值被称为基台值。偏基台等于基台减去块金。块金会在以下部分进行描述。

块金

从理论上讲，在零间距（例如，步长 = 0）处，半变异函数值是 0。但是，在无限小的间距处，半变异函数通常显示块金效应，即值大于 0。如果半变异函数模型在 2 处截取 y 轴，则块金值为 2。

块金效应常被视为测量误差，或距离小于采样间隔的空间变化源，或二者的组合。测量误差，由于测量设备固有的误差而产生。自然现象可以在一定尺度范围内发生空间变化。小于采样距离的微尺度变化将作为块金效应的一部分出现。收集数据之前，能够理解所关注的空间变化比例非常重要。

进行预测

找出数据中的相关性或自相关性（请参阅上面的变异分析部分）并完成首次数据应用后（即，使用数据中的空间信息计算距离和执行空间自相关建模），您可以使用拟合的模型进行预测。此后，将撇开经验半变异函数。

您现在可以使用数据进行预测。与 IDW 插值类似，克里金法根据周围的测量值形成权重来预测未测量的位置。与 IDW 插值一样，最接近未测量位置的测量值影响最大。然而，周围测量点的克里金法权重比 IDW 的权重更为复杂。 IDW 使用基于距离的简单算法，但克里金法权重来自于通过查看数据的空间特性而开发的半变异函数。要创建某现象的连续表面，将对研究区域（该区域基于半变异函数和附近测量值的空间排列）中的每个位置或单元中心进行预测。

克里金方法

存在两种克里金方法：普通克里金法和泛克里金法。

普通克里金法是最通用和最广泛使用的克里金方法，并且是默认克里金方法。该方法假设常量均值未知。如果不能拿出科学根据进行反驳，这就是一个合理假设。

泛克里金法假设数据中存在一个主导趋势（例如主导风向），并且可以用确定性函数（多项式）来建模。从原始测量点中减去该多项式，并根据随机误差对自相关进行建模。在模型适应随机误差之后且做出预测之前，多项式会被添加回预测中以给出有意义的结果。应该仅在您了解数据中存在某种趋势并能够提供科学判断描述泛克里金法时，才可使用该方法。

半变异函数图形

克里金法是一个复杂的过程，需要比本主题中提到的更多的空间统计知识。在使用克里金法之前，您应该彻底了解其基本原理，并评估您的数据是否适合使用该技术进行建模。如果没有充分理解该过程，强烈建议您查看本主题结尾列出的一些参考书目。

克里金法以区域化变量理论为基础，该理论假定 z 值所表示的现象的空间变化在整个表面中统计上是均匀的（例如，在表面上的所有位置都可以观察到相同的变化模式）。该空间一致性假设对于地区化的变量理论是十分重要的。

数学模型

下面是用于描述半方差的数学模型的常用形状和方程。

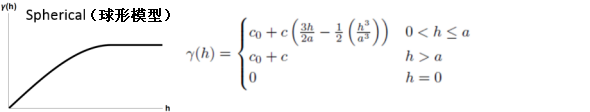
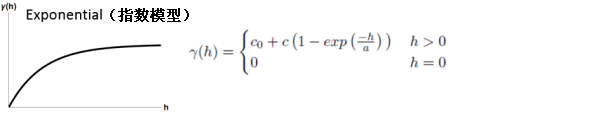
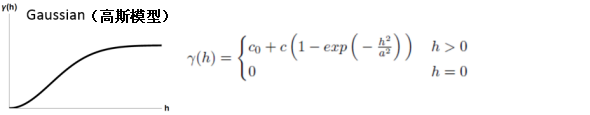
参考资料

Burrough, P. A. Principles of Geographical Information Systems for Land Resources Assessment. New York: Oxford University Press. 1986.

Heine, G. W. "A Controlled Study of Some Two-Dimensional Interpolation Methods." COGS Computer Contributions 3 (no. 2): 60–72. 1986.

McBratney, A. B., and R. Webster. "Choosing Functions for Semi-variograms of Soil Properties and Fitting Them to Sampling Estimates." Journal of Soil Science 37: 617–639. 1986.

Oliver, M. A. "Kriging: A Method of Interpolation for Geographical Information Systems." International Journal of Geographic Information Systems 4: 313–332. 1990.

Press, W. H., S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery. Numerical Recipes in C: The Art of Scientific Computing. New York: Cambridge University Press. 1988.

Royle, A. G., F. L. Clausen, and P. Frederiksen. "Practical Universal Kriging and Automatic Contouring." Geoprocessing 1: 377–394. 1981.