“多尺度表面百分位数”的工作原理

需要 Spatial Analyst 许可。

分析地形和其他表面是许多学科的重要组成部分，涵盖水文学到生态学等领域。 此类分析的结果通常取决于特定地形特征的数据或者计算的空间分辨率。 这种依赖性导致了多尺度分析方法的兴起，即对多个空间分辨率进行计算的分析。 这些多尺度方法可用于确定用于表征地形的最佳尺度，并测量参数对尺度变化的反应。

多尺度表面百分位数工具用于计算一系列空间尺度（大小不等的邻域）中的最极端百分位数。 距离 50 最远的百分位数（如接近 0 或 100 的值）将视为给定像元的最极端值。 此工具的输出用于识别像元的百分位数及发现其的尺度。

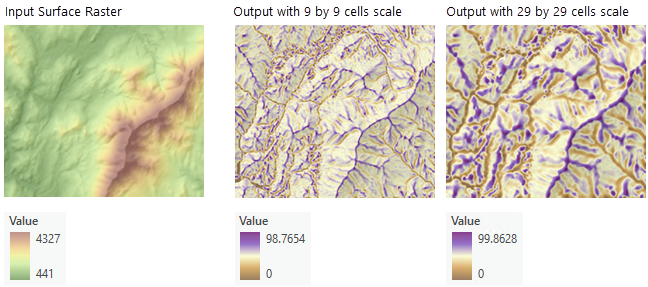
输出可用于解释输入表面栅格上的要素及其相关尺度。 以下示例显示了同一表面两种不同尺度的结果。 第一个图像（左）使用了 29 × 29 像元尺度，而第二个图像（右）使用了 49 × 49 像元尺度。 较小的尺度对景观的局部变化更为敏感，并能捕捉较小的表面要素。 另一方面，较大的尺度仅能捕捉较大的表面要素，因此显示的细节较少。

针对两个不同的尺度显示了相同范围的百分位数输出：较小尺度（第二张图）和较大尺度（第三张图）。

如何计算最极端的百分位数值

以下步骤概述了该工具使用的内部流程：

1. 可以使用最小邻域距离、最大邻域距离、基础距离增量和非线性因子参数定义分析的尺度。 这些参数的单位由距离单位参数控制。
2. 对于每个像元，将以每个识别的尺度计算百分位数。
3. 将针对各个尺度对计算的百分位数进行比较。 距离 50 最远的百分位数将视为给定像元的最极端百分位数。

下面的各部分将对每个步骤进行更详细的说明。

分析尺度的识别方式

将使用多尺度表面百分位数工具中的可选参数来确定分析尺度。 最小邻域距离和最大邻域距离参数用于设置分析的最小尺度和最大尺度。 基础距离增量和非线性因子参数用于控制最小值和最大值之间邻域距离的增加。

每个尺度用邻域距离值表示。 分析将在多个邻域距离下进行，具体取决于输入参数设置。

对于给定目标像元，将从目标像元中心向外测量邻域距离，由此在目标像元周围创建一个像元方块。 例如，对于像元大小为 10 米的输入表面栅格，如果邻域距离为 30 米，则将形成 7 x 7 像元的邻域，如下图所示。 此值（30 米）将为计算最极端百分位数的尺度之一。

将显示邻域距离（橙色线）和移动窗口的像素数之间的关系。 像元大小为 10 米时；10 米的邻域距离将使用 3 x 3 像元窗口（此为默认设置），20 米的邻域距离将使用 5 x 5 像元窗口，而 30 米的邻域距离将使用 7 x 7 像元窗口。

允许的最小邻域距离等于输入栅格的像元大小。 该值为 1 个像元，形成一个 3 x 3 的像元邻域。 在上述示例中，最小邻域距离为 5 米。

邻域距离不能超过输入表面栅格的范围。

如果指定的邻域距离不是像元大小的整数倍，工具会将其向上取整至下一个单元格大小的整数倍。 例如，在上述示例中，如果指定邻域距离为 25 米，它将向上取整至 30 米。

计算将从最小邻域距离参数值开始，然后计算每个后续邻域距离。

用于计算要使用的后续邻域距离的表达式如下：

ni = no + [Δn × (i - no)]p

• 其中：

  n_i = 步骤 i 的邻域距离

  n_o = 最小邻域距离

  Δn = 基础距离增量

  i = 正在计算邻域距离的步骤（其中第一步的值为 1 + n_o）

  p = 非线性因子

将检查识别的每个新邻域距离，以确定其是否小于或等于最大邻域距离参数值。 如果新距离值小于或等于最大值，则邻域距离计算将继续。 如果新值大于最大值，则表示已识别所有邻域距离，并且百分位数计算随即开始。

有关该部分分析的详细信息，请参阅以下如何计算百分位数部分。

非线性因子如何影响邻域距离

非线性因子参数用于控制邻域距离增加的栅格。 默认值为 1，这会导致邻域距离线性增加。 这意味着邻域距离之间的增量将等于基础距离增量参数值。

当将非线性因子参数值增大到 1 以上时，邻域距离之间的增量将在第一个增量之后发生变化。 第一个增量将等于基础距离增量值，但所有后续增量的大小将逐渐增大。

当将非线性因子参数值设置为 1 以上的值时，第一个增量之后的后续邻域距离之间的距离增量将逐渐增大。 另一个结果是，对于相同的最小和最大邻域值，较高的非线性因子将导致整体邻域距离较少。

下图演示了三种不同的非线性因子参数设置的影响。 在本示例中，设置为 1.0、1.5 和 2.0。 对于这些设置中的每种设置，其他参数的值均保持不变。 最小邻域距离参数值为 1，最大邻域距离值为 10，基础距离增量值为 1。

对于第一个增量，非线性因子的所有三个设置的邻域距离均为相同的值，即 2 个像元。 此后，邻域距离的值将开始变化。 当非线性因子为 1.5 时，增量将逐渐变大，当因子为 2.0 时，增量将更大。

当非线性因子参数值为 1.0 时，总共存在 9 个增量，每个增量将以线性方式大于前一个增量。 当因子值为 1.5 时，仅存在 4 个增量；当因子值为 2.0 时，仅存在 3 个增量。

将非线性因子增大到 1.0 以上会导致增量大小逐渐增大，因此邻域距离增加得更快。 这也会导致当使用较大的非线性因子值时，相同的“最小邻域距离”和“最大邻域距离”的尺度较小。

非线性因子参数用于自定义尺度的采样密度。 对于高程表面，高程百分位数在较小尺度上对邻域大小更敏感，在较大尺度上不太敏感。 使用大于 1.0 的非线性因子参数值，可以使小尺度的尺度采样密度更高，大尺度的尺度采样密度更低。 但是，在这些情况下，您可能需要增大最大邻域距离参数值，才能获得所需增量。 对于大多数情况，非线性因子使用 1.0 到 2.0 之间的值。

如何计算百分位数

百分位数是一种统计度量，用于指示数据集中低于给定值的值的百分比。 例如，对于 80 百分位数值，您将发现数据集中 80% 的值较低，而其余 20% 的值较高。

对于针对计算标识的每个邻域距离以及输入表面栅格中的每个像元，多尺度表面百分位数工具用于计算百分位数。 将在输出百分位数栅格参数值中标识并记录最极端的百分位数值。 确定这些百分位数的尺度将记录为输出尺度栅格参数值中的像元值。

用于计算每个像元处的百分位数的公式如下：

百分位数 = counti ∈C(zi < z0) × (100/nC)

• 其中：

  C = 针对处理确定的邻域

  count_{i ∈C} = 邻域 C 中的像元数量，其中 (z_i<z₀) 为 true

  z_i = 邻域 C 中像元 i 的值

  z₀ = 邻域 C 的中心像元的值

  n_C = 邻域 C 内包含的像元数量

下面显示了 3 x 3 像元邻域的计算示例。

该尺度为 3 x 3 像元，共存在 9 个像元。 在左侧，标识了处理像元的值和 8 个周围像元值（灰色）。 在右侧，显示了值小于中心像元的像元（绿色）以及等于或大于中心像元的像元（棕褐色）。

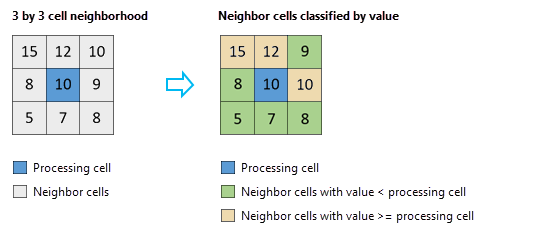
将上述公式应用于本示例将得到以下结果：

百分位数 = (像元值小于中心像元值的计数) * 100 / (邻域中像元的计数) = 5 * 100 / 9 = 55.5556

该方法利用 Huang 等人 (1979) 的运行直方图滤波算法，根据需要对百分位值进行分类。 找到百分位数值后，即可将该值与之前识别的最极端百分位数进行比较。 如果新值更极端，百分位数距离 50 更远，则将在输出百分位数栅格参数值中记录该位置的值。 将在输出尺度栅格参数值中记录尺度值。

GPU 的使用

如果您的系统上已安装某些 GPU 硬件，则此工具能够显著提高性能。 有关如何支持、配置以及启用此功能的详细信息，请参阅通过 Spatial Analyst 处理 GPU。

参考资料

Huang, Thomas S., G. Yang, and G. Tang. 1979. "A fast two-dimensional median filtering algorithm." IEEE Transactions on Acoustics, Speech, and Signal Processing Volume 27, Issue 1. pp.13–18. https://doi.org/10.1109/TASSP.1979.1163188

Newman, Daniel R., John B. Lindsay, and Jaclyn Mary Helen Cockburn. 2018. "Evaluating metrics of local topographic position for multiscale geomorphometric analysis." Geomorphology 312, 40–50. https://doi.org/10.1016/j.geomorph.2018.04.003