双变量空间关联 (Lee's L) 的工作原理

双变量空间关联 (Lee's L) 工具通过计算 Lee's L 统计量来评估两个连续变量之间的空间关联性（依赖性）。 该统计量衡量了变量之间的相关程度以及它们的共模式化（即空间聚集的相似性）。 Lee's L 统计量的取值范围在 -1 到 1 之间，类似于相关系数，但经过调整以考虑两个变量的空间自相关性。 Lee's L 值接近 1 表示变量高度正相关（当一个变量值较高时，另一个变量值也倾向于较高），并且两个变量都具有较强的空间自相关性（高值和低值分别倾向于聚集在一起）。 值接近 -1 表明变量高度负相关（当一个变量值较高时，另一个变量值倾向于较低），且同样具有较强的空间自相关性。 值接近 0 表明变量之间在空间上没有显著关联，意味着它们要么不相关，要么没有空间自相关性。 统计量还可以针对每个输入要素进行局部划分和分类，从而探讨分析变量在研究区域内的空间关联如何变化。

考虑变量的空间自相关性对于评估其空间关联性至关重要，因为传统的 Pearson 相关性检验在变量存在空间自相关时是无效的。 此外，传统检验无法评估两个变量的共模式化，而共模式化是变量之间空间关系的关键因素之一。

Lee's L 统计量的计算基于两个分析变量的局部邻域平均值的相关性，并通过对每个变量进行空间平滑调整来修正。 空间平滑系数的取值在 0 到 1 之间。 接近 1 的平滑系数表明强烈的空间自相关性（正或负），而接近 0 的系数表明这些值在空间上是随机的且没有自相关性。 较小的空间平滑系数会使 Lee's L 统计量相对于 Pearson 相关性有所减少，以反映变量缺乏空间聚集的情况。

下图展示了两个分析变量的不同地图示例，以及这些变量的 Pearson 相关系数和 Lee's L 统计量。 在每个图中，蓝色三角形的值为 1，橙色三角形的值为 0。

在第一个图中，两个分析变量在每个位置上的值完全相同，因此它们的 Pearson 相关系数为 1。 此外，这些变量各自具有很高的正空间自相关性，表明高值和低值分别聚集在一起。 这导致 Lee's L 统计量为 0.801，表明变量之间具有很高的正空间关联。

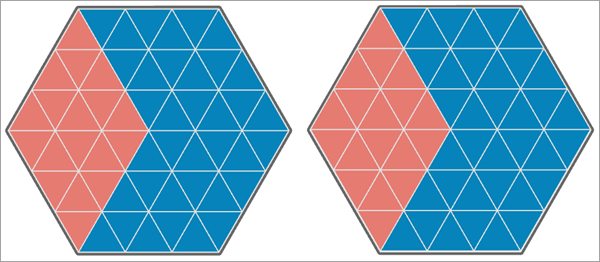
在第二个图中，第二个分析变量的值向右偏移了一个三角形，因此 54 个三角形中有 30 个值相匹配。 这导致 Pearson 相关系数为 0.167。 然而，由于每个变量的强空间自相关性，Lee's L 统计量略高，为 0.186。 这表明变量之间存在弱到中度的正空间关联。

在第三个图中，第二个分析变量的值移动到了六边形研究区域的另一侧，54 个三角形中有 18 个值匹配。 这导致 Pearson 相关系数为 -0.500，而 Lee's L 统计量为 -0.490，表明变量之间存在中到强的负空间关联。

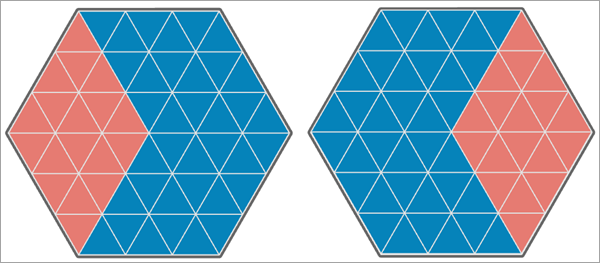
在最后一个图中，两个分析变量都具有负的空间自相关性，且没有一个三角形的值相同。 这导致 Pearson 相关系数为 -1，而 Lee's L 统计量为 -0.204，表明变量之间存在弱到中度的负空间关联。

局部 Lee's L 统计量

Lee's L 统计量可以细化到每个输入要素，用于观察变量之间的空间关联在空间和局部上的变化。 由于局部相关性和空间平滑的差异，某些区域或位置的空间关联可能会比整体（全局）Lee's L 统计量更高或更低。 通过直接比较局部 Lee's L 统计量与全局统计量的值，可以判断局部空间关联是否高于或低于全局水平。 与全局统计量不同，局部统计量的值可能超过 1 或低于 -1，且局部统计量的平均值总是等于全局统计量。

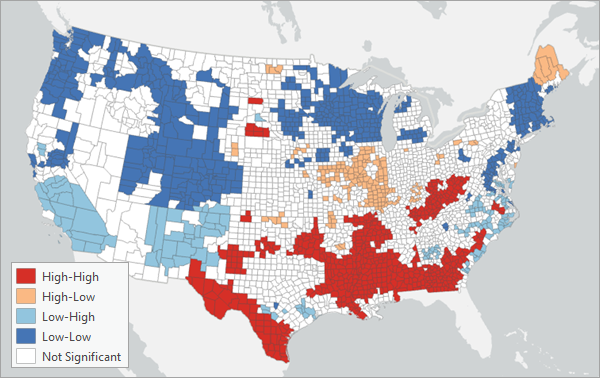
您还可以根据每个要素的统计显著性及其邻域的值，将局部 Lee's L 统计量分类为不同的类别。 每个要素可能有五种类别：Not Significant、High-High、High-Low、Low-High 和 Low-Low。 如果某个要素的局部 Lee's L 统计量没有达到至少 90% 的显著性水平，则它将被分类为“不显著”。 否则，如果第一个变量的邻域平均值高于该变量的整体平均值，且第二个变量的邻域平均值也高于该变量的整体平均值，则其将被分类为 High-High。 同样地，如果第一个变量的值低于平均值，而第二个变量的值高于平均值，它将被分类为 Low-High（反之亦然）。 区分这些类别非常重要，因为当两个变量在空间上正相关时，低值和高值分别倾向于聚集在一起。 这两种情况都会导致局部 Lee's L 统计量较大，因此这些类别能够明确指出每个要素的高关联性是由于两个变量都较高还是因为两个变量都较低。 对于负的空间关联，分类能够区分局部 Lee's L 统计量为负的原因是第一个变量较高而第二个变量较低，还是因为第一个变量较低而第二个变量较高。

在地图中运行时，输出图层将根据这五个类别进行绘制。 对于正空间关联的变量（全局 Lee's L 统计量大于 0），图层将主要包含 High-High 和 Low-Low 类别。 对于负空间关联的变量（全局 Lee's L 统计量小于 0），图层将主要包含 High-Low 和 Low-High 类别。

用例示例

您可以在以下场景中使用该工具：

• 调查大城市不同社区中教育水平与家庭收入之间的空间关联。 高教育水平的地区是否与高家庭收入的地区相关联？
• 研究植被覆盖率与空气质量之间的空间关系。 植被覆盖较多的区域是否倾向于拥有更好的空气质量？ 这种关系在统计上是否显著？
• 分析犯罪率与房产价值之间的关联。 在大都市的不同区域，这种关联是否会发生变化？

置换检验与 p 值

您可以通过置换检验来评估全局和局部 Lee's L 统计量的统计显著性。 置换检验是通过将两个分析变量的所有值随机重新分配到新位置（保持成对关系），然后计算重新分配后的全局和局部 Lee's L 统计量。 这个过程会重复多次（次数由置换次数参数决定），从而建立一个参考分布，并与原始的全局和局部 Lee's L 统计量进行比较。 如果原始统计量处于参考分布的极端位置（左侧或右侧），则意味着原始值很可能不是随机变化的结果，空间关联在统计上是显著的。 全局 Lee's L 统计量的 p 值将作为地理处理消息返回，而局部 Lee's L 统计量的 p 值及其显著性水平将作为输出要素类的字段返回。 有关详细信息，请参阅以下工具输出部分。

注：

p 值的计算方式为：统计比原始值更极端的置换值的数量，加上 1，再除以置换次数加 1。 这种调整确保了在样本较小时 p 值不会等于零。 随后，将该值乘以 2，获得双侧假设检验的 p 值。 检验的方向由极端值比例较小的一侧决定（即置换值大于或小于原始值的比例较小的一侧）。 需要注意的是，局部 Lee's L 统计量的 p 值未经过多重假设检验的调整，因此在解读局部 p 值时需要特别谨慎。

邻域类型

全局和局部 Lee's L 统计量的计算需要基于每个要素周围的邻域来估计空间关联性。 您可以通过邻域类型参数来指定每个要素的邻域。 参数包含的选项可用于定义哪些要素将被视为相邻要素。 无论选择哪种邻域类型，要素自身都会包含在其邻域中。

• 固定距离范围 - 将指定距离内的所有要素（最多 1,000 个要素）用作相邻要素。 默认距离为确保每个要素至少包含一个额外邻域的最短距离。 在距离范围参数中输入距离。 对于多边形，将使用中心点之间的距离来确定相邻要素。

  

• K 最近邻 - 将固定数量的最接近焦点要素的要素用作相邻要素。 在相邻要素的数目参数中提供值。 此值不包括焦点要素本身，因此实际参与计算的要素数比指定值多一个。 对于多边形，将使用中心点之间的距离来确定相邻要素。

  

• 仅邻接边 - 与焦点要素共享边的任何面都将用作相邻要素。 此选项仅适用于面要素。

  

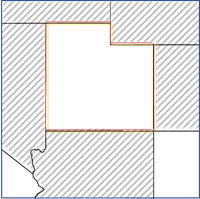
• 邻接边拐角 - 与焦点要素共享边或拐角的任何面都将用作相邻要素。 此选项仅适用于面要素。

  

• Delaunay 三角测量 - 通过在 Delaunay 三角测量（Thiessen 多边形）中共享边或角来确定相邻要素，并裁剪到点的凸包。 此选项仅适用于点要素。

  

• 通过文件获取空间权重 - 每个要素的相邻要素和权重由在权重矩阵文件参数中指定的空间权重矩阵文件定义。 可以使用生成空间权重矩阵或生成网络空间权重工具创建文件。

对于距离范围和相邻要素的数目类型的邻域，可以通过核函数对距离较近的邻居赋予更高的权重。 要对较近的相邻要素应用更大的权重，请在局部加权方案参数中选择二次函数选项。

双二次核函数使用以下公式定义权重：

核函数取决于控制权重随距离减少的速度的带宽。 每个核的带宽在核带宽参数中提供。 对于 K 最近邻邻域，如果未提供带宽值，每个要素将使用不同的自适应带宽，等于该要素到第 (k+1) 个相邻要素的距离。 对于距离范围邻域，默认核带宽为与距离范围参数相同的值。

注：

即使空间权重文件未分配这些权重，每个要素对其自身的权重也为 1。 此外，每个要素邻域的权重将被标准化为总和为 1（称为行标准化）。

工具输出

该工具会生成多种输出，您可以利用这些输出来分析两个分析变量之间的空间关联性。 结果会以地理处理消息、输出要素类和散点图的形式返回。

地理处理消息

地理处理消息中包含了与两个分析变量之间整体空间关联相关的值， 包括以下几项：

• 全局 Lee's L - 表示两个分析变量之间的 Lee's L 统计值。 该值介于 -1 和 1 之间。 正值表示正向空间关联，负值表示负向空间关联。 接近 0 的值表明变量在空间上无显著关联。 该统计量结合了分析变量邻域平均值的相关性以及每个变量的空间自相关性。
• 全局 p 值 - 用于检验空间关联是否具有统计显著性的双侧检验的 p 值。 较小的 p 值表明全局 Lee's L 统计量在统计上显著，不是随机变化的结果。 如果 p 值显著（90% 显著性水平为 0.1，95% 显著性水平为 0.05，99% 显著性水平为 0.01），且全局 Lee's L 统计量为正，表明两个分析变量在空间上显著正相关。 如果 p 值显著且全局 Lee's L 统计量为负，表明两个变量在空间上显著负相关。
• 空间平滑标量（分析字段 1）- 0 到 1 之间的值，用于指示第一个分析变量的空间自相关性。 接近 1 的值表示强正向空间自相关性（高值和低值各自倾向于聚集在一起），接近 0 的值表示强负向空间自相关性（高值和低值倾向于相互包围）。
• 空间平滑标量（分析字段 2）- 0 到 1 之间的值，用于指示第二个分析变量的空间自相关性。
• Pearson 相关性（原始数据） - 两个分析变量之间的 Pearson 相关性。 该值可用于与全局 Lee's L 统计量比较，查看变量的原始相关性与其空间关联之间的差异。
• Pearson 相关性（邻域平均值）- 两个分析变量的邻域加权平均值之间的 Pearson 相关性。 全局 Lee's L 统计量大致等于该值乘以空间平滑标量的平方根。

工具还将全局 Lee's L 统计量、全局 p 值和 Pearson 相关性（原始数据）作为派生输出返回。

要素类和字段

输出要素类将包含以下字段，汇总局部 Lee's L 统计量的结果：

• 两个分析变量的副本，以及每个输入要素的源 ID 字段。
• 局部空间关联 (LOCAL_L) - 每个要素的局部 Lee's L 统计量。 值大于 0 表示分析变量在该位置上有正向空间关联，值小于 0 表示有负向空间关联。
• 第一个分析变量的邻域加权平均值 (NWA_VAR1) - 每个要素的第一个分析变量的邻域加权平均值。 该值是使用邻域类型、局部加权方案和核带宽参数定义的权重计算出的要素及其相邻要素的加权平均值。
• 第二个分析变量的邻域加权平均值 (NWA_VAR2) - 每个要素的第二个分析变量的邻域加权平均值。
• p 值 (P_VALUE) - 用于检验每个要素的局部 Lee's L 统计量是否具有统计显著性的双侧检验 p 值。
• 显著性水平 (SIG_LEVEL) - 每个要素的局部 Lee's L 统计量的最高显著性水平。 可能的值为“不显著”、“90% 显著”、“95% 显著”和“99% 显著”。
• 局部空间关联类别 (ASSOC_CAT) - 每个要素的局部空间关联类别。 可能的值包括 Not Significant、High-High、High-Low、Low-High 和 Low-Low。 例如，Low-High 表示该要素的局部 Lee's L 统计量至少具有 90% 的显著性，第一个分析变量的邻域加权平均值低于其总体平均值，而第二个分析变量的邻域加权平均值高于其总体平均值。
• 相邻要素数 (NUM_NBRS) - 用于计算每个要素的全局和局部 Lee's L 统计量的邻居数量（包括该要素本身）。

Lee's L 散点图

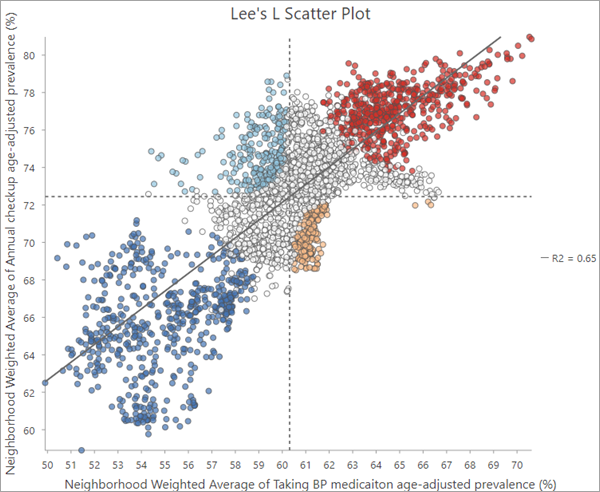
输出要素图层包含一个 Lee's L 散点图，显示第一个分析变量的邻域加权平均值在 x 轴上，第二个分析变量的邻域加权平均值在 y 轴上，并绘制一条线性趋势线。 虚线水平线和垂直线表示每个分析变量的平均值。 这些线将散点图分为四个象限，用于分类局部空间关联类别。 例如，左上象限中统计显著的要素将归入 Low-High（浅蓝色）类别。

该图还可以帮助识别偏离一般趋势的个别要素。 例如，您可以选择散点图中远离趋势线的点，进一步研究这些要素。 这些要素可能会在地图上聚集在一起，从而揭示出其他方法难以检测到的区域模式。

最佳做法和限制

使用此工具时应考虑以下问题：

• 在任一分析变量中，异常值（显著高于或低于其他值的值）可能会显著影响结果。 建议为每个分析变量绘制直方图，确定是否存在异常值，并移除包含异常值的要素。 您还可以使用数据工程工具识别异常值。
• 使用此工具时，假设两个分析变量的邻域加权平均值之间存在线性关系。 如果 Lee's L 散点图中的值显示出非线性模式，您可以使用变换字段工具对分析变量进行变换，线性化关系，然后使用转换后的值重新运行工具。
• 统计显著的 p 值（通常小于 0.05）并不一定意味着两个变量之间存在交叉相关性。 它可能仅仅表明其中一个或两个变量具有高空间自相关性。 要正确解读显著的 p 值，应结合全局 Lee's L 统计量、邻域平均值之间的相关性以及每个变量的空间平滑标量共同分析。 这些值可以帮助您判断统计显著性的来源：是自相关、交叉相关性，还是两者兼而有之。 如果 p 值显著，但全局 Lee's L 统计量和邻域平均值之间的相关性接近 0，且空间平滑标量接近 1，则可能意味着变量各自具有高度自相关性，但它们之间几乎没有交叉相关性。
• 建议至少使用 50 个输入要素，并为每个要素包含至少 8 个相邻要素。

公式

本部分提供了工具计算的所有统计量的公式。 有关推导和详细信息，请参阅下文参考部分的论文。

在所有公式中，x 表示第一个分析变量，y 表示第二个分析变量。 带有波浪号 (~) 的变量表示邻域值的加权平均值。 每个邻域的权重均已标准化为总和为 1。 带有横线的变量表示所有 n 个输入要素的未加权平均值。 下标 i 表示单个输入要素。 公式中的所有求和均为所有输入要素的求和。

全局 Lee's L 统计量计算公式如下：

全局 Lee's L 统计量大致等于空间平滑标量的平方根乘以邻域加权平均值之间的相关性，如下所示：

空间平滑标量的计算公式如下：

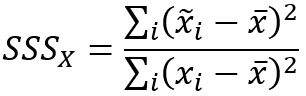
邻域加权平均值之间的相关性的计算公式如下：

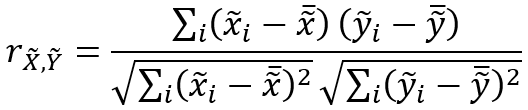
局部 Lee's L 统计量的计算公式如下：

全局 Lee's L 统计量等于局部 Lee's L 统计量的平均值，如下所示：

参考资料

使用了以下资源来实现该工具：

• Lee, Sang-Il. "Developing a bivariate spatial association measure: an integration of Pearson's r and Moran's I." Journal of geographical systems 3 (2001): 369-385. https://doi.org/10.1007/s101090100064.
• Lee, Sang-Il. "A generalized randomization approach to local measures of spatial association." Geographical Analysis 41.2 (2009): 221-248. https://doi.org/10.1111/j.1538-4632.2009.00749.x.