需要 Geostatistical Analyst 许可。
普通克里金法假设模型:
Z(s) = µ + ε(s)其中 µ 为已知常量。 关于普通克里金法的主要问题之一是常量均值的假设是否合理。 有时存在拒绝该假设的科学依据。 但是,作为一种简单的预测方法,它具有显著的灵活性。 下图是一个空间维度的示例:
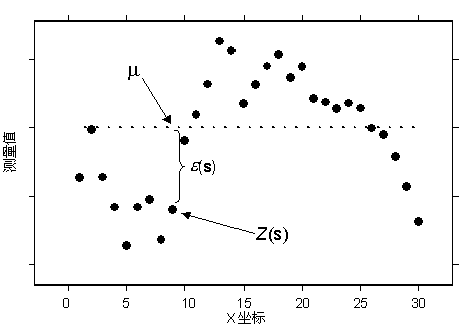
看起来数据是从穿过山谷和山脉的横断面采集的高程值。 此外,看起来左侧的数据变化更大,而右侧的数据变得更平滑。 事实上,通过具有恒定平均值 µ 的普通克里金模型模拟了此数据。 虚线给出了真实但未知的平均值。 因此,普通克里格法可用于似乎存在趋势的数据。 仅根据数据无法确定观察到的模式是自相关的结果(介于误差ε(s) 和 µ 常量之间),还是趋势(µ(s) 随 s 变化)的结果。
普通克里金法可以使用半变异函数或协方差(用于表达自相关的数学形式),可以使用变换并消除趋势,并允许测量误差。