需要 Geostatistical Analyst 许可。
三种克里金法(普通克里金法、简单克里金法和泛克里金法)均使用测量误差模型。 当同一位置可能存在多个不同的观测结果时,将会出现测量误差。 例如,可能需要从地面或空气中提取样本,然后将该样本划分为多个要进行测量的子样本。 如果用于测量样本的仪器存在一些变化,则可能需要执行此操作。 再举一例,您可能会将土壤样本的子样本送往不同的实验室进行分析。 此外,如果已记录仪器精度的变化,则可能也需要采取此类措施。 在这种情况下,您可能希望将已知测量变化输入到模型中。
测量误差模型
测量误差模型为
Z(s) = µ(s) + ε(s) + δ(s),其中 δ(s) 是测量误差,µ(s) 和 ε(s) 是平均值和随机变化。 在此模型中,块金效应由方差 ε(s)(称为微尺度变化)加上方差 δ(s)(称为测量误差)组成。 在 ArcGIS Geostatistical Analyst 扩展模块 中,可将估计的块金效应的比例指定为微尺度变化和测量变化,如果每个位置具有多个测量值,则需要 Geostatistical Analyst 估计测量误差,或者输入测量变化的值。 如果不存在测量误差,则克里金法是一种精确的插值器,这意味着:如果在已采集数据的位置进行预测,则预测值将与测量值相同。 但是,当存在测量误差时,您希望预测不具有测量误差项的过滤值 µ(s0) +ε(s0)。 在已采集数据的位置处,过滤值将与测量值不同。
在早期版本的 ArcGIS 中,默认测量变化为 0%,因此克里金法默认为精确的插值器。 在 ArcGIS 10 及更高版本中,默认测量变化设置为 100%,因此测量位置处的默认预测将基于数据的空间相关性以及附近位置的测量值。 测量误差可能由多种因素导致,其中包括测量设备、位置和数据集成的不确定性。 实际上,完全精确的数据极其罕见。
模型的效果
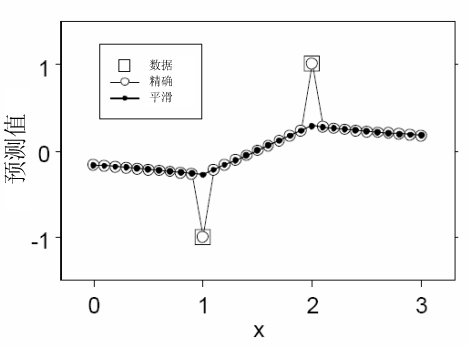
选择测量误差模型的效果是,最终的地图可以比精确的克里金法版本更平滑,并且标准误差更小。 下图通过示例对此进行了说明:当仅存在两个数据位置(分别位于 1 和 2 处,对应数值为 -1 和 1)时,针对无测量变化的模型和块金效应完全为测量变化的模型,显示了精确克里金法与平滑克里金法。