需要 Geostatistical Analyst 许可。
简单克里金法假设以下模型:
Z(s) = µ + ε(s)- 其中 µ 为已知常量
例如,下图使用与普通克里金法和泛克里金法概念相同的数据,观测数据由实心圆指示:
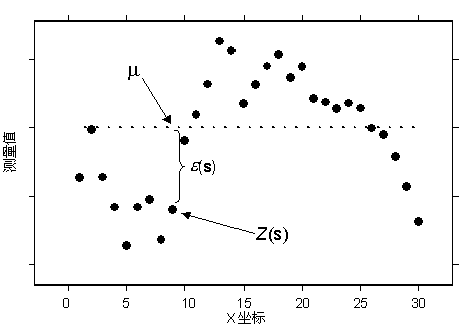
虚线表示的已知常量为 µ。可以与普通克里金法进行比较。 对于简单克里金法,由于假设 µ 完全已知,因此您也能准确地得出数据位置处的 ε(s)。 对于普通克里金法,由于已估算 µ,因此您也估算了 ε(s)。 如果已知 ε(s),则相比需要估算 ε(s) 的情况,可以更好地估算自相关性。 假设已知 µ 的确切平均值通常不现实。 但是,有时假设基于物理的模型能够提供已知趋势是合理的。 然后,即可获取该模型与观测值之间的差异(称为残差),并对残差使用简单克里金法,其中假设残差的趋势为零。
简单克里金法可以使用半变异函数或协方差(用于表达自相关的数学形式),可以使用变换,并允许测量误差。