Fonctionnement de l’outil Détection des points de changement

L’outil Détection des points de changement identifie, pour chaque emplacement d’un cube spatio-temporel, les intervalles temporels lorsqu’une propriété statistique de la série chronologique change. L’outil peut détecter des changements de la valeur moyenne, de l’écart type ou de la pente (tendance linéaire) de variables continues, ainsi que des changements de la moyenne des variables de total. Le nombre de points de changement à chaque emplacement peut être déterminé par l’outil ou un nombre défini de points de changement peut être spécifié et utilisé pour tous les emplacements.

Les points de changement divisent chaque série chronologique en segments dans lesquels les valeurs possèdent une moyenne, un écart type ou une tendance linéaire similaire (pente et intersection). Les points de changement étant définis comme constituant le premier intervalle temporel dans chaque nouveau segment commençant le deuxième segment, le nombre de points de changement est toujours inférieur de un par rapport au nombre de segments.

Types de points de changement

L’outil peut détecter quatre types de changement. Dans chaque image ci-dessous, la série chronologique est représentée par un diagramme linéaire bleu avec des lignes orange verticales aux points de changement.

• Mean shift (Décalage moyen) : détecte les décalages de la valeur moyenne de la variable d’analyse. Les valeurs de données sont censées suivre une distribution normale, tous les intervalles temporels ayant le même écart type. La valeur moyenne est constante au sein de chaque segment et prend une nouvelle valeur à chaque point de changement.

  

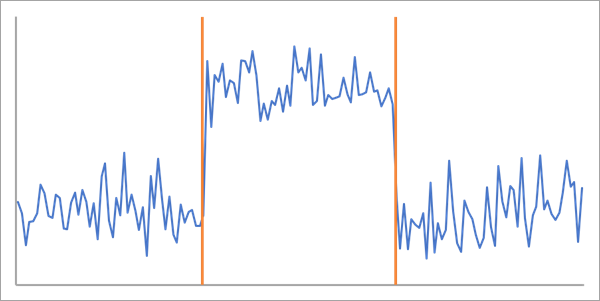
  • Application possible : détectez des vagues de chaleur lorsque la température maximale quotidienne augmente sur une courte période.
• Standard deviation (Écart type) : détecte les changements de l’écart type de la variable d’analyse. Les valeurs de données sont censées suivre une distribution normale, tous les intervalles temporels ayant la même valeur moyenne. L’écart type est constant au sein de chaque segment et prend une nouvelle valeur à chaque point de changement.

  

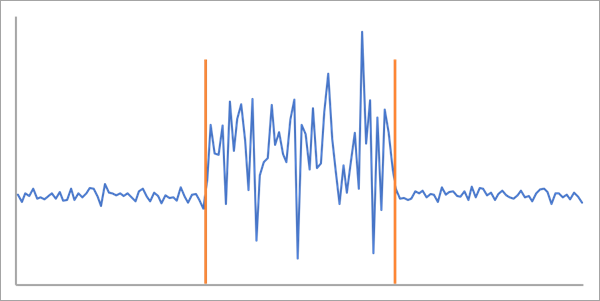
  • Application possible : détectez des changements dans la variation de la vitesse du vent susceptibles d’indiquer des phénomènes météorologiques sévères.
• Pente (tendance linéaire) : détecte les changements de tendance linéaire de la variable d’analyse. Les valeurs de données sont censées suivre une distribution normale, une valeur moyenne étant définie par une ligne et tous les intervalles temporels ayant le même écart type. La pente et l’intersection de la ligne sont constantes au sein de chaque segment et prennent une nouvelle valeur à chaque point de changement.

  

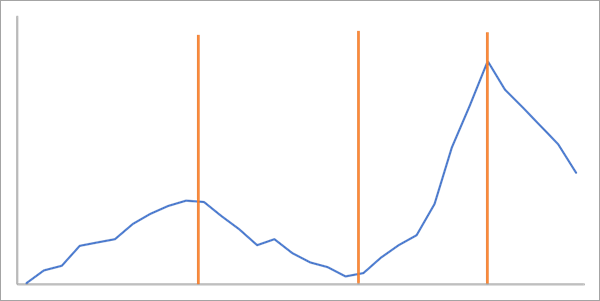
  • Application possible : détectez des changements de la tendance des recettes commerciales pour déterminer les campagnes marketing les plus efficaces.
• Count (Décompte) : détecte les changements de la valeur moyenne d’une variable d’analyse représentant des décomptes. Les valeurs de données sont censées suivre une distribution de Poisson au sein de chaque segment, avec une moyenne qui prend une nouvelle valeur à chaque point de changement.

  

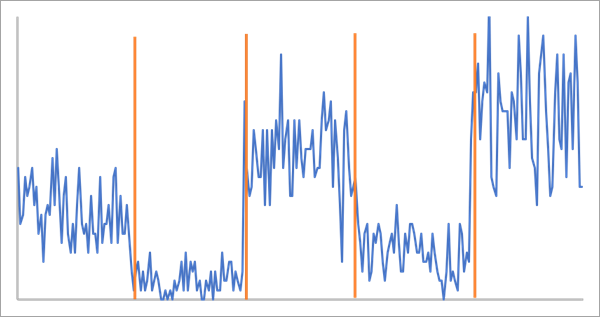
  • Application possible : détectez des changements dans les nombres de cas de grippe quotidiens pour estimer le début et la fin de chaque saison grippale.

Sorties de l'outil

La sortie principale de l’outil est constituée d’une classe d’entités comportant une entité pour chaque emplacement du cube spatio-temporel en entrée. La couche est affichée avec cinq classes basées sur le nombre de points de changement détectés à chaque emplacement.

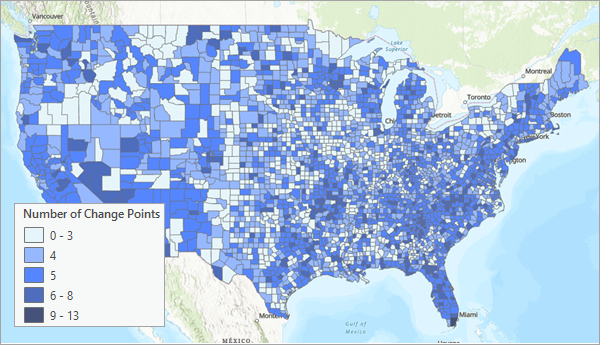
Les entités en sortie incluent les champs suivants :

• Number of Change Points (Nombre de points de changement) (NUM_CPTS) : nombre de points de changement détectés à l’emplacement.
• Date of First Change Point (Date du premier point de changement) (FIRST_CHPT) : date du premier point de changement à l’emplacement. Si aucun point de changement n’est détecté, la valeur est nulle.
• Date of Last Change Point (Date du dernier point de changement) (LAST_CHPT) : date du dernier point de changement à l’emplacement. Si aucun point de changement n’est détecté, la valeur est nulle. Si un point de changement est détecté, la valeur est identique à celle de la date du premier point de changement.

L’heure de la couche des entités en sortie étant basée sur la date du premier point de changement, vous pouvez utiliser le curseur temporel pour filtrer les emplacements en fonction de cette date. La propriété de date/heure de la couche peut être redéfinie sur la date du dernier point de changement dans les propriétés de la couche. Cela permet, par exemple, de créer une animation dans le temps pour visualiser quand différents emplacements connaissent leur premier ou leur dernier point de changement, afin d’identifier des modèles temporels sur plusieurs emplacements.

Diagrammes contextuels de série chronologique

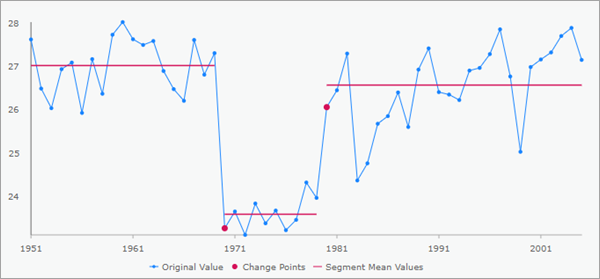
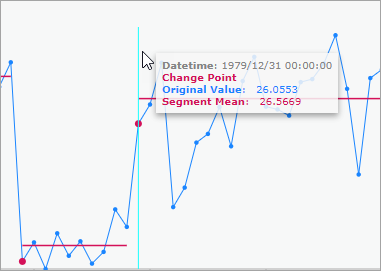
En cliquant sur n’importe quelle entité de la carte à l’aide de l’outil de navigation Explore (Explorer), un diagramme linéaire s’affiche dans la fenêtre Pop-up (Fenêtre contextuelle). Dans ce diagramme, la série chronologique à l’emplacement est représentée par un diagramme linéaire bleu et les points de changement sont indiqués par de gros points rouges.

Pour les types de changement Mean shift (Décalage moyen) et Count (Décompte), des lignes rouges horizontales sont tracées à la valeur moyenne de chaque segment.

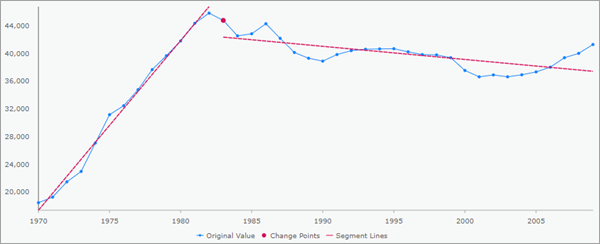
Pour les types de changement Pente (tendance linéaire), les lignes rouges sont tracées pour représenter la tendance linéaire de chaque segment.

Pour le type de changement Standard deviation (Écart type), une ligne pleine rouge est tracée à la valeur moyenne globale de la totalité de la série chronologique. Pour chaque segment, des lignes pointillées rouges sont tracées deux écarts types au-dessus et en dessous de la moyenne globale, l’espace entre ces bandes étant teinté en rose. Ces bandes rétrécissent ou s’élargissent lorsque l’écart type change aux points de changement. Des lignes pointillées grises sont tracées deux écarts types globaux au-dessus et en dessous de la moyenne globale. Cela vous permet de déterminer si l’écart type d’un segment est plus grand ou plus petit que l’écart type de la totalité de la série chronologique.

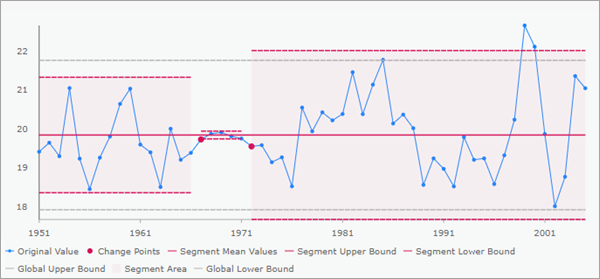
Vous pouvez placer le pointeur de la souris sur n’importe quel élément du diagramme pour afficher plus d’informations sur les valeurs.

Remarque :

Les diagrammes de fenêtre contextuelle ne sont pas créés lorsque les entités en sortie sont enregistrées en tant que shapefile (.shp).

Messages de géotraitement

L’outil fournit un certain nombre de messages d’informations sur l’exécution de l’outil. Les messages comportent différentes sections.

La section Input Space Time Cube Details (Détails du cube spatio-temporel en entrée) affiche les propriétés du cube spatio-temporel en entrée ainsi que des informations sur l’intervalle de pas de temps, le nombre de pas de temps, le nombre d’emplacements et le nombre de groupes spatio-temporels. Les propriétés affichées dans cette première section dépendent de la façon dont le cube a été créé, de sorte que les informations varient d’un cube à l’autre.

La section Important Dates (Dates importantes) affiche les dates du premier et du dernier point de changement de tous les emplacements, ainsi que la date comptabilisant le plus de points de changement. Vous pouvez l’utiliser pour identifier les dates où des changements importants se sont produits et ont provoqué des changements dans plusieurs emplacements. En cas d’égalité, la date la plus ancienne est affichée.

La section Summary of Number of Change Points Per Time Step (Résumé du nombre de points de changement par intervalle temporel) affiche le minimum, le maximum, la moyenne, la médiane et l’écart type du nombre de points de changement par intervalle temporel. Cela vous permet d’étudier la fréquence des points de changement sur la série chronologique à tous les emplacements. Si cette fréquence est trop élevée ou trop basse, vous pouvez ajuster la valeur du paramètre Detection Sensitivity (Sensibilité de la détection) pour augmenter ou diminuer la fréquence des points de changement.

Visualiser le cube spatio-temporel en 3D

Le cube spatio-temporel en entrée est mis à jour avec les résultats de l’analyse et peut être utilisé dans l’outil Visualiser le cube spatio-temporel en 3D avec l’option Time series change points (Points de changement dans une série chronologique) du paramètre Display Theme (Thème d’affichage) pour afficher les résultats dans une scène 3D. La sortie contient une entité par intervalle temporel du cube spatio-temporel. Les intervalles temporels détectés en tant que points de changement sont étiquetés Change Point (Point de changement) et s’affichent en violet, tandis que les intervalles temporels qui ne sont pas détectés en tant que points de changement sont étiquetés Not a Change Point (Pas un point de changement) et s’affichent en gris clair.

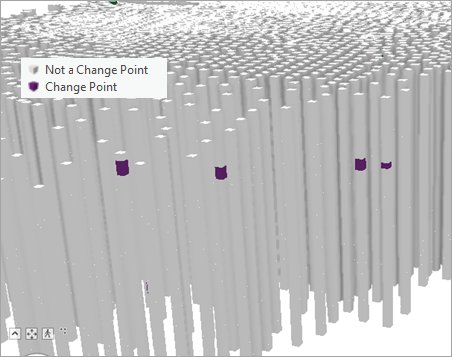
Les champs d’information relatifs à l’heure, à l’emplacement et à l’ID de l’intervalle temporel sont inclus avec les champs suivants relatifs aux points de changement détectés :

• Change Point Indicator (Indicateur de point de changement) (CHPT_IND) : ce champ contient la valeur 1 si l’intervalle temporel est détecté en tant que point de changement et 0 si l’intervalle temporel n’est pas détecté en tant que point de changement.
• Current Mean (Moyenne actuelle) (MEAN_CUR) : valeur moyenne du segment contenant l’intervalle temporel. Ce champ est créé uniquement pour le type de changement Décalage moyen.
• Mean Before (Moyenne avant) (MEAN_BEF) : valeur moyenne du segment contenant l’intervalle temporel précédent. Les valeurs Current Mean (Moyenne actuelle) et Mean Before (Moyenne avant) sont égales si l’intervalle temporel n’est pas un point de changement et sont différentes si l’intervalle temporel est un point de changement (étant donné que la valeur précédente se trouve dans un segment différent). Cela vous permet de comparer les valeurs moyennes des segments avant et après le point de changement. Ce champ est créé uniquement pour le type de changement Décalage moyen.
• Current Standard Deviation (Écart type actuel) (STDEV_CUR) : écart type du segment contenant l’intervalle temporel. Ce champ est créé uniquement pour le type de changement Écart type.
• Standard Deviation Before (Écart type avant) (STDEV_BEF) : écart type du segment contenant l’intervalle temporel précédent. Les valeurs Current Standard Deviation (Écart type actuel) et Standard Deviation Before (Écart type avant) sont égales si l’intervalle temporel n’est pas un point de changement et sont différentes si l’intervalle temporel est un point de changement. Ce champ est créé uniquement pour le type de changement Écart type.
• Current Mean of Counts (Moyenne actuelle des décomptes) (MEAN_CUR) : valeur moyenne des décomptes du segment contenant l’intervalle temporel. Ce champ est créé uniquement pour le type de changement Décompte.
• Mean of Counts Before (Moyenne des décomptes avant) (MEAN_BEF) : valeur moyenne des décomptes du segment contenant l’intervalle temporel précédent. Les valeurs Current Mean of Counts (Moyenne actuelle des décomptes) et Mean of Counts Before (Moyenne des décomptes avant) sont égales si l’intervalle temporel n’est pas un point de changement et sont différentes si l’intervalle temporel est un point de changement. Ce champ est créé uniquement pour le type de changement Décompte.
• Pente actuelle (SLOPE_CUR) : pente de la ligne du segment contenant l’intervalle temporel. Ce champ est créé uniquement pour le type de changement Pente (tendance linéaire).
• Pente avant (SLOPE_BEF) : pente de la ligne du segment contenant l’intervalle temporel précédent. Ce champ est créé uniquement pour le type de changement Pente (tendance linéaire).
• Intersection actuelle (INTRCP_CUR) : intersection de la ligne du segment contenant l’intervalle temporel. Ce champ est créé uniquement pour le type de changement Pente (tendance linéaire).
• Intersection avant (INTRCP_BEF) : intersection de la ligne du segment contenant l’intervalle temporel précédent. Ce champ est créé uniquement pour le type de changement Pente (tendance linéaire).

Remarque :

Le thème d’affichage Time series change points (Points de changement dans une série chronologique) de l’outil Visualiser le cube spatio-temporel en 2D recrée la classe d’entités requise en sortie de la détection des points de changement.

Fonctionnement de la détection des points de changement

L’objectif de la détection des points de changement est de trouver des intervalles temporels pour lesquels la valeur de la moyenne, de l’écart type ou de la pente des changements de données est remplacée par une autre. On rencontre la même difficulté qu’avec la segmentation de la série chronologique, où une série chronologique est divisée en segments dont les valeurs ont une moyenne, un écart type ou une pente similaire. Pour déterminer la segmentation (ensemble de points de changement) optimale d’une série chronologique donnée, vous devez pouvoir mesurer et comparer l’efficacité des différentes segmentations possibles. Cette comparaison nécessite de calculer le coût de chaque segmentation, celle dont le coût est le plus faible étant la plus adaptée.

Le coût d’une segmentation est calculé en additionnant les coûts individuels de chacun de ses segments. Le coût de chaque segment est basé sur une fonction de vraisemblance déterminée par le type de changement (voir les hypothèses de distribution de chaque type de changement dans la section Types de points de changement). Intuitivement, plus les segments suivent étroitement la distribution supposée du type de changement, plus la vraisemblance est forte et plus le coût de la segmentation est faible.

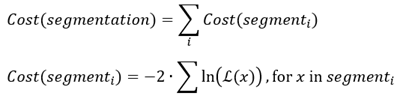
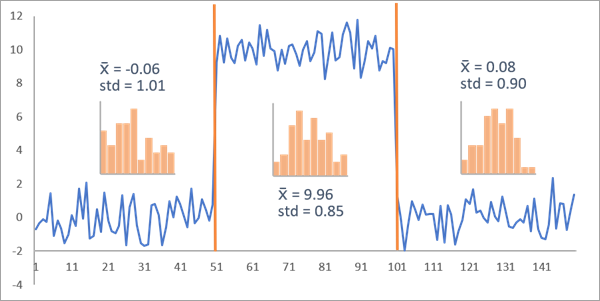
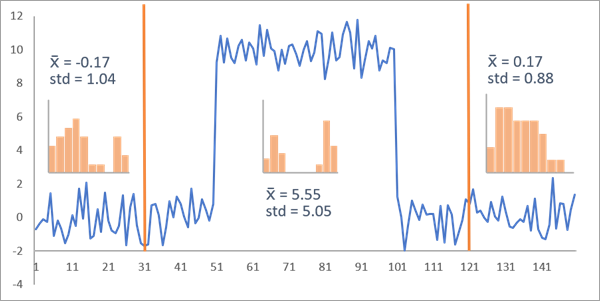
Par exemple, l’image ci-dessous présente une série chronologique comportant 150 intervalles temporels où toutes les valeurs ont été générées à partir d’une distribution normale avec un écart type égal à 1. La moyenne des 50 premiers intervalles temporels est égale à 0, puis elle augmente à 10 pour les 50 intervalles temporels intermédiaires, avant de redescendre à 0 pour les 50 derniers. Les points de changement étant définis comme les premiers intervalles temporels de chaque nouveau segment, dans cette série chronologique, les intervalles temporels 51 et 101 sont les véritables points de changement où la moyenne connaît un décalage. D’après leur histogramme individuel, chaque segment semble suivre une distribution normale, avec un écart type à peu près égal mais une valeur moyenne différente. Cette segmentation semble donc se conformer aux hypothèses du type de changement Décalage moyen. Cela signifie que la vraisemblance de cette segmentation est forte et que le coût de segmentation résultant est faible. Une segmentation correcte comme celle-ci représente un coût de 401,39 lors de la détection du décalage moyen. Cette valeur, difficile à comprendre seule, peut être comparée au coût d’autres segmentations possibles.

L’image ci-dessous représentent une segmentation incorrecte où les intervalles temporels 31 et 121 sont détectés en tant que points de changement. Dans le segment intermédiaire, la distribution ne semble pas être normale et l’écart type est beaucoup plus grand que dans les premier et dernier segments. Cela suggère que les valeurs de données des segments ne sont pas vraisemblables selon l’hypothèse de distribution du type de changement Décalage moyen et en conséquence, que le coût de la segmentation doit être élevé. En effet, cette segmentation représente un coût de 2 596,24, bien supérieur au coût de la segmentation correcte. Ceci confirme que ces points de changement ne sont pas optimaux pour cette série chronologique.

Supposons maintenant qu’un point de changement superflu est ajouté aux deux véritables points de changement. Dans l’image ci-dessous, les intervalles temporels 51, 101 et 131 sont identifiés en tant que points de changement. Même si le dernier point de changement est superflu, les histogrammes des segments semblent montrer que la distribution est normale avec un écart type à peu près égal, ce qui indique une forte vraisemblance et un faible coût de segmentation. Cette segmentation représente en effet un coût de 401,27, légèrement inférieur au coût de la segmentation véritable (401,39). Le coût de cette segmentation avec un point de changement inutile est plus faible que celui de la véritable segmentation parce que les vraisemblances ne diminuent jamais avec l’ajout de nouveaux paramètres (en l’occurrence, de nouveaux points de changement). Le point de changement supplémentaire ajouté n’a entraîné qu’une baisse légère du coût parce qu’il améliorait très peu l’adaptation du modèle aux données, par rapport au fait de ne pas l’inclure en tant que point de changement.

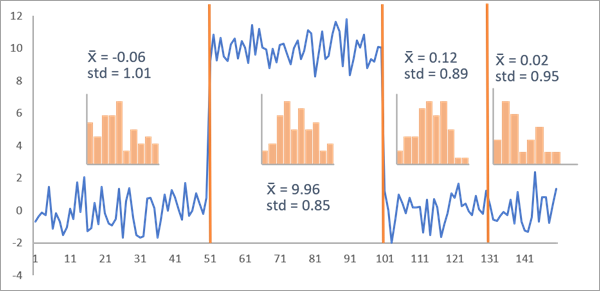
Si aucune contrainte n’est appliquée au nombre de points de changement, l’ajout de points de changement supplémentaires fera toujours baisser le coût de la segmentation. Pour éviter que tous les intervalles temporels soient détectés en tant que points de changement, vous devez utiliser le paramètre Method (Méthode) pour appliquer l’un des deux types de contrainte.

Utilisez l’option Defined number of change points (SegNeigh)(Nombre défini de points de changement [SegNeigh]) pour spécifier le nombre de points de changement à détecter avec le paramètre Number of Change Points (Nombre de points de changement. Cette option utilise l’algorithme Segment Neighborhood (SegNeigh, Auger 1989) pour trouver la segmentation au coût le plus faible parmi toutes les segmentations possibles ayant le nombre de points de changement spécifié.

L’option Auto-detect number of change points (PELT) (Détecter automatiquement le nombre de points de changement [PELT]) utilise l’algorithme Pruned Exact Linear Time (PELT, Killick 2012) pour estimer le nombre de points de changement et leur emplacement. Cet algorithme pénalise l’inclusion de chaque point de changement supplémentaire en ajoutant une valeur de pénalité au coût de chaque segment et trouve la segmentation dont le coût pénalisé (coût de la segmentation plus pénalité) est le plus faible parmi toutes les segmentations possibles. L’algorithme PELT repose sur l’idée qu'un intervalle temporel est détecté en tant que point de changement s’il induit une baisse du coût de la segmentation supérieure à la valeur de pénalité qui lui est ajoutée. Si la baisse du coût est inférieure à la pénalité ajoutée, le coût pénalisé augmente et l’intervalle temporel n’est pas détecté en tant que point de changement.

La valeur de pénalité choisie est déterminante pour les résultats de l’algorithme PELT. Si les pénalités sont trop faibles, de nombreux faux points de changement risquent d’être détectés, et si elles sont trop fortes, de véritables points de changement risquent de ne pas être détectés. La valeur de pénalité utilisée dans l’algorithme PELT est déterminée par la valeur du paramètre Detection Sensitivity (Sensibilité de la détection). La sensibilité est fournie sous la forme d’un nombre compris entre 0 et 1. Les sensibilités élevées permettent de détecter plus de points de changement que des valeurs de pénalité faibles. Chaque emplacement du cube spatio-temporel utilise la même valeur de pénalité à la détection des points de changement.

Pour un changement de moyenne, d’écart type ou de décompte, la valeur de pénalité est calculée à partir de la sensibilité à l’aide de la formule suivante, où n est le nombre d’intervalles temporels de la série chronologique :

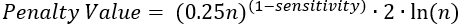
La sensibilité la plus forte, d’une valeur de 1, revient à minimiser le critère d’information bayésien (BIC).

Pour les changements de pente (tendance linéaire), une formule de pénalité plus classique est utilisée :

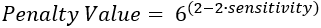
La sensibilité par défaut, d’une valeur de 0,5, revient à minimiser le critère d’information d’Akaike (AIC). Les changements de pente (tendance linéaire) utilise une formule de pénalité plus classique, car les autres types de changement ont des difficultés à différencier les tendances des points de changement. Ils ont donc besoin de valeurs de pénalité plus élevées pour éviter de détecter un trop grand nombre de points de changement. Toutefois, les changements de pente (tendance linéaire) sont conçus pour les données avec des tendances et ne nécessitent pas de valeurs de pénalité aussi importantes.

PELT et SegNeigh sont tous deux des algorithmes récursifs exacts : ils renvoient toujours la segmentation dont le coût est globalement le plus faible, pour une valeur de pénalité ou un nombre de points de changement donnés. Les algorithmes sont exécutés de manière indépendante sur tous les emplacements du cube spatio-temporel en entrée.

Il existe une relation entre les algorithmes PELT et SegNeigh : les deux méthodes détectent les mêmes intervalles temporels en tant que points de changement si elles détectent le même nombre de points de changement. Par exemple, si vous exécutez l’algorithme PELT avec une valeur de pénalité permettant de détecter six points de changement à un emplacement, puis que vous exécutez l’algorithme SegNeigh en spécifiant qu’il y a six points de changement à détecter, les deux méthodes détectent les mêmes intervalles temporels en tant que points de changement.

Longueur minimale de segment

Vous pouvez utiliser le paramètre Longueur minimale de segment pour spécifier le nombre minimal d’intervalles temporels au sein de chaque segment. Si, par exemple, vous disposez de recettes commerciales et spécifiez une longueur minimale de segment égale à 7, chaque point de changement sera séparé d’au moins une semaine. La valeur par défaut de la longueur minimale de segment correspond à la plus faible valeur de calcul du coût du segment. Pour un changement de la moyenne, de l'écart type et du total, la valeur par défaut est de 1, ce qui signifie que chacun des intervalles temporels peut être un point de changement. Pour un changement de pente (tendance linéaire), la valeur par défaut est de 2, car au moins deux intervalles temporels sont requis pour tracer une ligne ajustée aux valeurs du segment.

La longueur minimale de segment est une contrainte supplémentaire eu égard de la contrainte appliquée à l’aide du paramètre Méthode. PELT ou SegNeigh trouve l’ensemble de points de changement ayant le coût de segmentation le plus faible parmi toutes les segmentations possibles dont les segments ont chacun au moins la longueur minimale.

Pratiques conseillées et limitations

Vous devez tenir compte de plusieurs points lors du choix des paramètres et des options de cet outil.

• Les méthodes de détection des points de changement sont classées comme étant en ligne ou hors connexion, tandis que l’outil effectue une détection hors connexion. Les méthodes hors connexion supposent qu’il existe une série chronologique avec un début et une fin. Leur but est de déterminer rétrospectivement quand les changements se sont produits. À l’inverse, les méthodes en ligne sont constamment exécutées sur les données, qui sont mises à jour à mesure que de nouvelles valeurs sont disponibles. L’objectif des méthodes en ligne est la détection en temps réel de nouveaux changements aussi rapidement que possible après qu’ils se soient produits. Les méthodes en ligne et hors connexion diffèrent considérablement dans leurs algorithmes, leurs cas d’utilisation et leurs hypothèses concernant les données.
• Détecter les changements de la moyenne, de l’écart type ou de total est plus efficace sur les données sans tendances, où les changements se produisent dans un seul intervalle temporel. Si la série chronologique comporte des tendances, plusieurs intervalles temporels risquent d’être détectés en tant que points de changement, étant donné que la valeur moyenne change constamment. De même, si le changement est plus graduel et que plusieurs intervalles temporels s’écoulent avant que la valeur change complètement, tous les intervalles temporels inclus dans cette transition risquent d’être détectés en tant que points de changement. Dans ces cas-là, il est recommandé de définir le paramètre Sensibilité de la détection sur des valeurs faibles ou de détecter les changements de pente (tendance linéaire).
• La détection des points de changement est similaire à la détection des points aberrants des séries chronologiques, mais s’en démarque de plusieurs façons importantes. La détection des points de changement permet d’identifier les intervalles temporels où un modèle se transforme en un nouveau modèle (comme dans un changement de valeur moyenne), tandis que la détection des points aberrants permet d’identifier les intervalles temporels qui s’écartent significativement d’un modèle donné. Le premier cas suppose un changement durable, alors que le second suppose une anomalie de courte durée.

• Pour les variables d’analyse représentant des totaux, l’option Total du paramètre Type de changement est souvent la plus appropriée pour détecter les changements dans la valeur moyenne des totaux. Toutefois, l’option Décalage moyen peut fournir des résultats équivalents ou meilleurs pour des données de total. En effet, le modèle du type de changement de total considère que les valeurs de chaque segment suivent une distribution Poisson dans laquelle la variance du segment est égale à sa valeur moyenne. Comme le type de changement de décalage moyen considère à la place que les valeurs de chaque segment sont normalement distribuées, la valeur moyenne peut être supérieure ou inférieure à la variance des valeurs.

  Dans une distribution Poisson, la plupart des totaux se trouvent à environ moins de deux racines carrées de la valeur moyenne. Par exemple, pour une distribution Poisson dont la valeur moyenne est égale à 100, environ 95 % des totaux sont compris entre 80 et 120 (2 × sqrt(100) = 20). Pour une distribution Poisson dont la moyenne est égale à 1 million, la plupart des totaux se situent à entre 998 000 et 1 002 000 (la racine carée de 1 est égale à 1 000). La plage de totaux est comparativement plus étroite pour la moyenne supérieure de 1 million dans laquelle la plupart des totaux se trouvent à moins de 0,2 % de la valeur moyenne. Toutefois, dans la moyenne plus petite de 100, les totaux varient de jusqu’à 20 % de la valeur moyenne. Par rapport à leur valeur moyenne, si les valeurs des totaux varient plus qu’attendu d’une distribution Poisson, de nombreux intervalles temporels peuvent être détectés en tant que points de changement. Il s’agit d’un scénario courant avec les totaux élevés. Dans ce cas, il est recommandé de détecter le décalage moyen.

• Dans tous les types de changement, le premier intervalle temporel n’est jamais détecté en tant que point de changement. Ceci est dû au fait que chaque point de changement marque le début d’un nouveau segment, à compter du deuxième segment. Le premier intervalle temporel étant toujours dans le premier segment, il ne peut jamais être un point de changement. De plus, pour un changement de pente (tendance linéaire), les deux premiers intervalles temporels ne sont jamais détectés comme des points de changement, car le premier segment doit inclure au moins deux intervalles temporels.
• Avec l’option Defined number of change points (SegNeigh) (Nombre défini de points de changement [SegNeigh]) du paramètre Method (Méthode), la segmentation optimale n’est pas toujours unique. Si plusieurs segmentations affichent le même coût, les points de changement optimaux les plus récents sont renvoyés. Par exemple, si toutes les valeurs d’une série chronologique sont égales à un emplacement donné, toutes les segmentations ont la même vraisemblance et le même coût. Dans ce cas, si trois points de changement sont nécessaires, les trois derniers intervalles de temps sont détectés en tant que points de changement à cet emplacement.
• Pour détecter le décalage moyen, il est nécessaire d’estimer la variance des données autour de la moyenne, sans connaître à l’avance les intervalles temporels où un décalage de la moyenne se produit (les points de changement). Les formules de variance classiques étant biaisées en présence d’une moyenne variable inconnue, la formule de variance robuste suivante est utilisée :

  

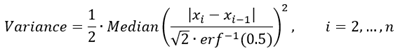
  Pour détecter le changement de pente, il est également nécessaire d’estimer une variance inconnue autour d’une ligne de tendance ; la formule de variance robuste suivante est utilisée :

  

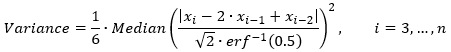
  Si le résultat de l’une des formules est zéro, la variance est estimée en supposant qu’il n’y a pas de décalage ni de tendance de la valeur moyenne.

Ressources supplémentaires

Pour plus d’informations sur la détection des points de changement, consultez les références suivantes :

• I.E. Auger et C.E. Lawrence, (1989). « Algorithms for the optimal identification of segment neighborhoods. »Bulletin of Mathematical Biology. 51(1):39-54. https://doi.org/10.1007/BF02458835
• R. Killick, P. Fearnhead et I.A. Eckley, (2012). « Optimal Detection of Changepoints With a Linear Computational Cost. » Journal of the American Statistical Association. 107. 1590-1598. https://dx.doi.org/10.1080/01621459.2012.737745
• R. Killick et I.A. Eckley, (2014). « changepoint: An R Package for Changepoint Analysis. » Journal of Statistical Software. https://dx.doi.org/10.18637/jss.v058.i03